2.8.2. Гіпербола

Означення. Гіперболою називають геометричне місце точок площини, для яких модуль різниці відстаней від двох фіксованих точок цієї самої площини, що звуться фокусами, є величиною сталою.

Позначимо фокуси гіперболи через і ,а відстань між ними – через 2с (Рис. 2.23). Введемо на площині прямокутну систему координат. За вісь Ох візьмемо пряму, що проходить крізь фокуси та з додатним напрямом від до , а вісь Оу проведемо через середину відрізка перпендикулярно до осі Ох (Рис. 2.23).

y

L₁ B₂ L₂

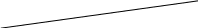M

F₁ A₁ O A₂ F₂ x

K₁ B₁ K₂

Рис. 2.23

Тоді координати фокусів гіперболи відносно цієї системи будуть , . Позначимо через довільну точку гіперболи і назвемо відрізки і (а також їх довжини і ) фокальними радіусами цієї точки. Модуль різниці відстаней між фокусами позначимо через 2а.

З випливає, що різниця , звідси отримуємо , або . Ця нерівність є умовою існування гіперболи.

Відстані від точки М до та відповідно становлять

За означенням точка М лежить на гіперболі тоді і лише тоді, коли

,

тобто

.

Отже,

. (35)

Це і є рівняння гіперболи. Спростимо його. Запишемо рівняння (35) так

Піднесемо обидві частини цього рівняння до квадрата

,

або

Піднісши до квадрата обидві частини цієї рівності, матимемо

Звідки

(36)

Оскільки , то величина додатна. Нехай . Тоді рівняння (36) набуває вигляду

або

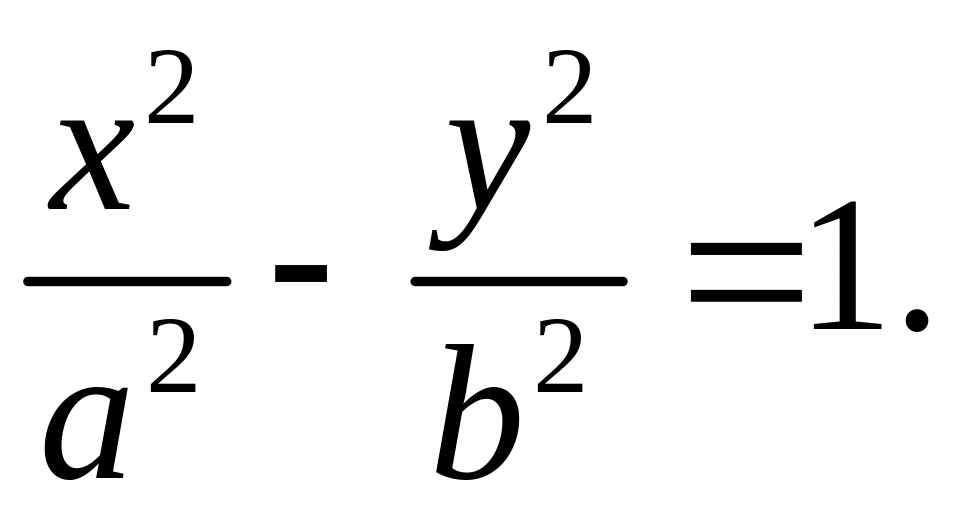(37)

Можна довести, що незважаючи на двократне піднесення до степеня рівняння (37), яке при цьому отримується, є еквівалентним рівнянню (35). Тобто рівняння (37) є рівнянням гіперболи, означеної на початку підрозділу. Рівняння (37) отримало назву канонічне рівняння гіперболи.

Дослідимо форму гіперболи за допомогою рівняння (37). Оскільки це рівняння не змінюється при заміні х на (–х) і у на (–у), то гіпербола симетрична відносно осей Ох і Оу. Тому достатньо розглянути лише ту частину гіперболи, яка лежить у першому квадранті. Нехай і . Тоді з рівняння (37) дістанемо

, (38)

звідки , при матимемо . Тоді з рівняння (38) випливає, що при необмеженому зростанні х від а до значення у збільшується. Отже, гіпербола – необмежена крива.

Розглянемо пряму , рівняння якої

. (39)

Покажемо, що гіпербола у першому квадранті координатної площини Оху як завгодно близько наближається до прямої (39). Нехай – точка гіперболи, а – точка прямої, яка має однакову з М абсцису х (Рис. 2.24).

у

у

О а х х

Рис. 2.24

Розглянемо відстань

(40)

З (40) випливає, що при знаменник дробу у правій частині рівності (40) необмежено зростає, а тому . Отже, точка необмежено наближається до прямої при .

Означення. Якщо К – деяка необмежена крива, і точка М, переміщуючись по цій кривій у нескінченість, необмежено наближається до прямої , то пряму називають асимптотою кривої К.

Отже, пряма , яка має рівняння (39), є асимптотою тієї гілки гіперболи (37), яка розташована в першому квадранті координатної площини Оху .

Всю гіперболу дістанемо за допомогою симетричних відображень відносно осей Ох і Оу. Гіпербола має дві асимптоти, що є діагоналями прямокутника сторони якого дорівнюють і (Рис. 2.23). Точки А₁ і А₂ називають вершинами гіперболи, а відрізки і (а також їх довжини і ) – осями гіперболи.

53