Конспект лекцій з навчальної дисципліни

“Лінійна алгебра та аналітична геометрія”.

Розділ 1. Лінійна алгебра

1.1. Матриці та їх властивості

Розглянемо систему трьох лінійних алгебраїчних рів­нянь з трьома невідомими х,y,z:

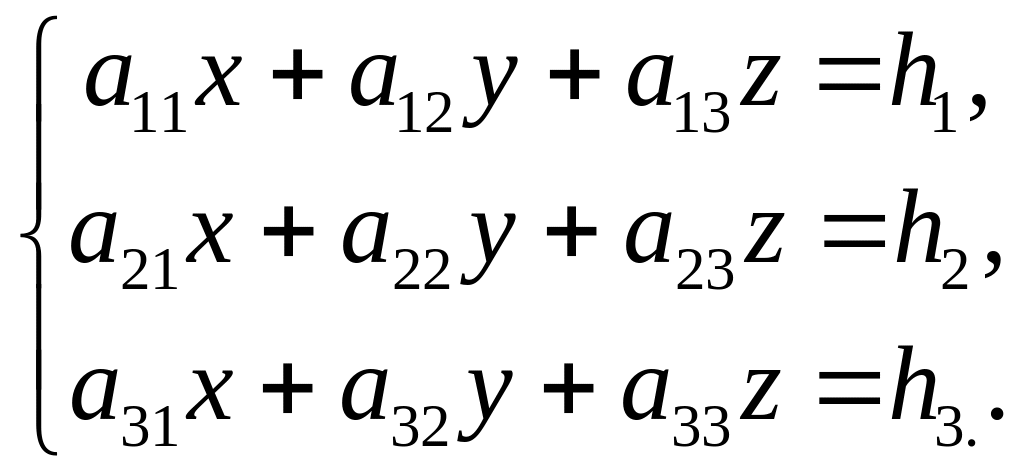(1.1)

Усі коефіцієнти а (їх дев'ять) та вільні члени h (їх три) вважаємо заданими.

Таблиця, яка складена з коефіцієнтів а при невідомих х, у і z системи (1.1) і записана у вигляді

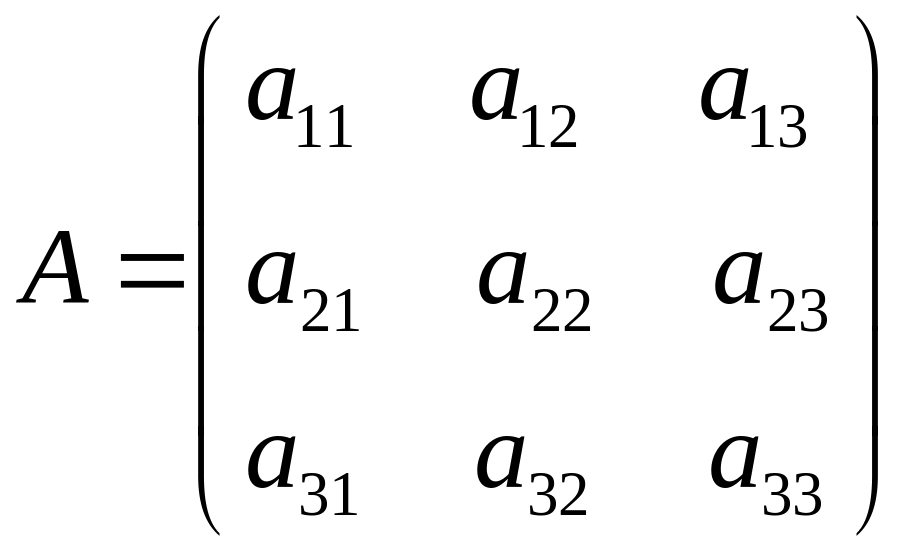, або (1.2)

називається матрицею А. –елементи цієї матриці, вони утворюють рядки (і- номер рядка) та стовпчики (j- номер стовпчика). Елементи матриці називаються діагональними ( вони розташовані на головній діагоналі). Якщо , тоді така матриця називається прямокутною. У випадку, коли , така матриця називається квадратною п- го порядку. Наприклад, матриця (1.2) є третього порядку. Якщо і=1, а j>1 (або j=1, a i>1), тоді отримуємо матрицю – рядок (а₁ а₂ ... а_п) (або матрицю – стовпчик ), яка називається вектор – рядок ( або вектор - стовпчик).

Дві матриці А=(а_ij) і В=(b_ij) рівні, якщо рівні між собою їх відповідні елементи а_ij=b_ij. Якщо а_ij=а_jі тоді матриця А називається симетричною.

Матриці можна поелементно додавати, перемножувати на число.

Добутком матриці на матрицю називається матриця , у якої елемент дорівнює сумі добутків елементів і-того рядка матриці А і -го стовпчика матриці В, тобто:

. (1.3)

Приклад 1. Дано і В=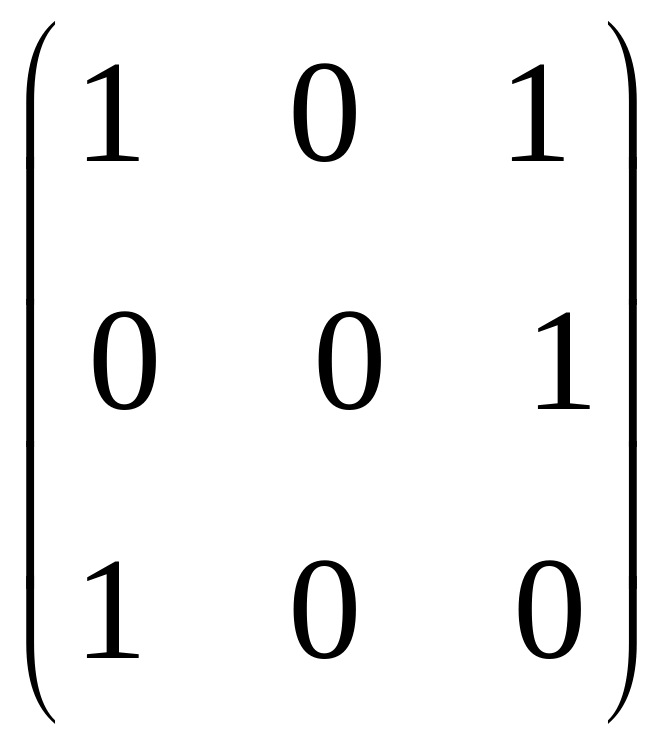 . Обчислити .

.

Приклад 2. Дано і . Обчислити і .

і .

Як бачимо, , тобто в загальному випадку для добутку двох матриць властивість перестановки не є характерною.

Матриця, в якої елементи на головній діагоналі дорівнюють одиниці

( ), а усі інші елементи дорівнюють нулю, називається одиничною матрицею:

. (1.4)

Для будь-якої матриці А справедлива така властивість:

. (1.5)

1.2. Визначники та їх властивості

З поняттям квадратної матриці тісно пов'язане поняття ви­значника. Наприклад, визначником третього порядку, який відпові­дає матриці А (1.2), називається число, яке позначають символом

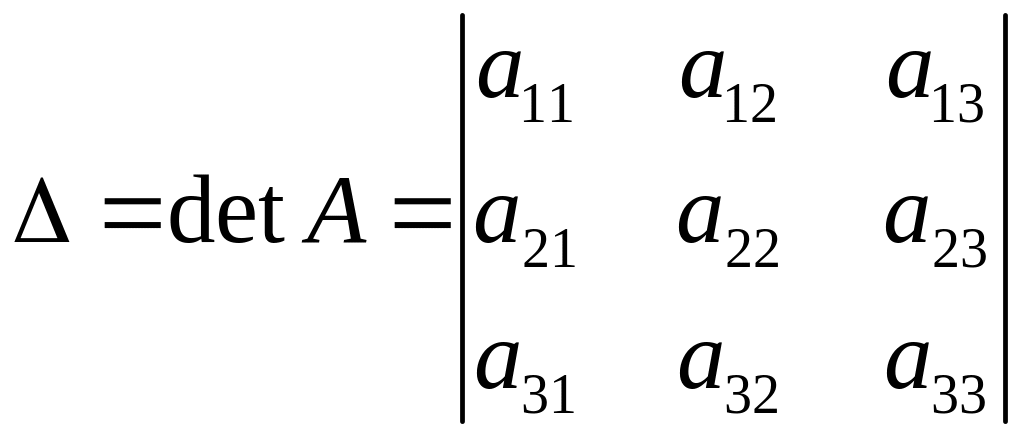(1.6)

і визначають за таким правилом

(1.7)

при фіксованому номері рядка і;

тут - мінор елемента визначника (1.6).

Мінором деякого елемента визначника називається визначник, який отримують з даного визначника шляхом викреслювання рядка і стовпчика, на перетині яких розташований цей елемент. Наприклад, мінором елемента визначника (1.6) є визначник другого порядку

Величину при фіксованих значеннях і та j назива­ють алгебраїчним доповненням елемента а_ij визначника.

Визначник другого порядку обчислюється (розкривається) за та­ким правилом:

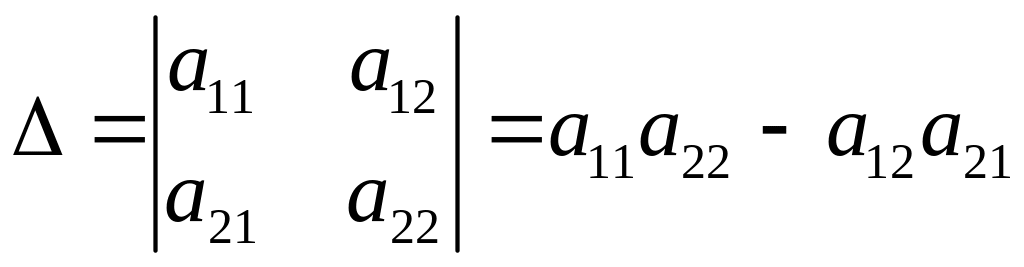. (1.8)

Приклад 1. Обчислити .

Розкриваємо визначник, наприклад, за першим рядком. За формулами (1.7) і (1.8) маємо:

.

Розглянемо основні властивості визначника:

1. Величина визначника не зміниться, якщо його рядкики і стовпчики поміняти місцями.

2. Якщо переставити два рядки (чи два стовпчики) визначника, тоді це рівносильне помноженню його на –1.

3. Якщо визначник містить два однакові рядки (чи два стовпчики), тоді він дорівнює нулю.

4. Перемноження усіх елементів одного рядка (чи одного стовпчика) визначника на будь-яке число рівносильне добутку визначника на це число.

Звідси, якщо:

1. елементи двох рядків (чи двох стовпчиків) визначника про­ порційні, то визначник, згідно з властивістю 3, дорівнює нулю;

2. усі елементи деякого рядка (чи стовпчика) дорівнюють нулю, то і сам визначник теж дорівнює нулю;

3. до елементів деякого рядка (чи стовпчика) визначника додати відповідні елементи іншого рядка (чи стовпчика), перемножені на будь-який спільний множник, то величина визначника не зміниться.

Приклад 2.