1.5. Диференціальні рівняння другого порядку. Деякі типи.

З звичайних диференціальних рівнянь другого порядку вище першого найширше застування в науці і техніці мають рівняння другого порядку.

Символічно звичайне диференціальне рівняння другого порядку можна записати у вигляді

, (22)

або у вигляді, розв’язаному відносно другої похідної,

. (23)

Як і для рівнянь першого порядку, будемо звати розв’язком рівняння (22) або (23), якщо підставлення у (22) або (23) перетворює його на тотожність. Відшукання такої функції і становить задачу інтегрування диференціального рівняння другого порядку.

Задаючи початкові умови

,

можна знайти єдиний розв’язок рівняння (23) у деякій області (задача Коші), якщо функція та її частинні похідні і визначенні та неперервні у цій області (за теоремою Коші).

Розглянемо окремі типи рівнянь другого порядку, інтегрування яких зводиться, як і розглянутих досі рівнянь першого порядку, до відшукання невизначених інтегралів.

1.5.1. Тип перший . Розв’язок такого рівняння знаходиться шляхом двох послідовних інтеграцій.

Приклад 7. Зінтегрувати рівняння

.

Інтегруючи, дістанемо

.

Звідси

,

а тому друга інтеграція дає

1.5.2. Тип другий . Заміною дане рівняння зводиться до рівняння першого порядку з відокремлюваними змінними.

Приклад 8. Зінтегрувати рівняння

.

Покладемо

,

отже,

.

Після такої заміни дане рівняння стає

.

Відокремлюючи змінні та інтегруючи, дістанемо

.

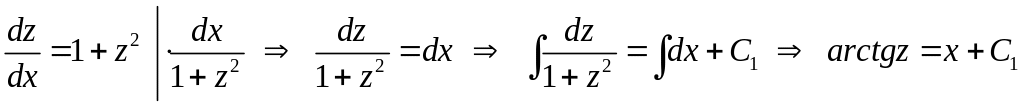Звідси або

.

Відокремлюючи змінні та інтегруючи вдруге, матимемо

.

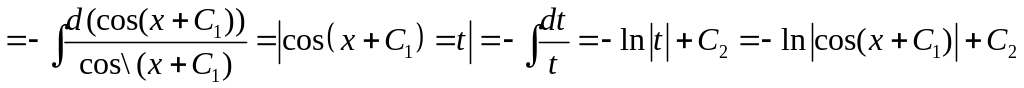1.6. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами

Рівняння виду

, (24)

де і – неперервні функції, називається лінійним диференціальним рівнянням другого порядку.

Загальний розв’язок рівняння (24) є сума його будь-якого частинного розв’язку і загального розв’язку відповідного однорідного рівняння ( за ) (за теоремою).

Якщо функції і – сталі величини, тоді рівняння (24) називається лінійним рівнянням другого порядку зі сталими коефіцієнтами.

Розглянемо лінійне однорідне рівняння другого порядку зі сталими коефіцієнтами

. (25)

Рівняння

(26)

називається характеристичним рівнянням диференціального рівняння (25).

За теоремою:

1) якщо корені характеристичного рівняння дійсні (26) та різні ( ), тоді загальний розв’язок рівняння (25) має вигляд:

(27)

2) якщо корені характеристичного рівняння (26) дійсні та рівні між собою ( ), тоді загальний розв’язок рівняння (25) має вигляд:

(28)

3) якщо корені характеристичного рівняння (26) не дійсні, а комплексно спряжені ( і ), тоді загальний розв’язок рівняння (25) має вигляд:

. (29)

Зауваження. Комплексним числом z називається впорядкована пара дійсних чисел (х;у) на площині Оху, тобто . При цьому х називається дійсною, а у – уявною частинами комплексного числа z. Комплексне число z можна представити в алгебраїчній формі так:

(30)

де – уявна одиниця.

Комплексне число називається комплексно спряженим числу Справедлива формула Ейлера:

Приклад 2. Знайти розв’язок рівняння .

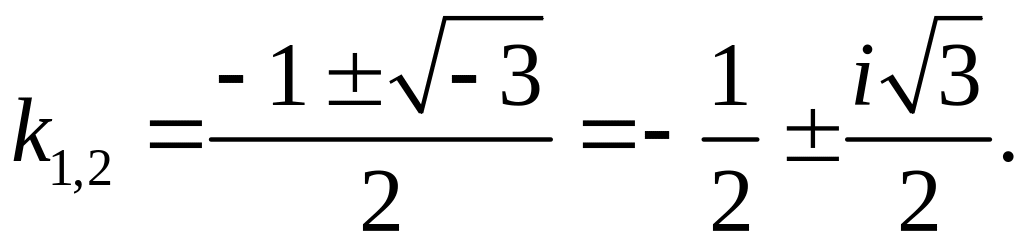Характеристичне рівняння має такий вигляд: Його корені дорівнюють: Тоді загальний розв’язок рівняння буде: