Конспект лекцій з вищої математики

Р о з д і л : „Диференціальні рівняння”

1. Звичайні диференціальні рівняння

1.1. Основні означення

Різноманітні геометричні, фізичні, технічні та іншого характеру задачі часто приводять до рівнянь, які крім незалежних змінних і невідомих функцій містять ще й похідні цих функцій.

Означення. Нетотожне співвідношення між змінними та їх похідними (або диференціалами) зветься диференціальним рівнянням.

Якщо шукана функція залежить від одного аргументу, то диференціальне рівняння зветься звичайним. Лише такі рівняння і будемо вивчати у першому розділі.

Символічно звичайне диференціальне рівняння можна записати у вигляді

(1)

В (1) х − незалежна змінна, − шукана функція, − звичайні похідні від функції першого, другого і п-го порядку відповідно.

Порядок найвищої похідної, яку містить дане диференціальне рівняння, звуть порядком цього рівняння.

Отже,

є звичайне диференціальне рівняння першого порядку, а

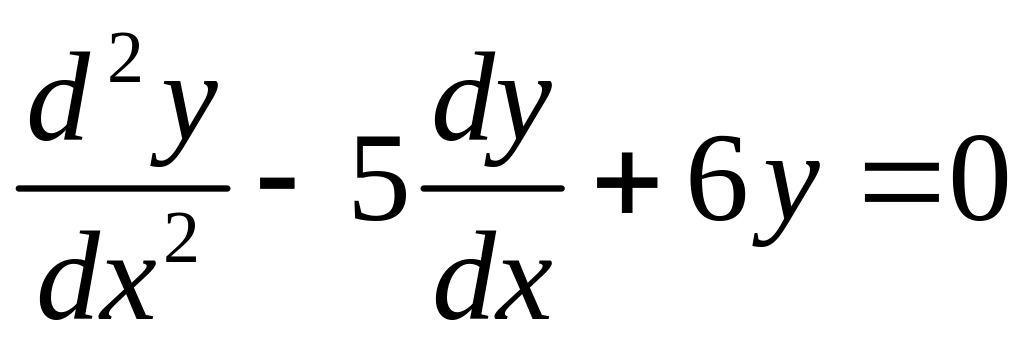
є теж звичайне диференціальне рівняння, але другого порядку.

Означення. Розв’язком диференціального рівняння (1) зветься кожна функція , яка, будучи підставлена в рівняння, перетворює його на тотожність.

Процес відшукання таких функцій зветься інтегруванням диференціальних рівнянь.

1.2. Диференціальні рівняння першого порядку

Загальний вигляд диференціального рівняння першого порядку

Якщо його розв’язати відносно , то воно матиме вигляд

(2)

Тільки такі рівняння, тобто рівняння у вигляді (2), ми і будемо вивчати у цьому підрозділі.

Приклад 1. Показати, що функція є розв’язком диференціального рівняння

(3)

Справді, , отже підставлення функції дає тотожність

Легко перевірити також, що функція , де С − довільна стала, також є розв’язком рівняння (3). Цей розв’язок називається загальним розв’язком рівняння (3). При С = 0 з нього можна отримати розв’язок Більше того, залежно від значення С ми отримуємо з загального розв’язку цілий набір частинних розв’язків.

Задаючи, наприклад, таку початкову умову

, (4 )

де і − задані числа, можна отримати будь-який частинний розв’язок диференціального рівняння (3). Для цього знайдемо довільну сталу С у загальному розв’язку :

У результаті отримуємо частинний розв’язок рівняння (3)

який задовольняє умову (4).

Знайти єдиний розв’язок рівняння (2), який задовольняє початкову умову (4), − це одна з найважливіших задач теорії диференціальних рівнянь. Ця задача називається задачею Коші. Доведено, що задача (2), (4) має єдиний розв’язок, коли функція неперервна в області розв’язання задачі і має обмежену похідну в цій області (теорема Коші).

Функцію завжди можна подати у вигляді частки двох відомих функцій

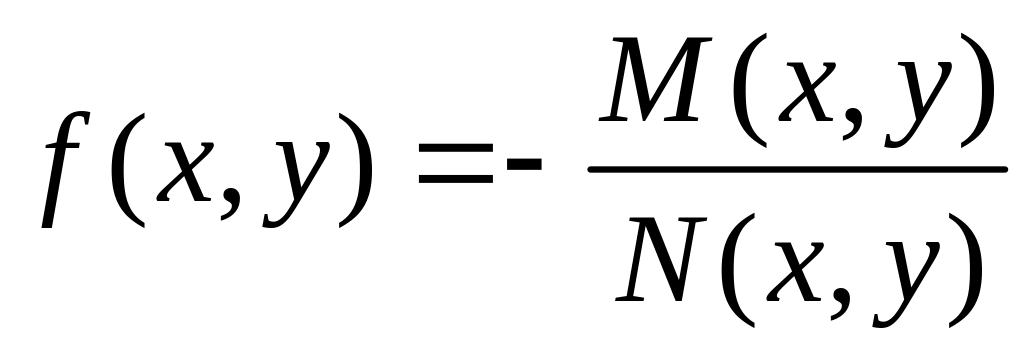
і записати рівняння (2) у такий спосіб

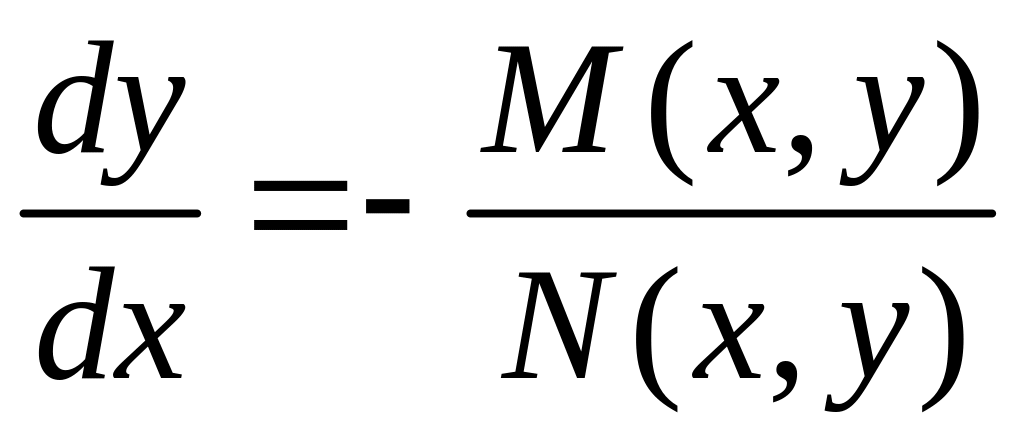
або

Ця форма запису дає співвідношення між змінними х, у та їх диференціалами. Вона зручна тим, що тут х та у рівноправні, тобто кожну з них можна розглядати як функцію другої.

Далі розглянемо деякі типи рівнянь першого порядку і для кожного з них викладемо притаманні способи їх інтегрування.

1.3. Звичайні диференціальні рівняння з відокремлюваними змінними

Рівняння

(5)

де та − відомі неперервні функції своїх аргументів, зветься диференціальним рівнянням з відокремлeними змінними. (При стоїть функція тільки від х, а при − функція тільки від у). Для розв’язання рівняння (5) досить його зінтегрувати почленно:

(6)

тут С − довільна стала.

Співвідношення (6) звуть загальним інтегралом рівняння (5); воно подає у як неявну функцію від х. Якщо можливо, то розв’язуємо (6) відносно у, і тоді матимемо загальний розв’язок рівняння (4).

Приклад 2. Зінтегрувати рівняння

Маємо

Позначивши 2С₁ = С дістанемо остаточно

Рівняння

зветься диференціальним рівнянням з відокремлюваними змінними. Воно легко зводиться до рівняння (5). Для цього досить обидві його частини поділимо на вираз . Зробивши це, після очевидних скорочень матимемо

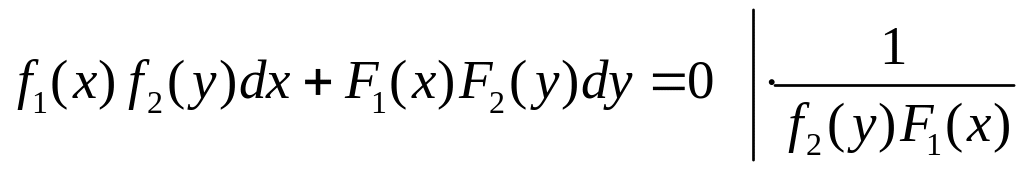
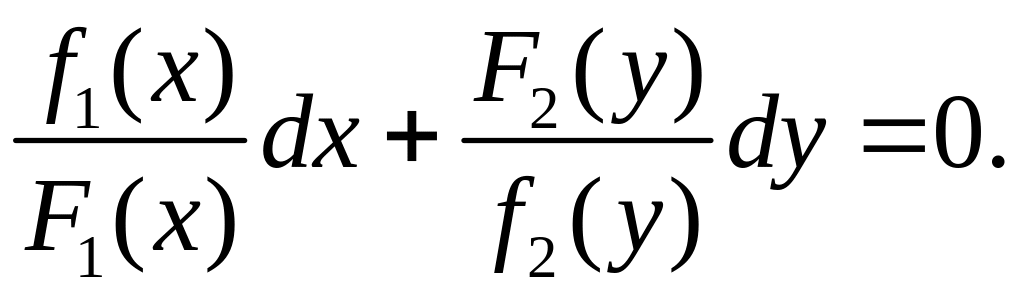
Одержане рівняння є рівнянням з відокремленими змінними. Зінтегрувавши почленно

,

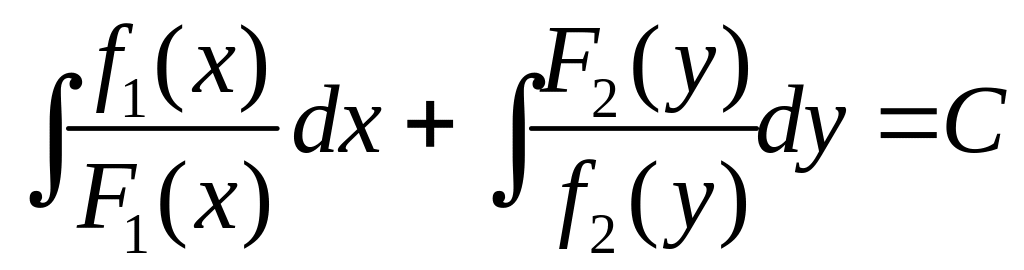отримаємо його загальний інтеграл.

Приклад 3. Зінтегрувати рівняння

(7)

Поділимо рівняння (7) на і дістанемо рівняння з відокремленими змінними

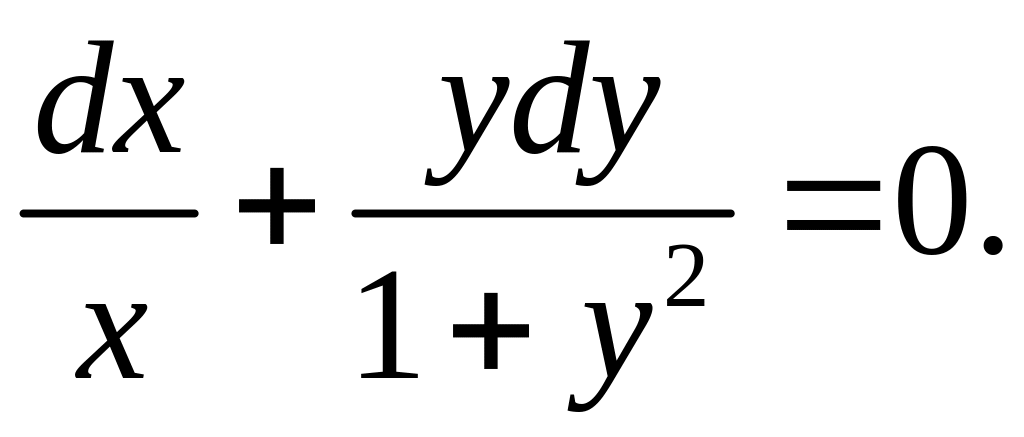
Звідси

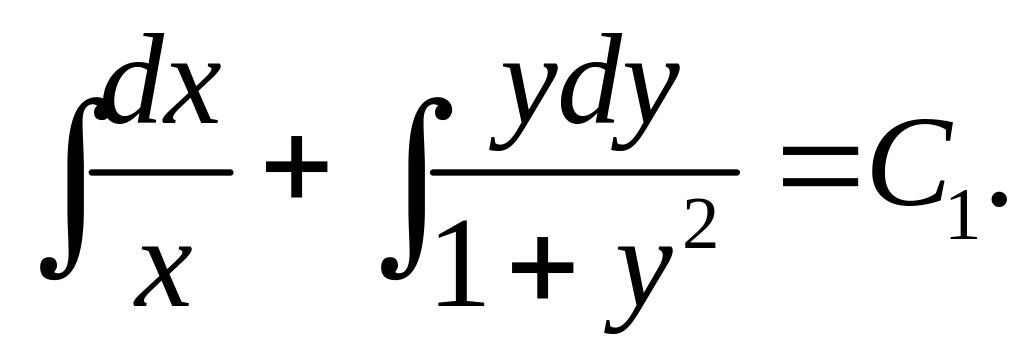(8)

Але

а другий інтеграл обчислюється так

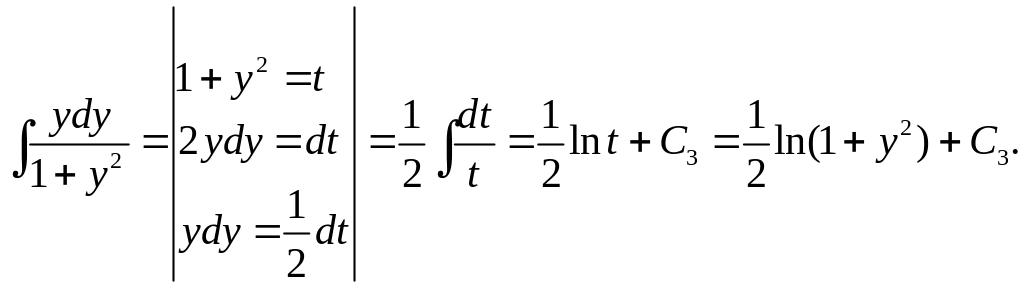
Підставимо одержані значення інтегралів у (8)

Тут Одержаний загальний інтеграл можна спростити:

Поклавши де С − нова довільна стала, пропотенціюємо одержаний вираз

,

і остаточно дістанемо загальний інтеграл рівняння (7)

Приклад 4. Розв’язати рівняння за умови

Використаємо для позначення Лейбніца Тоді рівняння, яке слід розв’язати, набирає вигляду

Помножимо обидві частини цього рівняння на при цьому отримаємо

Це рівняння з відокремленими змінними. Зінтегруємо його

Розв’яжемо це рівняння відносно у:

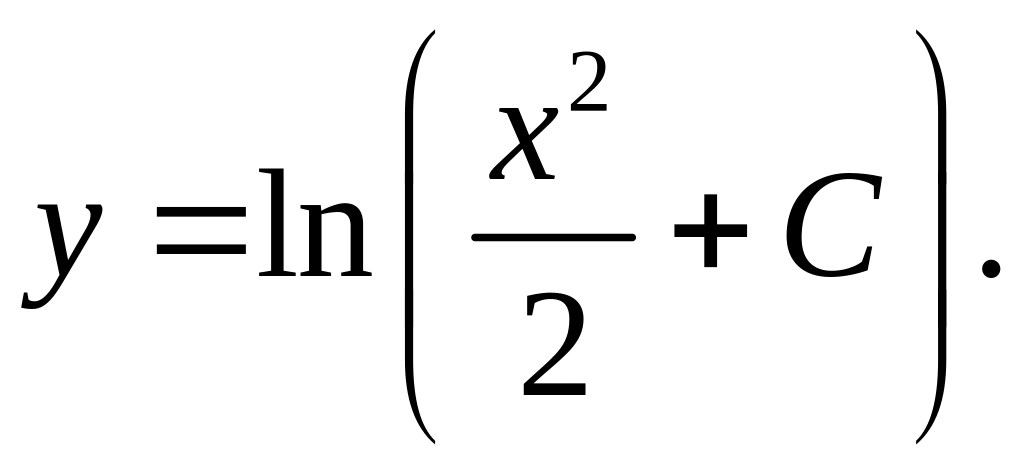
З початкової умови визначимо сталу С :

Шуканий розв’язок тоді, остаточно, буде