Раздел 5. Протоколы идентификации с нулевым разглашением. Задание к лабораторной работе №5: «Протоколы идентификации с нулевым разглашением».

Разработать программу, в которой был бы реализован один из следующих протоколов идентификации с нулевым разглашением:

Вариант 1: Фиата-Шамира.

Вариант 2: Файге-Фиата-Шамира.

Вариант 3: Шнорра.

Вариант 4: Гиллу-Кискате.

Вариант 5: Окамото.

Использовать класс больших чисел, разработанный ранее.

В схемах Фиата-Шамира, Файге-Фиата-Шамира, Гиллу-Кискате простые числа p и q генерировать с помощью вероятностного теста на простоту.

В схемах Шнорра и Окамото простые числа p и q должны быть доказуемо простыми. Необходимо генерировать сначала число q с помощью алгоритма генерации доказуемо простых чисел, потом формировать число p=2rq+1, r=1,2,… и проверять его на простоту. Если оно получилось составным, то формируем следующее число и проверяем, и так до тех пор пока не найдем простое. Также числа p и q можно сгенерировать процедурой ГОСТ 34.11-94.

В схеме Гиллу-Кискате число b нужно генерировать вероятностным тестом на простоту и проверять условие НОД(b,φ(n))=1.

Данные для самопроверки к разделу 5.

Схема идентификации Фиата-Шамира.

1. Задать значение параметров p, q, t в из табл. 5.1;

2. проверить правильность вычисления v₁…v_k, подставив параметры s₁…s_k из табл. 5.1;

3. проверить правильность вычисления x, подставив r из табл. 5.1;

4. проверить правильность вычисления y, подставив e из табл. 5.1;

5. сравнение 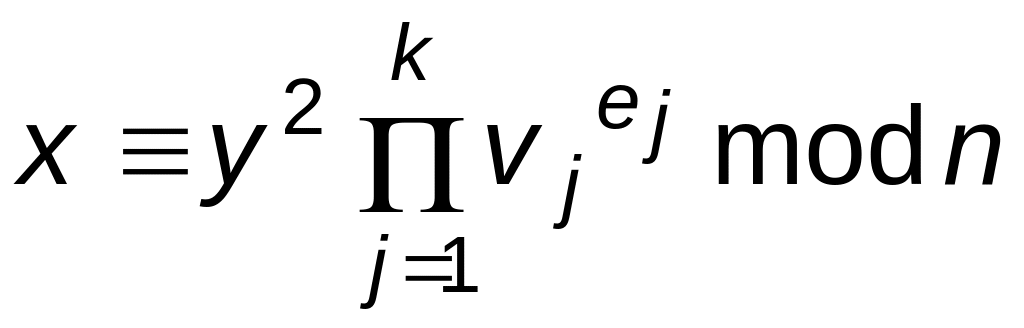должно быть верным.

Таблица 5.1

№	p	q	t	s1…sk	v1…vk	r	x	e	y
1	5	13	2	(48,34,40)	(9,51,25)	60	25	(0,0,0)	25
2	11	41	3	(267,357,267)	(291,125,291)	39	168	(1,0,1)	168
3	13	37	2	(446,362,389)	(139,270,300)	286	26	(1,0,1)	286
4	23	19	2	(337,6)	(277,85)	295	62	(1,0)	216
5	29	31	4	(800,254,56)	(521,335,428)	185	63	(1,0,1)	119
6	43	11	2	(111,113,453)	(144,236,311)	448	152	(0,0,0)	448
7	23	47	5	(142,101,77)	(565,71,262)	538	817	(0,0,1)	817
8	11	29	3	(138,210,18)	(103,45,64)	223	284	(0,0,1)	284
9	17	7	3	(104,64,88)	(64,50,53)	3	9	(0,1,0)	73
10	29	37	4	(1003,413)	(1043,480)	346	613	(0,1)	189

Схема идентификации Файге-Фиата-Шамира.

1. Задать значение параметров p, q, t из табл. 5.2;

2. проверить правильность вычисления l₁…l_k, подставив s₁…s_k из табл. 5.2;

3. проверить правильность вычисления x, подставив r из табл. 5.2;

4. проверить правильность вычисления y, подставив e из табл. 5.2;

5. одно из сравнений или 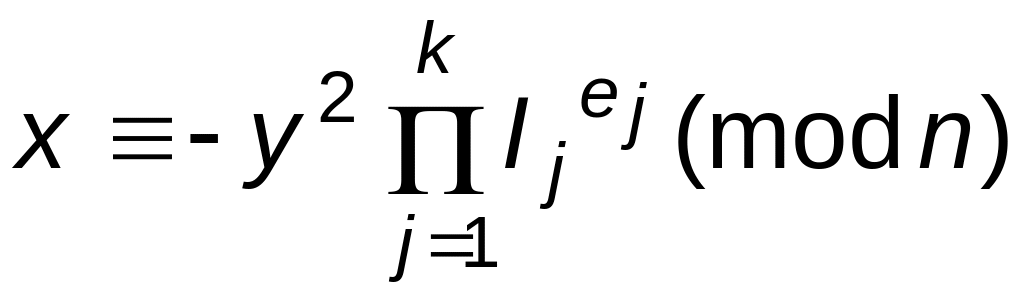должно быть верным.

Таблица 5.2

№	p	q	s1…sk	l1…lj	t	r	x	e	y
1	111	107	(182,133,88)	(6841,1630,9963)	1	6	36	(1,0,1)	7086
2	103	131	(123,111,96)	(2532,449,3893)	1	2	13489	(0,0,0)	2
3	115	107	(132,196,163)	(1649,6919,201)	1	68	8869	(1,0,0)	8364
4	111	107	(199,170,97)	(3599,7351,2950)	1	77	5948	(1,0,0)	3446
5	127	115	(167,48)	(9276,14231)	1	45	2025	(0,0)	45
6	151	103	(8,108)	(243,5183)	2	33	14464	(1,0)	264
7	107	167	(182,152,165)	(6971,4748,6889)	3	72	12685	(1,1,1)	6627
8	131	187	(32,65)	(8062,1838)	1	25	23872	(0,1)	1625
9	123	195	(146,38,181)	(4664,4601,7606)	3	55	20960	(0,1,0)	2090
10	119	127	(33,54,46)	(1818,4877,3364)	4	39	13592	(1,0,0)	1287

Схема идентификации Шнорра.

1. Задать значения параметров p, q, t из табл. 5.3;

2. проверить правильность вычисления g, a, v по табл. 5.3;

3. проверить правильность вычисления x, подставив r из табл. 5.3;

4. проверить правильность вычисления y, подставив e из табл. 5.3;

5. сравнение x≡α^yv^e (mod p) должно быть верным.

Таблица 5.3

№	p	q	g	a	t	s	v	r	x	e	y
1	709	59	2	551	4	9	104	11	540	15	28
2	1087	181	3	729	5	49	55	15	277	9	94
3	599	23	7	103	4	6	384	17	384	14	9
4	2609	163	3	830	6	60	242	34	2376	42	109
5	977	61	3	101	3	14	835	4	131	5	13
6	1213	101	2	457	4	51	398	20	464	11	76
7	1559	41	19	1490	3	7	546	9	240	6	10
8	1811	181	6	508	6	150	1755	178	1372	11	18
9	2213	79	2	769	5	31	1685	65	1956	18	70
10	439	73	15	331	4	61	252	14	223	7	3

Схема идентификации Гиллу-Кискате.

1. Задать значения параметров p, q, b из табл. 5.4;

2. проверить правильность вычисления v, подставив u из табл. 5.4;

3. проверить правильность вычисления x, подставив r из табл. 5.4;

4. проверить правильность вычисления y, подставив e из табл. 5.4;

5. сравнение x≡y^bv^e (mod n) должно быть верным.

Таблица 5.4

№	p	q	b	u	v	r	x	e	y
1	47	67	139	751	2772	216	263	50	3083
2	59	83	53	3874	2579	1191	4574	4	266
3	101	79	149	4754	2619	4245	7339	130	927
4	107	59	113	5179	871	5187	4585	36	4775
5	97	109	79	7459	1611	6432	6541	15	9902
6	89	29	61	185	2550	1914	1189	57	1363
7	71	31	139	212	1277	173	1901	16	741
8	61	59	37	1731	3139	3495	246	20	445
9	97	71	29	3830	3856	2792	804	19	3295
10	43	79	19	2481	1379	2117	1244	7	3080

Теперь следует проверить корректность схемы (то есть, опознается ли в ней нарушитель). Задать значения u и v из таблицы 5.5, при этом u и v не соответствуют друг другу. В результате протокола доказывающий не должен пройти идентификацию.

Таблица 5.5

№	p	q	b	u	v
1	47	67	139	751	2579
2	59	83	53	3874	2619
3	101	79	149	4754	927
4	107	59	113	5179	2550
5	97	109	79	7459	1277
6	89	29	61	185	1363
7	71	31	139	212	3495
8	61	59	37	1731	2792
9	97	71	29	3830	3295
10	43	79	19	2481	3080

Схема идентификации Окамото.

1. Задать значения p, q, t, a₁ из табл. 5.6;

2. проверить правильность вычисления v, подставив a₁, a₂, s₁ и s₂ из табл. 5.6;

3. проверить правильность вычисления x, подставив r₁ и r₂ из табл. 5.6;

4. проверить правильность вычисления y₁ и y₂, подставив e из табл. 5.6;

5. сравнение x≡α₁^y1α₂^y2v^e (mod p) должно быть верным.

Таблица 5.6

№	p	q	t	a1	a2	s1	s2	v	x	r1	r2	e	y1	y2
1	1754881	457	4	6	4	11	10	66146	921762	17	17	5	72	67
2	5463401	463	4	24	19	2	7	4094343	4911269	11	6	12	35	90
3	8483749	457	4	22	11	12	1	185435	6503340	20	2	10	140	12
4	13175299	487	4	7	24	16	19	9190147	7479831	10	7	12	202	235
5	6858767	211	4	11	14	19	10	3570017	3940065	7	20	8	159	100
6	6433181	227	4	22	4	12	15	5728611	2854688	18	8	13	174	203
7	6568697	241	4	6	2	2	15	947550	6431550	19	19	13	45	214
8	3619477	271	4	5	7	12	17	85725	1134962	9	5	4	57	73
9	2790217	271	4	20	11	8	7	276674	1348232	18	13	8	82	69
10	3778889	281	4	3	1	14	16	2726270	2187	7	21	15	217	261

Теперь следует проверить корректность схемы (то есть, опознается ли в ней нарушитель). Задать значениe v из таблицы 5.7, при этом a₁, a₂, s₁, s₂ и v не соответствуют друг другу. В результате протокола доказывающий не должен пройти идентификацию.

Таблица 5.7

№	p	q	t	a1	a2	s1	s2	v
1	1754881	457	4	6	4	11	10	76136
2	5463401	463	4	24	19	2	7	904543
3	8483749	457	4	22	11	12	1	795425
4	13175299	487	4	7	24	16	19	195137
5	6858767	211	4	11	14	19	10	6599017
6	6433181	227	4	22	4	12	15	592611
7	6568697	241	4	6	2	2	15	747080
8	3619477	271	4	5	7	12	17	29026
9	2790217	271	4	20	11	8	7	175479
10	3778889	281	4	3	1	14	16	9520224