Приложения

Приложение 1. Решение сравнения относительно неизвестного y.

В процедуре восстановления тайного сообщения в протоколе скрытого канала подписи Онга-Шнорра-Шамира нам необходимо решить сравнение относительно y:

s₂y=(x - s₁r) mod (p-1).

Данное сравнение может иметь несколько решений. Решать его следует следующим образом:

1. t=(x - s₁r); n=НОД(s₂,p-1);

2. , , ;

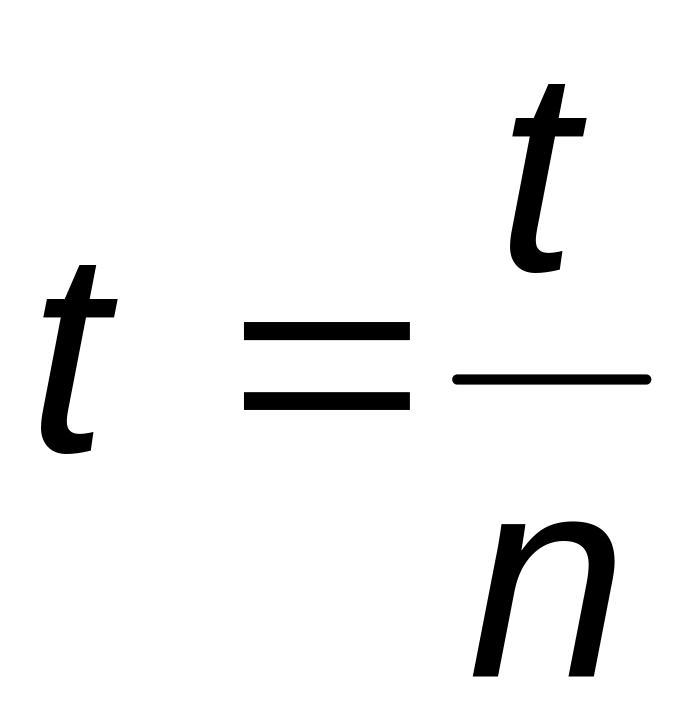3. y=(s₂^-1∙t) mod p_n;

4. Возникают n вариантов тайного сообщения, одно из которых верное:

y₁ mod (p-1);

(y₁+p_n) mod (p-1);

………

(y₁+(n-1)p_n) mod (p-1).

Сообщение которое является осмысленным, как раз и является верным. Оно должно выбираться человеком или проверкой осмысленности по словарю.

Приложение 2. Процедура генерации S-блоков алгоритма шифрования ГОСТ 28147-89 к тестовым данным для протокола подбрасывания монеты на основе симметричной криптосистемы.

procedure TGOST.GreateSBlocks;

var i,j:integer;

const

s1:array[0..15]of byte=(4,10,9,3,13,8,0,14,6,11,1,12,7,15,5,2);

s2:array[0..15]of byte=(4,10,9,2,13,8,0,14,6,11,1,12,7,15,5,3);

begin

for i:=0 to 15 do

SBlock[0,i]:=s1[i];

for j:=1 to 7 do

for i:=0 to 15 do

SBlock[j,i]:=s2[i];

end;

Приложение 3. S-блоки для шифрования ГОСТ 28147-89 к тестовым данным для протокола Yahalom.

SBlock: Array[0..7] of Array[0..15] of Integer =

((4, 10, 9, 2, 13, 8, 0, 14, 6, 11, 1, 12, 7, 15, 5, 3),

(14, 11, 4, 12, 6, 13, 15, 10, 2, 3, 8, 1, 0, 7, 5, 9),

(5, 8, 1, 13, 10, 3, 4, 2, 14, 15, 12, 7, 6, 0, 9, 11),

(7, 13, 10, 1, 0, 8, 9, 15, 14, 4, 6, 12, 11, 2, 5, 3),

(6, 12, 7, 1, 5, 15, 13, 8, 4, 10, 9, 14, 0, 3, 11, 2),

(4, 11, 10, 0, 7, 2, 1, 13, 3, 6, 8, 5, 9, 12, 15, 14),

(13, 11, 4, 1, 3, 15, 5, 9, 0, 10, 14, 7, 6, 8, 2, 12),

(1, 15, 13, 0, 5, 7, 10, 4 ,9, 2, 3, 14, 6, 11, 8, 12));

Приложение 4. Процедура генерации S-блоков алгоритма шифрования ГОСТ 28147-89 к тестовым данным для протокола Нидхема-Шредера.

procedure TGOST.GenerateSBlocks;

begin

SBlock[0]:='4A93D80E6B1C7F52';

SBlock[1]:='4A92D80E6B1C7F53';

SBlock[2]:='4A92D80E6B1C7F53';

SBlock[3]:='4A92D80E6B1C7F53';

SBlock[4]:='4A92D80E6B1C7F53';

SBlock[5]:='4A92D80E6B1C7F53';

SBlock[6]:='4A92D80E6B1C7F53';

SBlock[7]:='4A92D80E6B1C7F53';

end;

СПИСОК ЛИТЕРАТУРЫ

1. Шнайер Б., Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. – М.: ТРИУМФ, 2003. – 816 с.

2. Молдовян А.А., Молдовян Н.А. Введение в криптосистемы с открытым ключом. – СПб.: БХВ-Петербург, 2005. – 288 с.

3. Ниссенбаум О.В. Криптографические протоколы: учеб. пособие/ О. В. Ниссенбаум. - Тюмень: Изд-во ТюмГУ, 2007, - 116 c.

4. Информационные технологии на основе модулярной алгебры/ О. Д. Жуков-Емельянов. - Москва: Красанд, 2010. - 248 с.

5. Рябко Б.Я., Фионов А.Н. Криптографические методы защиты информации: Учебное пособие для вузов. – М.: Горячая линия – Телеком, 2005. – 229 с.

6. A. Menezes, P. van Oorschort, S. Vanstone, Handbook of Applied Cryptography – CRC Press, Inc., 5th edition, 2001

http://cacr.uwaterloo.ca/hac/

7. Анохин М.И., Варновский Н.П., Сидельников В.М., Ященко В.В. Криптография в банковском деле.

http://geo.com.ru/db/msg.html?mid=1161287&uri=all.html

Ольга Владимировна Ниссенбаум Николай Владимирович Поляков

КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ

Лабораторный практикум

Учебно-методическое пособие

для студентов специальностей

«Компьютерная безопасность» и «Информационная безопасность автоматизированных систем»