Задача д7

Применение к исследованию движения механической системы уравнений Лагранжа второго рода с одной степенью свободы

Данная задача на применение к изучению движения системы уравнений Лагранжа второго рода. В задачах система имеет одну степень свободы, поэтому ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение.

Выбор обобщенной координаты определяется искомой величиной, то есть если требуется определить угловое ускорение некоторого тела, то за обобщенную координату принимают угол поворота этого тела , где - номер тела, если требуется определить линейное ускорение тела, то за обобщенную координату принимают перемещение х соответствующего тела, то есть . Далее следует вычислить кинетическую энергию системы T, выразив все входящие в нее переменные величины через обобщенную координату и обобщенную скорость .

Затем необходимо вычислить обобщенную силу. Для этого следует сообщить системе возможное малое перемещение, при котором обобщенная координата получает положительное приращение и подсчитать сумму элементарных работ всех сил на этом перемещении. Коэффициент при в полученном выражении и будет обобщенной силой Q.

Пример

Механическая система состоит из ступенчатого блока 3 (радиусы ступеней R₃=R, r₃=0,6R), груза 1 и катков 2,4 с радиусом r_i=0,5R, прикрепленным к концам нитей, намотанных на ступени блока (рис.Д7).

На систему кроме сил тяжести действует сила , приложенная к телу 4 и пара сил сопротивления М, приложенная к блоку 3.

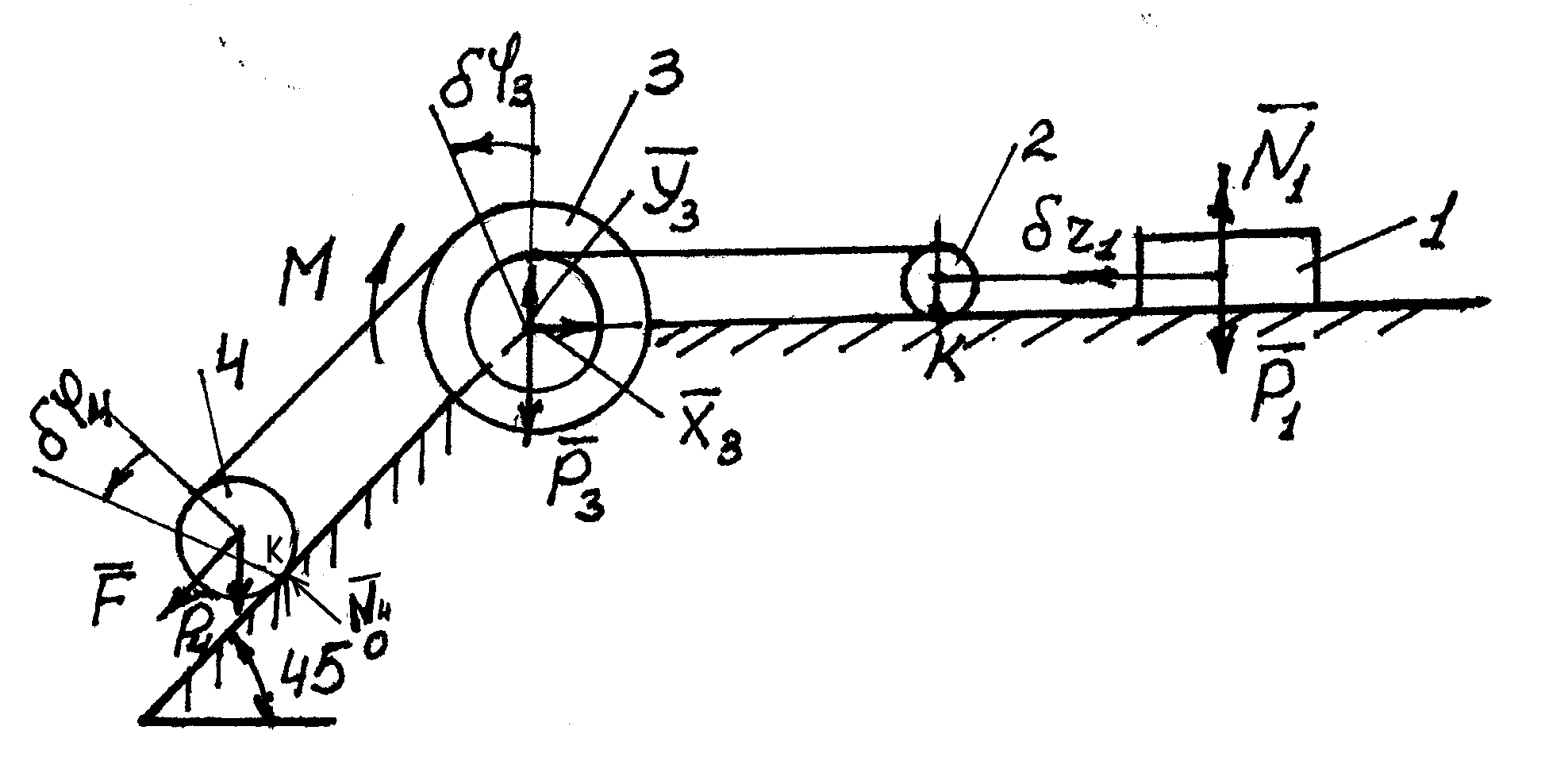
Рис. Д7

Дано: R = 0,3 м, m₁ = 3 кг, m₂= 0 кг, m₃ = 6 кг, m₄= 4 кг, F= 150 Н,

М = 6 Нм

Найти: угловое ускорение блока .

Решение

Система имеет одну степень свободы. Выберем в качестве обобщенной координаты , угол поворота блока 3( рис.Д.7), полагая, что система приходит в движение при перемещении тела 4 вниз.

Составим уравнение Лагранжа

. (1)

2. Определим кинетическую энергию Т системы

Т =Т₁ + Т₂ + Т₃ + Т₄ , (2)

Т₂=0, поскольку m₂=0.

Так как тело 1 движется поступательно, тело 3 вращается вокруг неподвижной оси, а тело 4 - плоскопараллельно, то

Т₁= ; Т₃= ; (3)

Т₄= ,

где, исходя из условия ( см. задание),

; . (4)

3. Все скорости входящие в Т₁, Т₃, Т₄ выразим через обобщенную скорость , равную, очевидно, ₃. Если при этом учесть, что точки К, К являются для тел 2 и 4 мгновенными центрами скоростей соответственно, то получим:

;

; (5)

.

Подставляя значения величин (5) и (4) в равенства (3), а затем значения Т₁, Т₃,Т₄ в равенство (2),найдем окончательно, что

. (6)

Так как здесь Т зависит только от , то

, и . (7)

4. Найдем обобщенную силу Q . Для этого покажем силы, действующие на систему при ее движении(см. рис. Д.7). Затем сообщим системе возможное перемещение, при котором обобщенная координата получит положительное приращение и составим сумму элементарных работ всех сил на этом возможном перемещении

, (8)

где .

Элементарная работа остальных сил равна нулю, так как силы - перпендикулярны возможным перемещениям соответствующих тел, а силы приложены к неподвижной точке.

Учитывая, что линейные и угловые перемещения связаны как и соответствующие скорости, находим

. (9)

Подставляя значение (9), то есть в равенство (8) и вынося за скобки находим, что

. (10)

Коэффициент при в полученном выражении и будет обобщенной силой .

Тогда уравнение (10) примет вид

или . (11)

Необходимо помнить, что размерность обобщенной силы равна размерности работы деленной на размерность соответствующей обобщенной координаты, то есть в данном случае .

5. Подставляя найденные величины (7) и (11) в уравнение (1), получим

0,3 =20,7.

Отсюда находим искомое значение .

Ответ: .