
- •Федеральное агентство железнодорожного транспорта
- •Часть вторая
- •Новикова Вера Николаевна
- •1.Общие указания к выполнению Расчетно-графических работ
- •2. Динамика Задача д1 Динамика материальной точки
- •Интегрируя (19), получаем
- •Интегрируя уравнение (23), получаем
- •Из (27) находим
- •Задача д 2 Динамика относительного движения материальной точки
- •Задача д3 Применение теоремы об изменении кинетического момента системы
- •Учитывая, что , так как другие внешние силы не создают момента относительно оси z, из (1) находим
- •Задача д4 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы
- •С учётом (14) выражение (13) приобретает вид
- •Задача д 5
- •Задача д6
- •Задача д7
- •Библиографический список
Задача д6
Применение принципа возможных перемещений
к определению условий равновесия механической системы
Данная задача на определение условий равновесия механической системы с помощью принципа возможных перемещений.
Принцип
возможных перемещений дает общий метод
решения задач статики. То есть, для
равновесия механической системы с
наложенными на нее геометрическими,
стационарными, удерживающими, идеальными
связями необходимо, чтобы сумма
элементарных работ активных сил системы
на любых возможных перемещениях из
рассматриваемого положения равнялась
нулю:![]() =
=
![]()
![]() = 0, , где
- возможные перемещения точек системы.
= 0, , где
- возможные перемещения точек системы.
Как известно, возможными перемещениями называются воображаемые бесконечно малые перемещения точек и тел механической системы, допускаемые связями, наложенными на систему в данный момент времени.
В рассматриваемой задаче механизм имеет одну степень свободы, т.е. одно независимое перемещение. Для решения задачи необходимо сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар на этом перемещении и приравнять ее нулю. Все вошедшие в составленное уравнение возможные перемещения следует выразить через какое-нибудь одно. Чтобы найти деформацию пружины, надо из полученного уравнения равновесия определить силу упругости . На рис. эту силу можно направить в любую сторону , т.е. считать пружину растянутой (или сжатой); верно ли выбрано направление силы, укажет знак.
Пример
Плоский механизм (рис. Д6,а) состоит из стержней 1,2,3 и ползуна Д, соединенных друг с другом и с неподвижными опорами О, В шарнирами.
К ползуну Д прикреплена пружина с коэффициентом жесткости С, а к стержням 1, 3 пары сил с моментами М1 , М2 , то есть дано:
= 600, = 1200 , j = 900 ,=900 = 00 , = 1200 , 1 = 0,4 м, 3 =0.6 м, АЕ = ЕД,
С = 1,8 104 Н/м, М1 = 150 Нм, М2 =400 Нм.
Определить деформацию Х пружины при равновесии механизма.
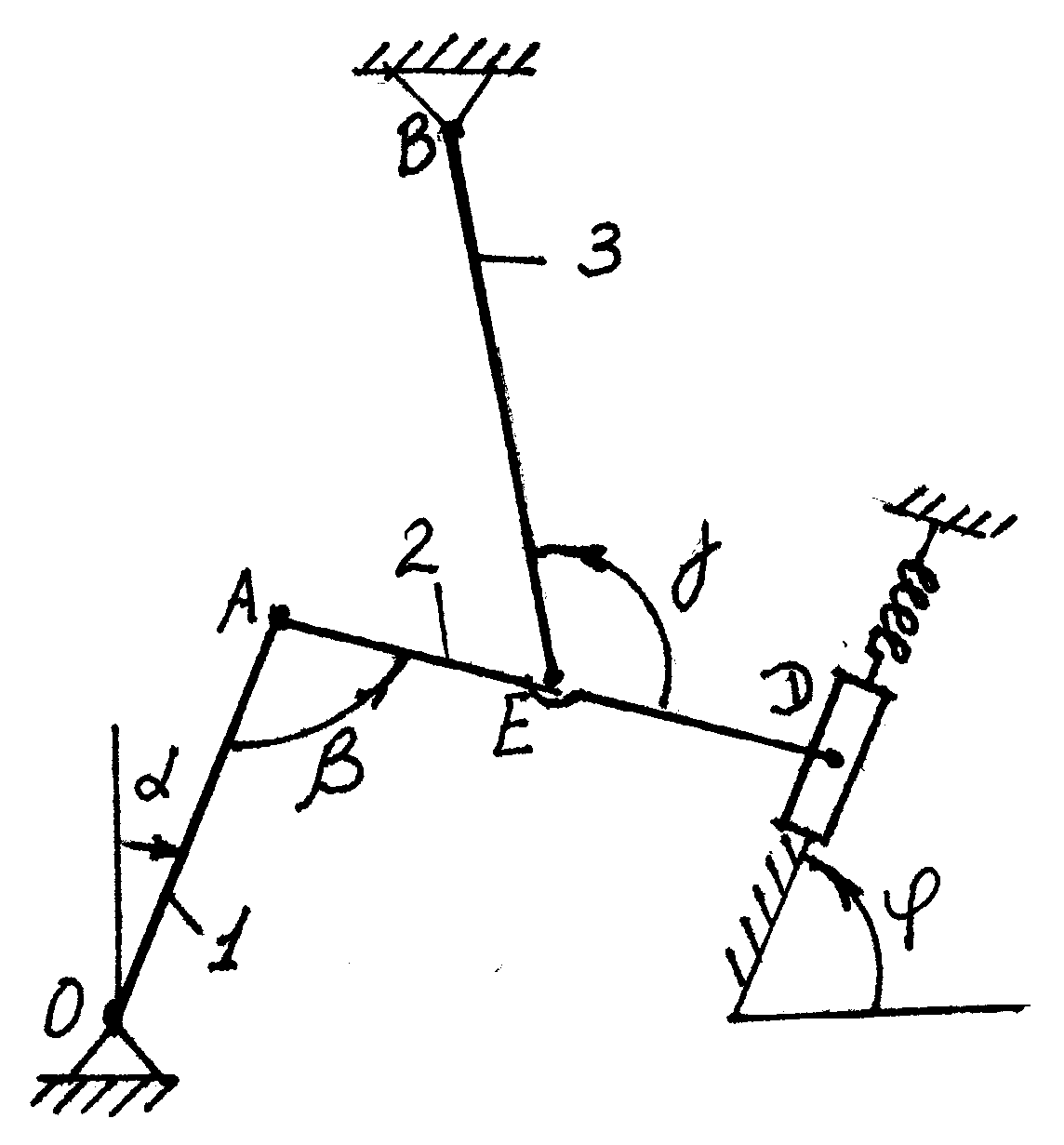
а) б)
Рис Д6
Решение
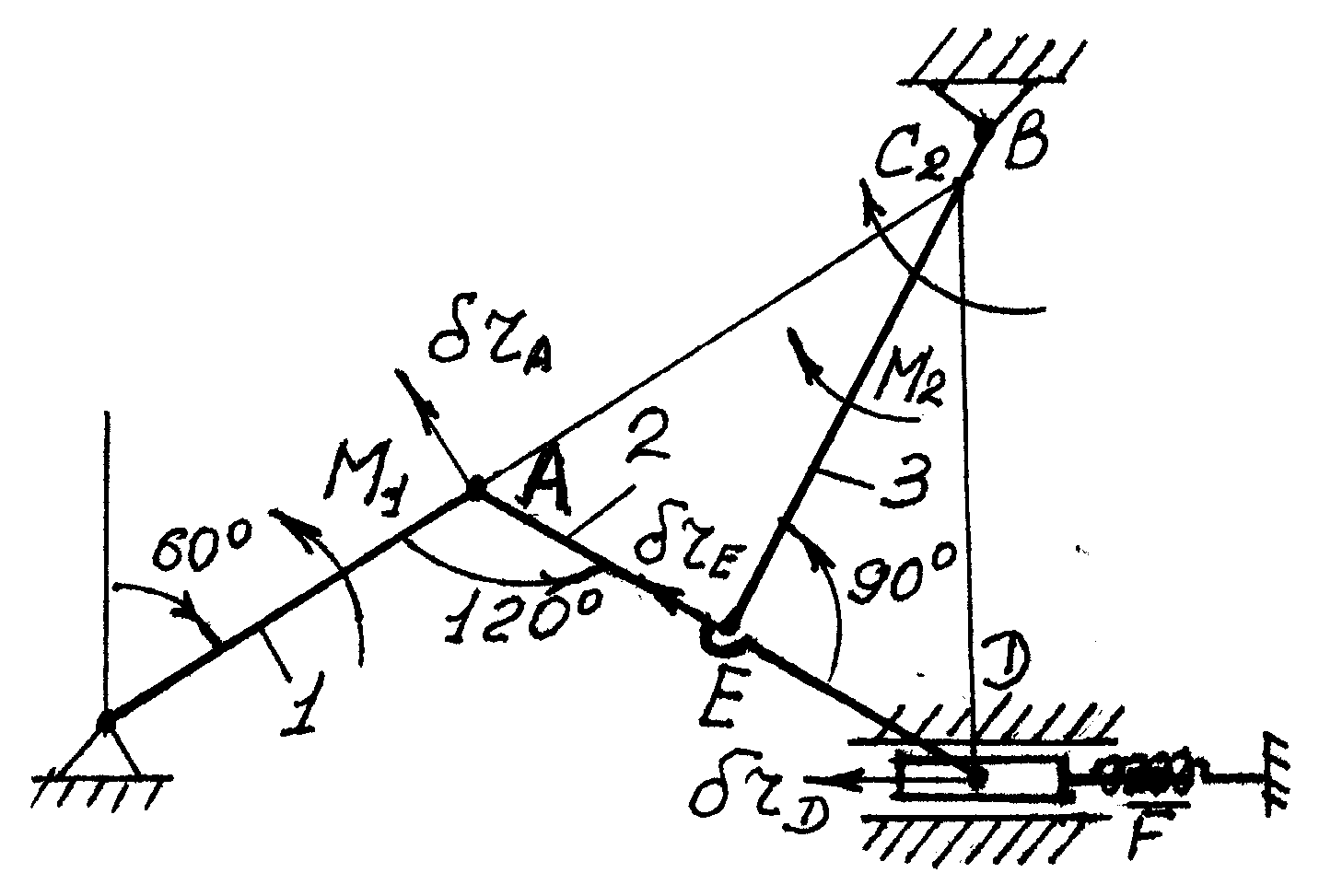
1. Строим положение механизма в соответствии с заданными углами (рис. Д6,б); при этом прикрепляем пружину к ползуну согласно указанию в задании.
Для решения задачи воспользуемся принципом возможных перемещений, то есть
![]() =
0. (1)
=
0. (1)
Изображаем действующие на механизм активные силы: пары с моментами М1 ,М2 и силу упругости пружины, предполагая, что пружина растянута. Неизвестную силу найдем с помощью уравнения (1), а зная и учитывая, что F = cх, определим х.
Чтобы составить уравнение (1), сообщим механизму возможное перемещение и введем следующие обозначения для перемещения звеньев, к которым приложены активные силы: 1 , 3 поворот стержней 1 и 3 соответственно вокруг осей О и В, rД - перемещение ползуна Д. Из перемещений 1, 3, rД - независимое от других одно (у механизма одна степень свободы). Примем за независимое возможное перемещение 1 и установим, какими тогда будут 3 и rД, выразив их через 1. При этом важно определить и направления возможных перемещений, так как иначе в уравнении (1) будут ошибки в знаках.
При расчетах необходимо учесть, что зависимость между возможными перемещениями будет такой же, как и между соответствующими скоростями звеньев механизма при его движении и поэтому воспользуемся известными из кинематики соотношениями.
Сначала найдем и покажем rА (направление rА определяется направлением 1), получим:
rА = 11; rА ОА. (2)
Теперь определим и изобразим rД, учитывая, что проекции rД и rА на прямую АД должны быть равны друг другу, то есть иметь одинаковые модули и знаки. Тогда
rД
cos
300
= rА
cos
300
и rД
= rА
=
![]() 1.
(3)
1.
(3)
Чтобы определить 3 найдем сначала rЕ . Для этого построим мгновенный центр вращения (скоростей) С2 стержня 2 (AD) (на пересечении перпендикуляров к rА и rД, восстановленных из точек А и Д) и покажем направление поворота стержня 2 вокруг С2, учитывая направление rА и rД.
Так как С2 АД = С2ДА = 600 , то АС2Д - равносторонний и С2Е в нем высота, поскольку АЕ = ЕД.
Тогда перемещение rЕ перпендикулярное С2Е будет направлено по прямой АД. При изображении rЕ учитываем направление поворота вокруг центра С2.
Воспользовавшись тем, что проекции rЕ и rА на прямую ЕА должны быть равны друг другу, получим:
rЕ = rА cos 300 = 11 cos 300. (4)
Кроме того
3
=![]() =
=
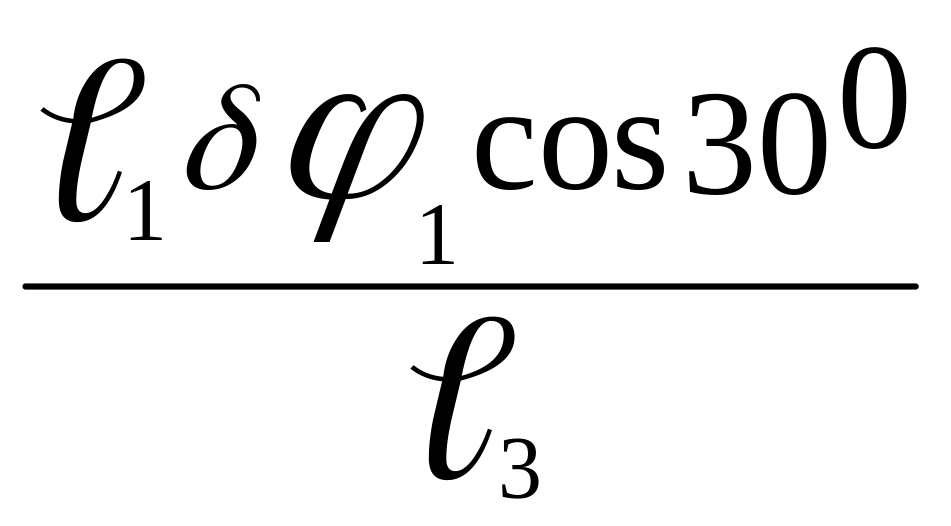 .
(5)
.
(5)
Теперь составляя для механизма уравнение (1), получим:
М11 + М23 FrД = 0. (6)
или заменив rД и 3 их значениями (3) и (5), и вынося 1 за скобки, будем иметь
М11+
М2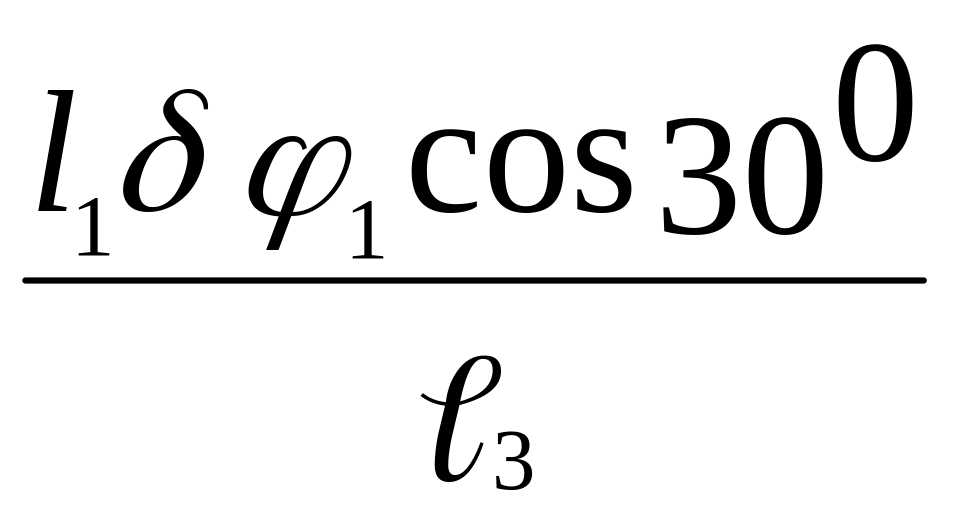
F
F![]() = 0;
= 0;
1
(М1
+ М2
F
F![]() )
= 0.
)
= 0.
Так как 10, то отсюда следует, что
М1
+ М2
F
= 0;
F
= 0;
F
=
![]()
М2
М2 =
=
![]() ;
;
Х
=
![]() .
.
Ответ: Х=530,5 10-4 м.
Знак указывает, что пружина, как и предполагалось, растянута.
