С учётом (14) выражение (13) приобретает вид

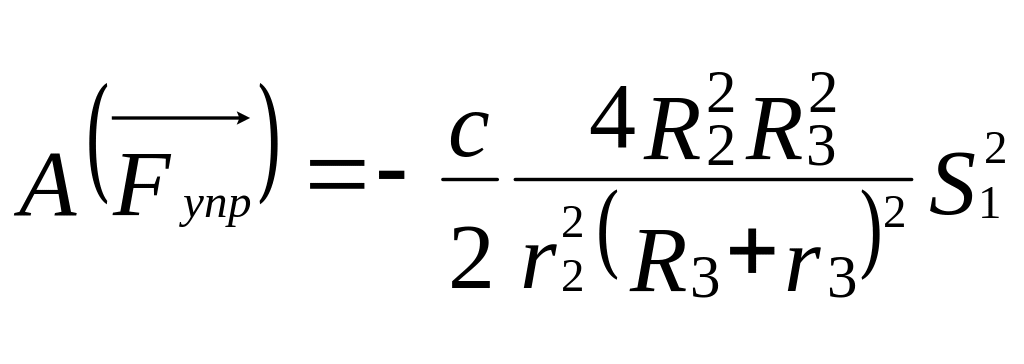. (15)

Суммируя (7), (8), (10), (12) и (15), получаем

. (16)

Приравнивая выражения (6) и (16), находим выражение для искомой величены – ; подставляя в найденное выражение все числовые значения заданных величин, получаем значение .

.

Задача д 5

Применение принципа Даламбера к определению реакций связей

Данная задача на применение к изучению движения системы принципа Даламбера. То есть, если к каждой точке движущейся механической системы приложить соответствующую силу инерции, то действующие на систему силы и силы инерции уравновесятся. При этом в зависимости от характера движения тела систему сил инерции можно заменить или главным вектором сил инерции =  m , или главным моментом сил инерции относительно оси вращения =  J_Z , или обоими инерционными факторами вместе, где: m -масса тела; -ускорение его центра масс; - момент инерции тела относительно оси вращения Z; - угловое ускорение тела.

Необходимо отметить, что линия действия силы в общем случае не проходит через точку С ( см. пример Д5).

Пример

Определить реакции подпятника А и подшипника В вала, вращающего с постоянной угловой скоростью  вокруг вертикальной оси У, если m ₁-масса однородного стержня К N=2l, m₂ - масса груза, закрепленного на конце невесомого стержня l ,  и углы, которые составляют стержни с осью вала. При этом АК=КЕ=ЕД=ДВ=а.

Решение

1.Изображаем ( с учетом заданных углов ) вал и прикрепленные к нему стержни в точках К и Е, а также груз закрепленный в точке М ( рис. Д5).

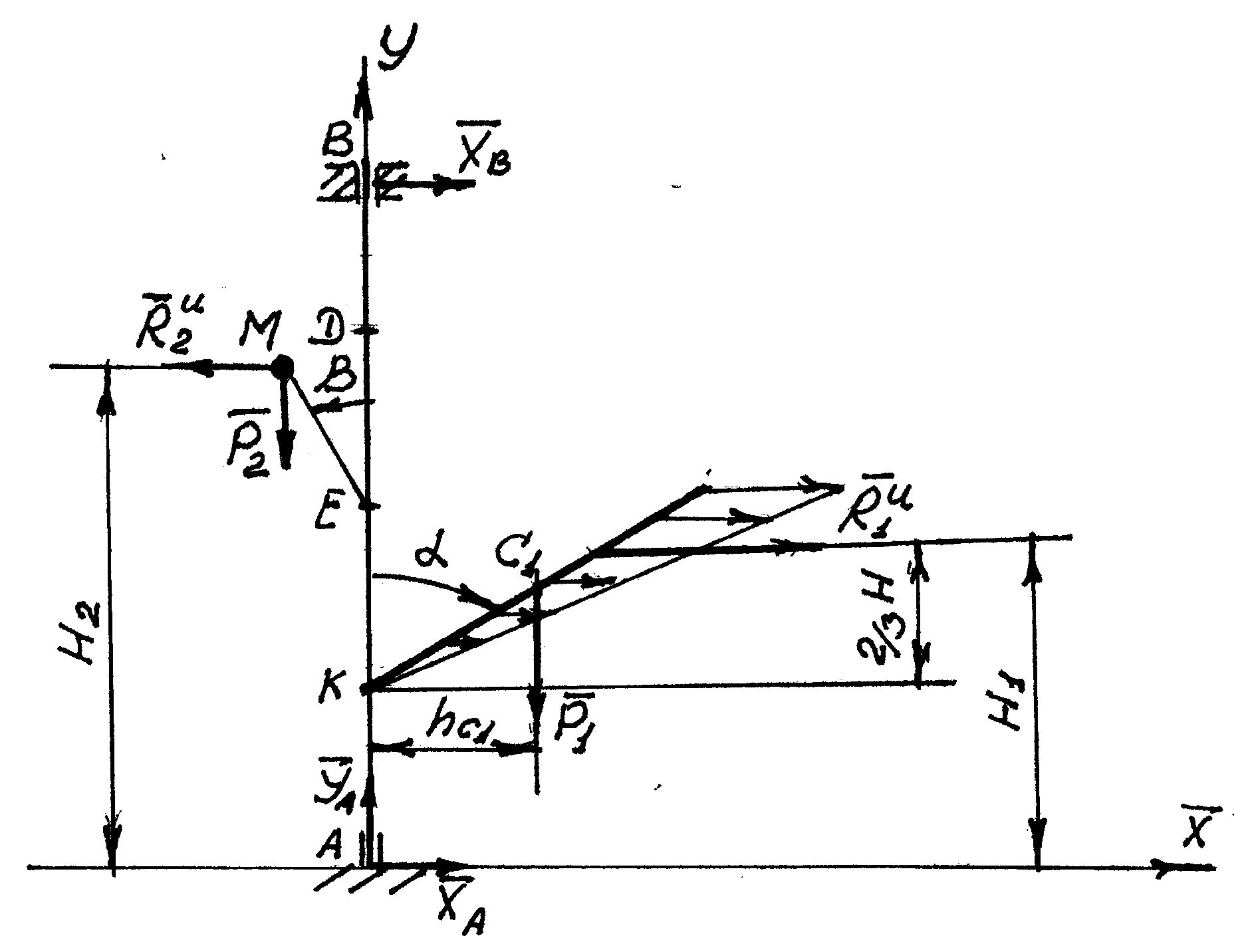
Рис. Д5

2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси АXУ так, чтобы стержни лежали в плоскости XУ и изобразим действующие на систему силы: активные силы - силы тяжести ₁ = m₁ , ₁= m₂ и реакции связей - составляющие реакции подпятника _А, _А и реакцию цилиндрического подшипника _В .

Согласно принципу Даламбера присоединим к этим силам силы инерции элементов однородного стержня и груза, считая его материальной точкой.

Так как вал вращается с постоянной угловой скоростью, то элементы стержня имеют только нормальные ускорения _nk, направленные к оси вращения и численно = ²h_k, где h_k - расстояния элементов от оси вращения. Тогда силы инерции будут направлены от оси вращения и численно = m_k , где m _k - масса элемента. Так как все пропорциональны h_k ,то эпюры параллельных сил инерции стержня 1 образуют треугольник.

Заменим полученную для стержня систему параллельных сил ее равнодействующей, равной главному вектору этих сил, то есть = , здесь m₁ - масса стержня 1, - ускорение его центра масс.

Сила инерции груза, принимаемого за точечную массу М, должна быть направлена в сторону, противоположную ее ускорению и численно будет равна = . Ускорения центров масс стержня 1 и груза равны: = h_c1, = h_2, где - расстояния от центра масс стержня и от груза до оси вращения и равны h_с1 = sin , h₂ = sin ,

Тогда по модулю = m₁ sin , = m₂ sin ,

Линия действия равнодействующей пройдет через центр тяжести соответствующей эпюры сил инерции, то есть на расстояние H от вершины треугольника К, где H = 2 cos  .

3. Согласно принципу Даламбера приложенные внешние силы (активные реакции связей) и силы инерции образуют уравновешенную систему сил.

Все эти силы лежат в одной плоскости, поэтому можно составить три уравнения равновесия:

_кх = 0; Х_А + Х_В +  = 0;

_kx = 0; У_А  Р₁  Р₂ = 0;

_А( _k) = 0; Х_В 4a Р₁h_с1 + Р₂ h₂  H₁ + H₂ = 0,

где H_1, H₂ - плечи сил , относительно точки А, равные H₁ = а+ H,

H₂ = 2а + cos .

Полученная система трех уравнений равновесия включает в себя три неизвестные реакции X_А, X_В ,Y_А, значения которых можно найти, подставив соответствующие величины (см. выше) и решив эту систему уравнений.