Задача д3 Применение теоремы об изменении кинетического момента системы

Методические указания. Задача Д3 – на применение теоремы об изменении кинетического момента системы относительно оси.

Пример

Рис.Д3

Однородная пластина массы М в виде равностороннего треугольника со стороной а вращается вокруг вертикальной оси, проходящей через вершину О с угловой скоростью . В начальный момент времени от точки А в направлении к точке Д начинает двигаться груз массы m по закону , при этом одновременно к пластине прикладывается вращающий момент (t – время в сек.). Определить закон изменения угловой скорости пластины.

Решение. Применяем теорему об изменении кинетического момента системы относительно оси Z, выражаемую уравнением

, (1)

где K_Z – кинетический момент системы, состоящей из пластины и груза, относительно оси Z; – главный момент всех внешних сил, приложенных к системе, относительно той же оси Z.

К системе приложены следующие внешние силы: реакции подпятника X_L, Y_L, Z_L, реакции подшипника P – X_P и Y_P и активные силы: силы тяжести пластины , приложенная в точке С – центре тяжести пластины и сила тяжести груза mg, а также пара сил с моментом М_вр. Согласно рисунку направления вращения пластины и направления вращающего момента положительны.

Определим выражение для кинетического момента системы

, (2)

где – кинетический момент пластины относительно оси Z;

– кинетический момент груза (материальная точка) относительно оси Z.

, (3)

где – момент инерции пластины относительно оси Z, который найдём по теореме Гюйгенса-Штейнера

. (4)

В (4) – момент инерции относительно оси, проходящей через центр масс С пластины и равный

. (5)

Отрезок

. (6)

Подставляя (5) и (6) в (4), находим

. (7)

При определении кинетического момента точки Д учтём, что она совершает сложное движение, поэтому

, (8)

где – кинетический момент груза относительно оси Z, обусловленный переносным движением ( – переносная скорость);

– кинетический момент груза относительно оси Z, обусловленный относительным движением груза ( – относительная скорость)

, (9)

где – относительная скорость, т.е. скорость движения груза по отношению к пластине;

– плечо вектора , т.е. длина перпендикуляра опущенного из точки О на линию действия вектора .

Так как – равносторонний, то АЕ – биссектриса, медиана и высота одновременно, поэтому . Следовательно

. (10)

Кинетический момент груза, обусловленный переносным его движением, определяется аналогично

, (11)

где ;

.

Подставляя выражения для ω и h_е в (11), получим

. (12)

Подставляя в (12) выражение для S как функции времени, находим

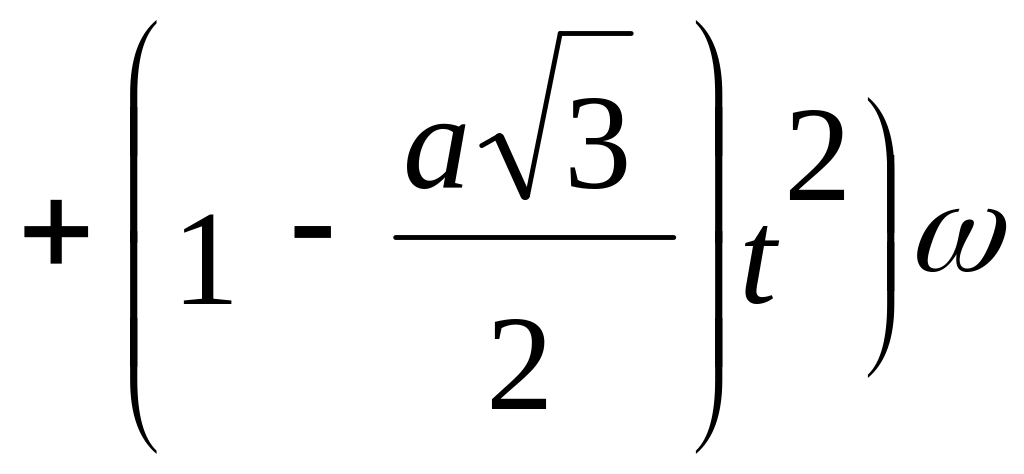. (13)

Знаки и положительны, т.к. оба вектора и сообщают движение грузу против хода числовой стрелки, если смотреть со стороны положительного направления оси Z.

Таким образом, подставляя найденные выражения для кинетических моментов пластины и груза в (2), получаем

. (14)