Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Самарская государственная академия путей сообщения
Кафедра механики
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Часть вторая
ДИНАМИКА
Методические указания
к выполнению расчетно-графических работ
по дисциплине «Теоретическая механика»
студентами дневной формы обучения
Составители: Ю.Д. Карышев
Л.В. Кудюров
В.Н. Новикова
В.М. Трухман
В.П.Червинский
Самара 2004
УДК 5311534
Динамика: Методические указания к выполнению расчетно-графических работ по дисциплине «Теоретическая механика» студентами дневной формы обучения. – Самара: СамГАПС, 2004 – 28с.
Утверждено на заседании кафедры «Механика» от 13.05.03 г., протокол № 8.
Печатается по решению редакционно-издательского совета СамГАПС.
Содержатся методические указания к выполнению расчетно-графических работ по дисциплине «Теоретическая механика» для студентов дневной формы обучения СамГАПСа.
Составители: Карышев Юрий Дмитриевич
Кудюров Лев Владимирович
Новикова Вера Николаевна
Трухман Вячеслав Михайлович
Червинский Вилен Петрович
Рецензенты: канд. техн. наук Н.Н. Лысач
канд. техн. наук Н.П. Красикова
Подписано в печать 29.12.04. Формат 60х84 1/16.
Бумага писчая. Печать оперативная. Усл. п.л. 1,75.
Тираж 200 экз. Заказ № 249.
Самарская государственная академия путей сообщения, 2002, 2004
1.Общие указания к выполнению Расчетно-графических работ
Расчетно-графические работы выполняются в соответствии с требованиями, изложенными в сборнике «Задания для выполнения расчетно-графических работ по теоретической механике студентами дневной формы обучения».
При выполнении расчетно-графических работ записи, чертежи, схемы должны быть выполнены в определенном масштабе, аккуратно. Условие задачи и величины, подлежащие определению, приводятся в краткой записи. Решение задач должно сопровождаться всеми необходимыми пояснениями и обосновываться ссылками на соответствующие теоремы или иные теоретические положения, на основе которых проводится решение.
На рисунках должны быть указаны направления векторов, которые определены в результате решения задачи.
Защита проводится в часы консультаций. Студент должен знать основы теории по теме работы, владеть методикой решения задач данного типа.
2. Динамика Задача д1 Динамика материальной точки
Методические указания. Решение задачи Д1 требует составления дифференциальных уравнений движения точки и их интегрирования при заданных начальных условиях (решение обратной задачи динамики). Решение задачи разбивается на два этапа. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения груза (точки) на участке АВ с учётом начальных условий, приведённых в таблице Д1 (см. Задания). Затем, зная время движения груза на участке АВ t1 или его длину l, определить скорость груза в точке В. После этого необходимо составить и проинтегрировать дифференциальные уравнения движения на участке ВС, приняв за начальные условия следующие: в момент прохождения груза через точку В t=0, V=Vв, х=0, у=0. При интегрировании уравнений движения на участке АВ в случае, если задана его длина, рационально перейти к интегрированию по переменной x, используя замену
.
Пример 1
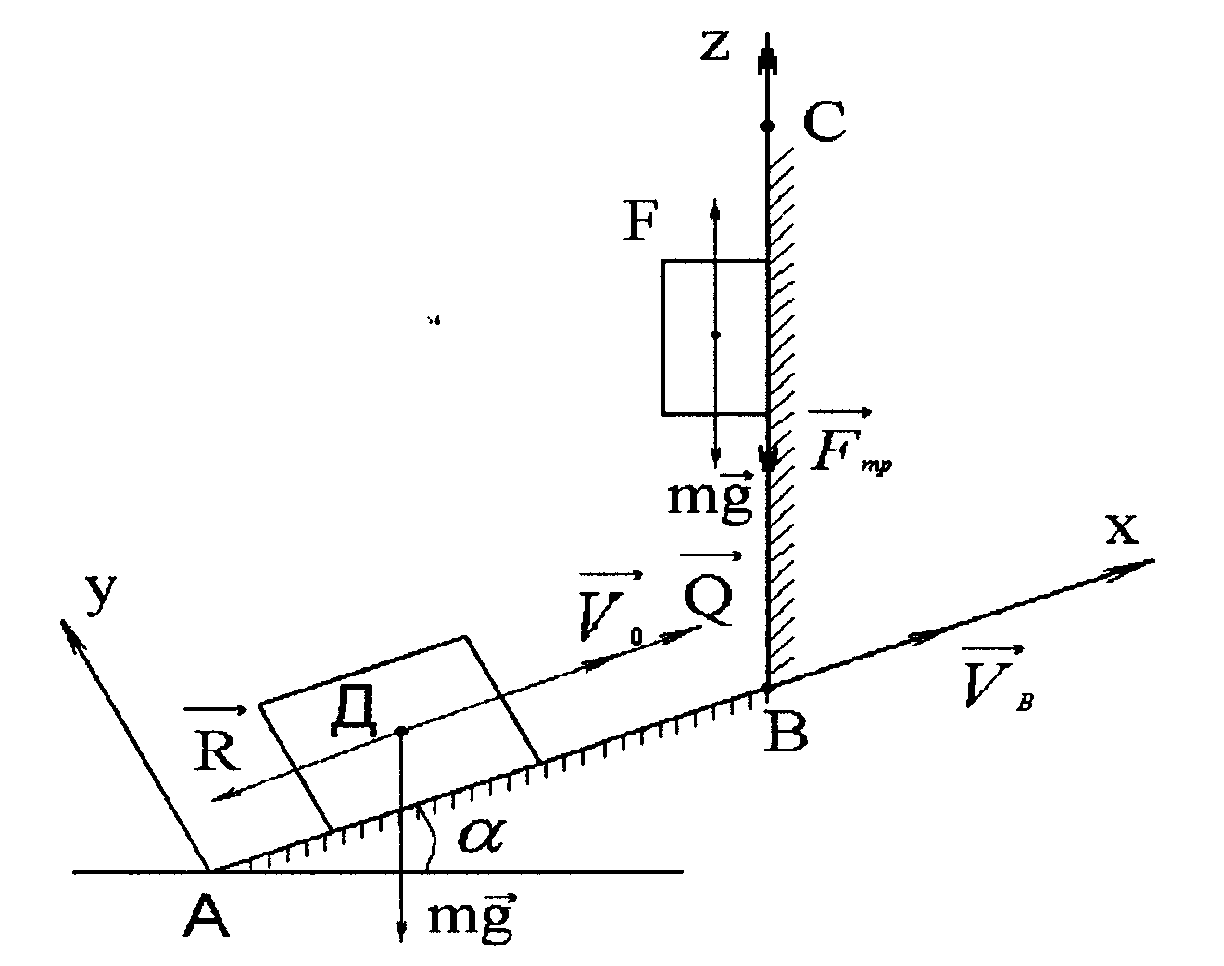
Рис. Д 1.1
Груз Д массы m, получив начальную скорость V0 в точке А, движется по траектории АВС. На участке АВ на груз действует сила тяжести, сила сопротивления R=kV2 и постоянная сила Q; длина участка АВ равна l. На вертикальном участке ВС на груз действует сила тяжести, постоянная сила трения Fтр и переменная сила F=at2, где t – время.
Определить закон движения груза на участке ВС –Z(t) .
Решение
1 Этап. На рисунке груз изображён в промежуточном положении и показаны все силы, действующие на него. Составляем дифференциальное уравнение движения груза в проекции на ось x
.
(1)
Замечание. В уравнении движения все переменные силы должны быть выражены через величины, от которых они зависят. Т.к. по условию задачи задана длина участка АВ, то в уравнении (1) перейдём от переменной t к переменной x, переписав его в виде
.
(2)
Разделяя переменные в уравнении (2), записываем
.
(3)
Беря интегралы от обеих частей равенства (3), получаем
или
. (4)
Константу С определим, используя начальные условия: при x = 0, V = V0, откуда
.
(5)
Подставляя (5) в (4), находим
.
(6)
Из (6) после преобразований окончательно получаем
.
(7)
Формула (7) даёт выражение для скорости как функции пройденного расстояния x. Подставляя вместо x величину l, получим значение скорости в точке В
.
(8)
Считаем, что в точке В скорость изменяет своё направление, не изменяя своей величины.
2
этап.
Рассматриваем движение груза на
вертикальном участке ВС. Найденная
скорость VB
будет на этом участке начальной, в точке
В z
= 0. На груз на участке ВС действует сила
тяжести, постоянная сила трения и
переменная сила
.
Уравнение движения груза в проекции на
ось Z
имеет вид
или,
обозначая
,
.
(9)
Умножая обе части равенства (9) на dt, получим
.
(10)
Интегрируя (9), находим
.
(11)
Используя начальное условие t = 0, V = VB определяем С1 = VB. Подставляя С1 = VB в (11), получаем
.
(12)
Учитывая,
что
,
уравнение (12) перепишем в виде
.
(13)
Интегрируя (13), найдём
.
(14)
Константу С2 определим по начальному условию: при t = 0, z = 0, откуда С2 = 0.
Таким образом, окончательно получаем закон движения груза на участке ВС
,
(15),
где Z – в метрах, t – в секундах.
Пример 2
Рис. Д1.2
Груз
Д массы m
движется по горизонтальному участку
АВ под действием постоянной силы
и силы сопротивления
.
Получив в точке В скорость
,
груз продолжает
движение в вертикальной плоскости под
действием только силы тяжести. Определить
закон движения груза в плоскости, т.е.
зависимости x
= x(t)
и y
= y(t),
а также угол между вектором скорости в
точке встречи С груза с прямой ВС.
Решение
1 Этап. Движение на участке АВ подробно рассмотрено в примере 1.
2 Этап. В результате анализа движения на участке АВ мы определили скорость в точке В1 по величине и направлению.
Составим дифференциальные уравнения движения в проекциях на оси x и y
;
(16)
.
(17)
Интегрируем уравнение (16)
.
(18)
С1
определим по начальному условию: при t
=0, Vx
=
VB.
Следовательно С1
=
VB.
Учитывая, что
,
запишем
.
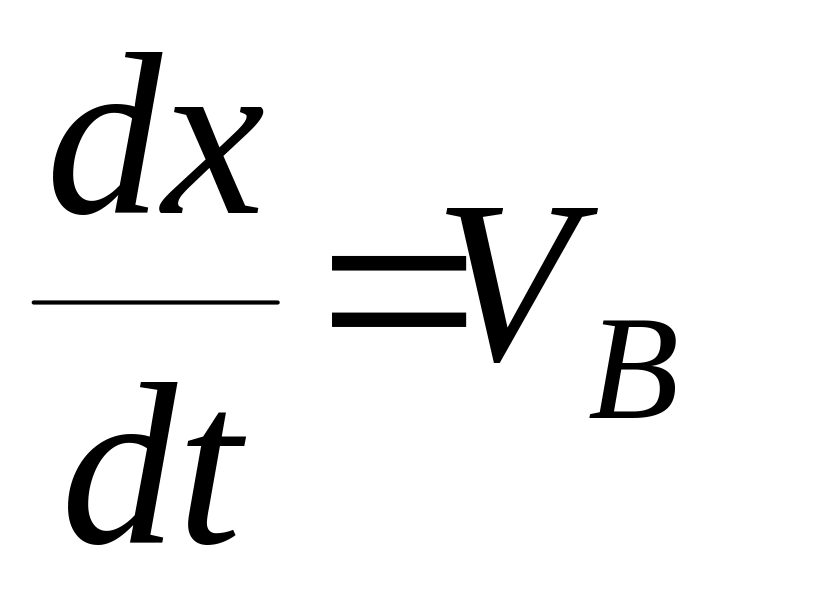(19)