Тест 2 - 12

Номер теста Вопрос	2	3	4	5	6
А1	1	2	1	3	4
А2	3	3	1	2	2
А3	3	1	3	4	3
А4	1	1	2	3	1
В1	Все числа, кроме -4 и0	-10		3	6
В2	При х=3 и х=-3	2/3		7,2
С1		4	Прямая у = х+3 с выколотой точкой (3,6)	При b=21	7

Номер теста Вопрос	7	8	9
А1	3	4	2
А2	1	2	1
А3	2	1	2
А4	3	1	1
А5			3
А6			4
В1	1	0	-(х+3)/2х
В2			х2/(х-5)
В3			(с+d)/(c-d)
В4
С1	При n=1, n=2	Все числа, кроме 3; ;	а=2; m=-10
С2			a=4; a≠-2

Номер теста Вопрос	10	11	12
А1	в	а	б
А2	г	в	г
А3	б	а	в
А4	г	в	б
А5	в	б	в
А6	б	г
А7	а	а
А8	в	в
В1	-1	2	1 или 5
В2		2	-1
В3	0,9	1
В4	-4	4	12
В5	-3	0,25

Ответы к задачам.

Понятие дроби.

1 .

2. Смотри ответы в учебнике.

3.

№1.10

1 способ: выполнить действия последовательно слева направо;

2 способ: Заметим, что разность множителей, расположенных в знаменателе, равна 3. Можно умножить каждое слагаемое на 3, а всю сумму на . Затем числители представить в виде 5-2, 8-5 и т.д., разделить каждое слагаемое числителя на знаменатель и , заметив некоторую закономерность, получить результат.

№1.11

а ) 22 = 21+1 б) а·а·…·а = а · 11…11

n - цифр n - цифр

Основное свойство дроби и его применение.

1 .

2. Смотри ответы в учебнике.

3.

4. Пример 1. Можно заметить, что знаменатель данной дроби представляет собой второй множитель в разложении по формуле двучлена а⁵ -1 , а числитель также представляет второй множитель в разложении двучлена (а²)⁵-1. Мы сможем упростить эту дробь, умножив числитель и знаменатель данной дроби на а²-1. Имеем:

Пример 2. Числитель и знаменатель данной дроби - однородные многочлены третьей степени (степень каждого члена многочлена равна 3). Поэтому, если числитель и знаменатель разделить на b³, то получим дробь, значение которой зависит от :

Из условия

3a+7b=2(3a-b), 3a+7b=6a-2b, 3a=9b,

Подставив это значение в преобразованную дробь, найдем

Пример 3. Для решения задачи попытаемся сократить данную дробь. Числитель очевидно раскладывается на множители : 3(x-2). Значит, если данная дробь сократима, то такой же множитель должен содержать и знаменатель дроби.

Попробуем представить знаменатель в виде произведения с помощью метода неопределенных коэффициентов:

x³-3x-2=(x-2)(x²+ax+1)= x³+a∙ x²+x-2∙ x²-2ax-2= x³+(a-2)∙ x²+(1-2a)x-2, получим систему , отсюда a=2.

Итак, x³-3x-2=(x-2)(x²+2x+1). Имеем:

Полученная дробь при всех x≠-1 принимает положительные значения. Учитывая, что при x=2 исходная дробь не имеет смысла, делаем вывод, что данная дробь положительна при всех х, кроме -1 и 2.

Пример 4. Для ответа на вопрос задачи было бы удобно выделить

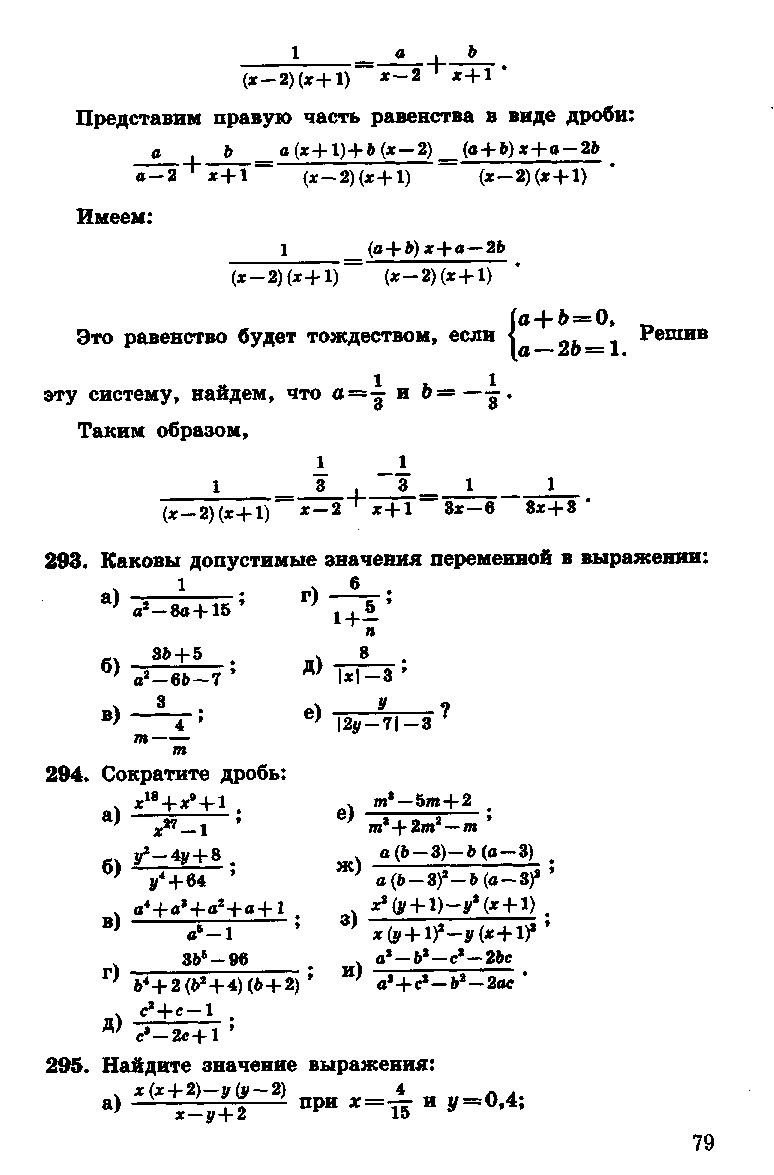
Пример 6.

5. 6. Указание. Умножить и разделить левую часть равенства на 1-х.

7. 8. При 9. 2 +

10. Указание. Допустить противное, что дробь сократима.

Умножение и деление дробей.

1 .

2. Смотри ответы в учебнике.

3.

Сложение и вычитание алгебраических дробей.

1 .

2. Смотри ответы в учебнике.

3. № 2.67. Выполнить сложение последовательно слева направо.

№ 2.78

а) Воспользоваться тождеством

б) Воспользоваться тождеством

4. 5. Указание. Умножить числитель и знаменатель второй дроби на 4, а третьей и четвертой дробей на 2. После этого выполнить все действия с дробями.

6. Указание. Каждая дробь этой суммы имеет вид , причем разность m-n постоянна и равна а=4, значит n+a=m.

Воспользоваться тождеством

7. Указание. Представьте левую часть равенства в виде

Возведение дроби в степень.

1. Смотри ответы в учебнике.

Все действия с дробями.

1 .

2. Смотри ответы в учебнике.

3. Выполнить действия.

4. Указание. Выражение тождественно равно . Оно не зависит от и, причем значения выражения a,a+b, a-5b при дробных а и целых b отличны от нуля.

5. а) -1; б) у²-4; в) и г) Указание. Вынести за скобки и затем преобразовать: в) ; г)