Итоговая отметка в рамках этого зачета равна среднеарифметическому значению набранных Вами баллов.

О н [Гена] очень любил читать точные и серьёзные книги: справочники, учебники или расписания движения поездов.

Успенский Э.Н.

Крокодил Гена и его друзья.

2. Теоретические сведения

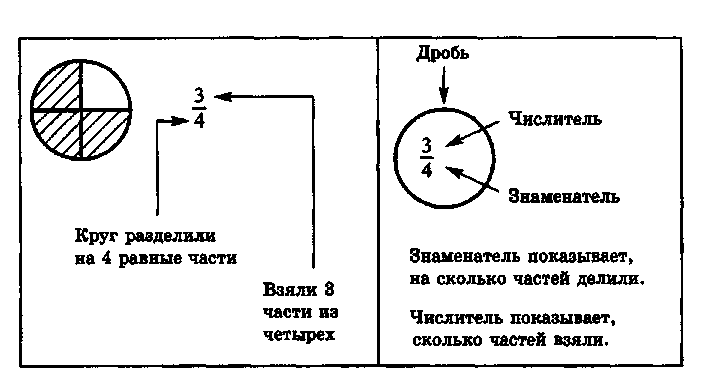
Обыкновенной дробью называется число вида

где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.

Если n = 1, то дробь имеет вид и её часто записывают просто m. Отсюда, в частности, следует, что

любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.

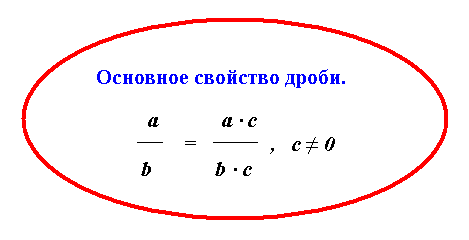
Основное свойство дроби.

Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.

Несократимая дробь, арифметическая дробь, числитель и знаменатель которой являются взаимно простыми числами (т. е. не имеют общих делителей); например, .

Всякую дробь можно представить в виде несократимой дроби, разделив числитель и знаменатель на их наибольший общий делитель.

Целые числа - натуральные числа, противоположные им отрицательные числа и число 0.

Множество всех целых чисел принято обозначать знаком Z.

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью ,

где числитель m — целое число, а знаменатель n — натуральное число.

Алгебраическая дробь – это выражение вида , где A и B могут быть числом, одночленом, многочленом.

Как и в арифметике, A называется числителем, B – знаменателем. Арифметическая дробь является частным случаем алгебраической.

Натуральные числа (естественные числа) — числа, которые используются при счёте (как в смысле перечисления, так и в смысле исчисления).

Множество всех натуральных чисел принято обозначать знаком N.

Существует бесконечное множество натуральных чисел — для любого натурального числа найдётся другое натуральное число, большее его.

Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения, и при этом не содержит никаких других действий с этими числами и переменными.

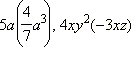
Стандартный вид одночлена. Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена, сумму показателей степени переменных называют степенью одночлена.

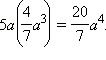
Многочленом называется сумма одночленов.

Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида. Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.

Наибольшим общим делителем (НОД) одночленов, называют общий делитель двух одночленов, име­ющий по каждой из переменных наивысшую возможную степень.

Чтобы найти НОД двух одночленов, нужно взять переменные, входящие в каждый из них, затем из показателей, с которыми они входят в эти одночлены, выбрать наименьшие (или любой из них, если эти показатели равны друг другу) и перемножить полученные степени.

Коэффициенты не учитываются

Наименьшим общим кратным (НОК) двух одночленов называется их общее кратное, имеющее по каждой из переменных наименьшую из возможных степеней.

Коэффициенты не учитываются

Чтобы получить НОК двух одночленов, нужно взять все перемен­ные, входящие хотя бы в один из них, а из показателей, с которы­ми они входят в эти одночлены, выбрать наибольшие, после чего перемножить полученные степени. Если переменная входит лишь в один одночлен, то ее берут с тем показателем, с которым она в не­го входит.

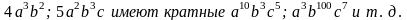
Алгоритм сокращения дроби:

1.Разложить на множители числитель и знаменатель дроби, если это необходимо.

2.Разделить числитель и знаменатель дроби на ненулевой многочлен.

3.Записать полученную дробь.

Алгоритм сложения и вычитания дробей с разными знаменателями.

Чтобы сложить или вычесть дроби с разными знаменателями, надо:

Привести данные дроби к наименьшему общему знаменателю.

Сложить или вычесть полученные дроби.

План действий:

1. Раскладываем все знаменатели на множители.

2. Из первого знаменателя выписываем произведение всех его множителей, из остальных знаменателей приписать к этому произведению недостающие множители. Полученное произведение и будет общим (новым) знаменателем.

3. Найдём дополнительные множители для каждой из дробей: это будут произведения тех множителей, которые имеются в новом знаменателе, но которых нет в старом знаменателе.

4. Найдём для каждой дроби новый числитель: это будет произведение старого числителя и дополнительного множителя.

5. Запишем каждую дробь с новым числителем и общим (новым) знаменателем.

Алгоритм умножения дробей:

1. Разложить числитель и знаменатель каждой дроби на множители, если это возможно.

2. Умножить числитель на числитель, знаменатель на знаменатель.

3. Выполнить сокращение полученной дроби, если это возможно.

Произведение двух дробей равно дроби, числитель которой равен произведению числителей этих дробей, а знаменатель – произведению знаменателей.

то

Дроби 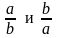называют обратными друг другу.

Их произведение равно 1.

Чтобы разделить дробь на дробь, надо умножить первую дробь на дробь, обратную второй.

При возведении дроби в степень надо:

1) Возвести в эту степень числитель и знаменатель

2) Разделить степень числителя на степень знаменателя

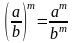
Алгебраическое выражение. Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок составляют алгебраические выражения.

Числа также называют алгебраическими выражениями.

Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением:

Если кроме указанных действий входит действие деления на выражение, содержащее переменные, то выражение называют дробно-рациональным:

Целые рациональные и дробно-рациональные выражения вместе называются рациональными.

Если входит еще и действие извлечения корня, то такое выражение называют иррациональным.

Значения переменных, при которых алгебраическое выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называют областью определения алгебраического выражения или областью допустимых значений (кратко ОДЗ).

Дробные выражения не имеют смысла при тех значениях переменных, которые обращают знаменатель в нуль.

Целое выражение имеет смысл при любых значениях входящих в него переменных.

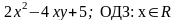
Если соответственные значения двух выражений, содержащих одни и те же переменные, совпадают при всех допустимых значениях переменных, то выражения называют тождественно равными.

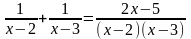тождественно равны

тождественно не равны

Тождеством называют равенство, верное при всех допустимых значениях входящих в него переменных.

Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.

Ответ: х = 5

Ответ: х = {4;5}

Где отсутствует точное знание, там действуют догадки, а из десяти догадок девять - ошибки.

Г орький М.

О том, как я учился.

3. Тест для самопроверки.

Тест 1

1

2

3

4

5

6

7

8

9

10

Тест 5 . Сложение и вычитание дробей с разными знаменателями.

Тест 4. Сложение и вычитание дробей с одинаковыми знаменателями.

Тест 6. Умножение дробей. Возведение дроби в степень.

Тест 7 . Деление дробей.

Тест 9. Итоговый. «Рациональные выражения и их преобразования»

Тест 10. Алгебраические дроби - 1.

Тест 11. Алгебраические дроби - 2.

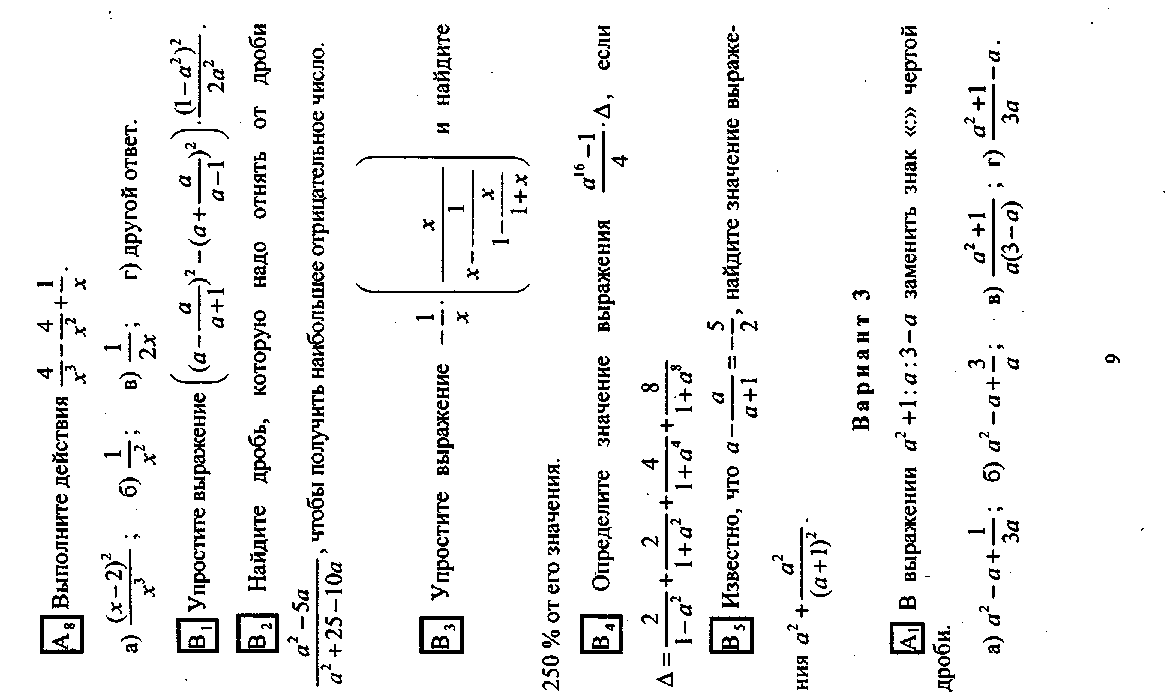
Тест 12. Алгебраические дроби - 3.

Зачет №2 «Тест для самопроверки»

Критерии оценивания

В рамках этого зачета Вам выставляется отметка за каждый Ваш ответ из числа предложенных вопросов теста для самопроверки.

Критерии отметки за ответ по выбору:

• 5 баллов - за правильный ответ;

• 0 баллов - за неправильный ответ.

Критерии отметки за ответ на задание с развернутым ответом из теста:

5 баллов - Приведена верная последовательность шагов решения и получен верный ответ;

• 4 балла - за верный, но не лаконичный («растянутый») или стилистически неверно выстроенный ответ;

• 3 балла - за ответ, по которому можно судить, что Вы понимаете суть, но упускаете существенные нюансы (не полный по смыслу ответ);

• 0 баллов - за отсутствие или неверный ответ.

Итоговая отметка в рамках этого зачета равна среднеарифметическому значению набранных Вами баллов.

Приведена верная последовательность шагов решения: