7

ЛАБОРАТОРНАЯ РАБОТА №1

Изучение дифракционной решетки с помощью гониометра

Цель работы: ознакомление с отражательной дифракционной решеткой, применение ее для определения длин волн линий спектра источника света, а также определение характеристик решетки.

1. Принадлежности: гониометр, отражательная дифракцион­ная решетка, плоскопараллельная стеклянная пластинка, ртутная лампа, лампа накаливания.

2. Теория дифракционной решетки.

Дифракционная решетка представляет собой стеклянную или металлическую пластинку, на которой с помощью делительной ма­шины через строго одинаковые интервалы нанесены параллельные штрихи. Для получения двух или более одинаковых решеток изго­тавливают из специальной пластмассы реплики гравированных ре­шеток. Решетки могут быть отражательные или прозрачные, плоские или вогнутые. Чтобы разобраться с физическими основами работы дифракционных решеток, следует рассмотреть дифракцию Фраунгофера на N щелях (т.е. случай амплитудной, плоской диф­ракционной решетки).

2.1. Дифракция Фраунгофера на N щелях (амплитудная дифракционная решетка)

Пусть на систему из N строго периодических щелей (период ) падает плоская монохроматическая волна под углом к плос­кости решетки (см. рис. 8.1 а).

Для определения зависимости интенсивности от угла дифракции мы проведем процедуру, аналогичную соотношениям 7.1 7.4 с той лишь разницей, что у нас вместо двух щелей имеется N щелей. Итак, от элемента n-ой щели, который расположен на расстоянии от ее начала, возбуждается волна:

(8.1)

Вся n-я щель пошлет в направлении угла волну:

. (8.2)

Интерференция волн от всех N щелей приводит к следующему:

. (8.3)

Введем следующие обозначения:

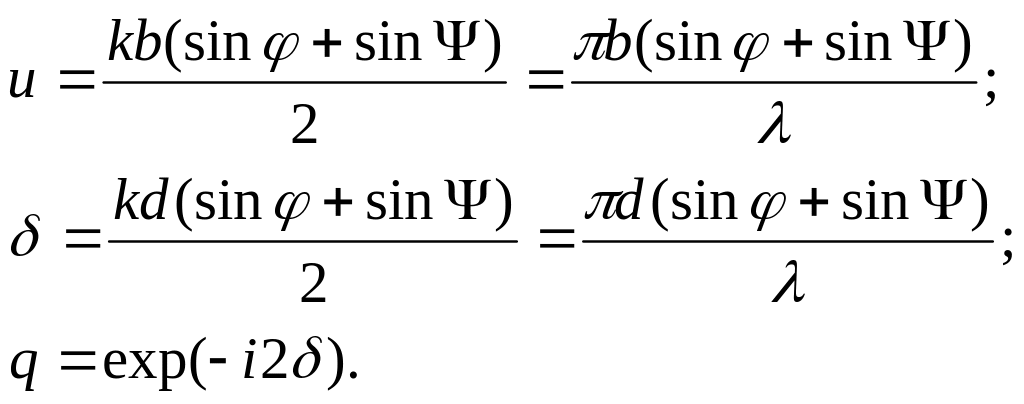
Тогда для (8.3) запишем:

(8.4)

Искомую интенсивность определим:

(8.5)

В полученном выражении (8.5) функция отражает диф­ракцию Фраунгофера на щели шириной b. График этой функции представлен на рисунке 8.2а. Зависимость (при N=5) представлена на рисунке 8.2б. Анализ функций и показыва­ет, что максимумы этих функций определяются соотношениями:

, и т.д. (8.6)

, где и т.д. (8.7)

Минимумы этих функций удовлетворяют следующим соотношени­ям:

, где и т.д. (8.8)

, где . (8.9)

Анализ функции (8.5) показывает, что наибольшее количест­во энергии светового пучка, падающего на амплитудную дифракци­онную решетку, дифрагирует в направлении нулевого максимума ("белого") максимума. Это обстоятельство ведет к возникновению сложностей при создании светосильных спектральных приборов с использованием амплитудной дифракционной решетки. По этой при­чине на практике используется, как правило, профиллирован­ные (фазовые) дифракционные решетки (см., например, рисунок 8.1б). В такой решетке при отражении от каждого штриха внесена дополнительная разность хода (см. рис. 8.1б), которая приводит к изменению порядка, соответствующего зеркальному отражению. При условии зеркальное отражение соответству­ет второму порядку, что приводит к распределению интенсивности, представленному на рис. 8.2 в. Решетка, как говорят, "концентрирует" энергию в данный (в нашем случае второй) по­рядок. Угол между нормалями к поверхности решетки и к от­ражающей грани штриха называют углом блеска решетки (см. рис. 8.1 б).