Дополнительные задания

• Вводится действительное число X. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить: 2x⁴-3x³+4x²-5x+6. Разрешается использовать не более четырех умножений и четырех сложений и вычитаний.

• Вводится действительное число X. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить: 1-2x+3x²-4x³ и 1+2x+3x²+4x³.

• Поменять местами значения двух целых переменных A и B, не используя дополнительных переменных.

• Вводится действительное число A. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить: а) A⁶ за три операции умножения. б) A⁷ за четыре операции умножения. в)A⁸ за три операции умножения. г) A⁹ за четыре операции умножения. д) A¹⁰ за четыре операции умножения.

4. Условный оператор Лабораторная работа 7.(учим компьютер спрашивать)

1. Вводятся три целых числа. Определить, могут ли они являться сторонами треугольника.

2. Вводятся два целых числа. Поместить большее из них в переменную MAX, а меньшее в переменную MIN. Если числа равны, то выдать об этом сообщение.

3. Вводятся два целых числа. Определить, одинаковая ли у них четность.

4. Вводятся координаты точки на плоскости (X,Y). Определить, в какой четверти находится эта точка.

5. Вводятся три целых числа. Найти из них максимальное значение.

6. Вводятся коэффициенты A,B и C квадратного уравнения Ax²+Bx+C=0. Определить количество действительных корней этого уравнения.

7. Заданы два прямоугольника размерами A*B и C*D. Определить, можно ли поместить второй прямоугольник в первый при условии параллельности и перпендикулярности их сторон.

8. Вычислить функцию:

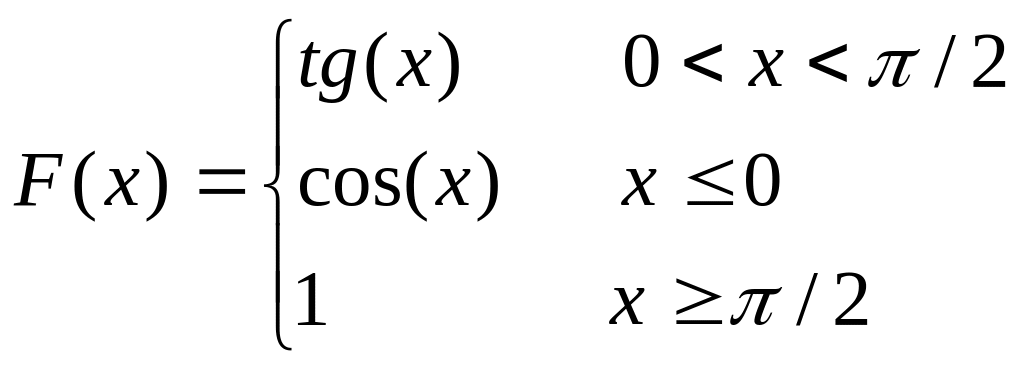
9. Поля шахматной доски пронумерованы слева направо и сверху вниз числами от единицы до восьми. Заданы два поля. Определить, являются ли они по­лями одного цвета.

10. Поля шахматной доски пронумерованы слева направо и сверху вниз числами от единицы до восьми. Заданы два поля. Определить, угрожает ли ладья, стоя­щая на первом поле фигуре, стоящей на втором поле.

11. Заданы размеры плоского прямоугольного отверстия (a*b) и размеры трехмерного кирпича (c*d*e). Определить, можно ли протащить кирпич через отвер­стие, соблюдая параллельность и перпендикулярность сторон.

12. Вводится номер года. Определить, является ли этот год високосным (год високосный, если его номер кратен четырем, однако из кратных ста високосными являются лишь кратные четыремстам; например, 1700, 1900 – не високосные годы, а 2000 - високосный).

13. Вводятся коэффициенты (k1,b1,k2,b2), определяющие две прямые y=k1*x+b1 и y=k2*x+b2. Найти точку пересечения этих прямых или указать, что они совпа­дают или параллельны.

14. Даны стороны и диагонали параллелограмма. Определить, является он ром­бом, прямоугольником или квадратом.

15. Вводятся координаты трех точек. Проверить, лежат ли все три точки на одной прямой.

16. Даны действительные числа x, y (xy). Меньшее из этих чисел заменить их полусуммой, а большее – их удвоенным произведением.

17. Вводится действительное число. Выделить его целую и дробную части, преоб­разовав их в целые числа; сообщить, если дробная часть равна нулю.

18. Имеется стол прямоугольной формы размером a*b (a и b – целые числа, a>b). В каком случае на столе можно разместить большее ко­личество картонных прямоугольников с размерами c*d (c и d – целые числа, c>d): при размещении их длинной стороной вдоль длинной стороны стола или вдоль короткой. Пря­моугольники не должны ле­жать один на другом и не должны свисать со стола.

19. Вводятся две скорости: одна в километрах в час, а другая в метрах в секунду. Определить, какая из скоростей больше.

20. Известны площади круга и квадрата. Выяснить, уместится ли круг в квадрате.

21. Известны площади круга и квадрата. Выяснить, уместится ли квадрат в круге.

22. Даны объемы и массы двух тел. Определить, у какого тела больше плотность материала.