I I частина ( 4 бала).

Розв’язання завдань 6-7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6. Знайдіть кут між бісектрисою та продовженням однієї із сторін даного кута, який дорівнює 90°.

7. З однієї точки А проведено дві дотичні до кола. Доведіть, що відрізки до­тичних АВ і АС рівні, якщо В і С – точки дотику.

I I I частина (3 бала).

Розв’язання завдання 8повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. Дано: МО = NO, РМО = КNО.

Доведіть: РNМ= КМN.

Варіант № 5.

I частина (5 балів)

Завдання 1-5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1. Якщо на малюнку ВD=12см, СD=9см, то ВС дорівнює:

А) 21см; Б) 3см; В) 6см; Г) 2см.

2. а||в, 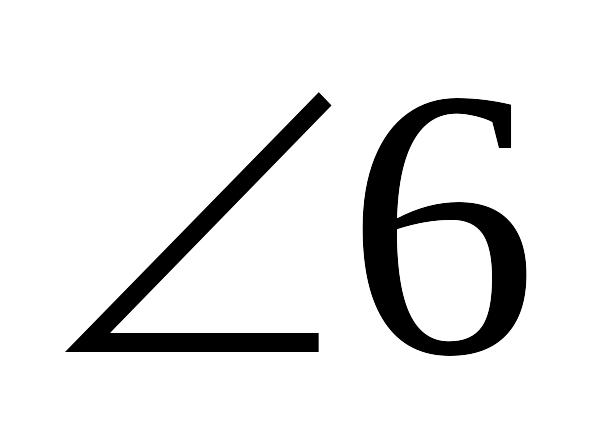=54˚, с - січна. Знайдіть 4 та 2.

А) 54˚та 54˚ ;

Б) 54˚та 36˚ ;

В) 126˚та 126˚ ;

Г) 54˚та 126˚ .

3. У рівнобедреному трикутнику АВС АВ = 7 см, ВС = 5 см. Знайдіть периметр ∆ABC, якщо його основою є сторона AB.

А) 12 см; Б) 17 см; В) 19 см; Г) 20 см.

4. Трикутники BCD і AFE рівні. Знайдіть сторону AE, якщо ВС = 7 см, EF=14 см, P_∆BCD = 29 см.

А) 29 см; Б) 13 см; В) 8 см; Г) 4 см.

5. Кола, радіуси яких 3 см і 2 см, мають внутрішній дотик. Знайдіть відстань між їх центрами.

А) 10 см; Б) 8 см; В) 5 см; Г) 1 см.

I I частина ( 4 бала).

Розв’язання завдань 6-7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6. Знайдіть кут між бісектрисою та продовженням однієї із сторін даного кута, який дорівнює 72°.

7. З однієї точки М проведено дві дотичні до кола. Доведіть, що відрізки до­тичних МР и MQ рівні, якщо Р і Q – точки дотику.

I I I частина (3 бала).

Розв’язання завдання 8повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

8. По один бік від прямої АВ позначено точки Q і D так, що QAD = DBQ і DAB = QBA. Доведіть, що AQ = BD і AD = BQ.

Варіант № 6.

I частина (5 балів)

Завдання 1-5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

1. Знайдіть кут між бісектрисою та стороною кута, який дорівнює 50˚.

А) 130˚; Б) 75˚; В) 25˚; Г) 100˚.

2. а||в, с - січна, 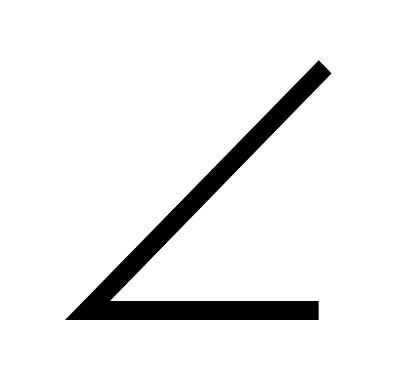_{3 =20}˚. Знайдіть 5- 6.

А) 20˚;

Б) 140˚;

В) 0˚;

Г) 160˚.

3. У рівнобедреному трикутнику MNF MF = 10 см, MN = 8 см. Знайдіть периметр ∆MNF, якщо бічними сторонами є сторони MN і NF.

А) 18 см; Б) 26 см; В) 28 см; Г) 30 см.

4. У рівнобедреному трикутнику АВС відрізок ВD – медіана, АС – основа. Знайдіть Р_DАВС, якщо Р_DАВD=12см, ВD=4см.

А) 24 см; Б) 16 см; В) 20 см; Г) інша відповідь.

5. Знайдіть довжину кола, якщо площа круга 36π.

А) 12π; Б) 6π; В) 3π; Г) 24π.