34 Точки Npt, tpN событий развития нематоды

У всех этих 34 временных координат t^p_N , простых чисел, их порядковые номера – последовательны. Т.е. равны 47, 48, 49, 50,….,78, 79, 80, или меняются по закону: к к+1. Эти номера явно указаны в выше расположенной таблице, а также в сводной таблице № 1 всех 137 последовательных простых чисел (стр.42)

3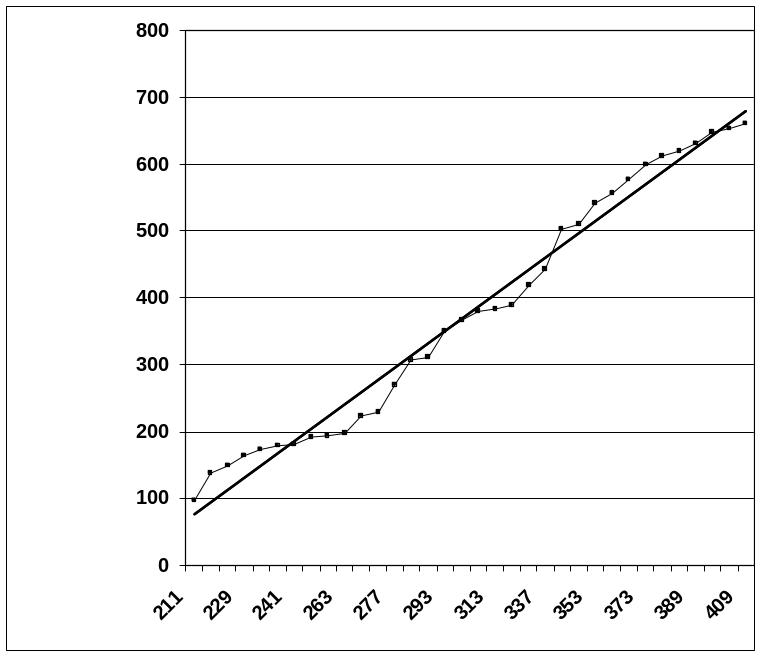

Здесь по горизонтальеой оси – время в минутах а по вертикальной-номера событий во времени.

Рис. 2а, см. ниже -34-ка.- область ускоренного развития нематоды полиномиального типа с двумя внутренними (A, B) и внешними (C, D) касательными (все номера простых времен – последовательны: k k+1, k = (13¹ – 46³⁴ )). Точка - точная середина 57-ки и правый край 17-ки из 34-ки, а также точка пересечения внутренних касательных А₁ и В₂. Коэффициенты корреляции точек 4-х ка-сательных:А: r =0,99997694; B: r =0,999 999 99 ;C: r =0,999 99 43

D : r = 0,999 892 78, (r- по 3-4 точкам).См. Рис.( 2а) ниже).

Рис. 2_а

ОПИСАНИЕ КАСАТЕЛЬНЫХ РИС.2а -

А₁, В₂ -ПЕРВАЯ И ВТОРАЯ ВНУТРЕННИЕ,

С_л, D_п – ЛЕВАЯ И ПРАВАЯ ВНЕШНИЕ КАСАТЕЛЬНЫЕ

А ₁ : 1-ая внутренняя.

(р, р) (р, опыт)

197, 263 I263, 3

229, 271 I271, 5 Y = aX + b Рис.2а

346, 56;302, 14 * Без точки пересечения (*): 541, 353 I354,0 r_(р-р)=0,999 992 38

а = 3,81515314, в = - 805,680 27; =295,67; = 322,33----

r_{(р-опыт)}=0,999 996 94

а = 3,788 296 4, в = - 800, 012 61; =296,27; = 322,33---

С точкой пересечения

r_(р-р)=0,999 991 29

а = 3, 814 696 14, в = - 805,661 94 =297,285; = 328,39---

r_{(р-опыт)}=0,999 976 9

а = 3, 700 175 3, в = - 800,0 30 87 =297,735; = 328,39---

В ₂ : 2-ая внутренняя.

(р, р) (р, опыт)

163, 229 I229, 5

173, 233 I233, 3 Y = aX + b Рис.2а

346, 56;302, 14 * Без точки пересечения : 419, 331 I331,1 r_(р-р)=0,999 999 99

а = 2,50998801, в = - 411,806 83; =264,33; = 251,67----

r_{(р-опыт)}=0,999 998 88

а = 2,517 676 75, в = - 800, 012 61; =264,633; = 251,67---

С точкой пересечения

r_(р-р)=0,999 999 99

а = 2, 509 98454 , в = - 411,80611 =273,785; = 275,39---

r_{(р-опыт)}=0,999 997 61

а = 2, 519 373 08, в = - 414,943 41 =274,01; = 275,39---

С_л : левая внешняя. Y = aX + b

(р, р) (р, опыт) r_(р-р)=0,999 986 62

163, 229 I229, 5 а = 3,056 928 03, в = - 538, 132 11;

173, 233 I233, 3 =271,67; = 292,33----

541, 353 I354,0

r_{(р-опыт)}=0,999 993 43

а = 3,042 118 55, в = - 535, 934 14; =272,27; = 292,33

D_п : правая внешняя. Y = aX + b

(р, р) (р, опыт) r_(р-р)=0,999 892 78

197, 263 I263, 3 а = 3,176 242 81, в = - 636, 257 18

419, 331 I331,1 =334,33; = 425, 67----

661, 409 I410,0

r_{(р-опыт)}=0,999 823 72

а = 3,160 324 94, в = - 632, 41012; = 334,8; = 425, 67---

* * *