784 : , Которая

=136,9765653.., (14)

где _o 

Итак,

(15) »

(-конец кавычек !) т.е., получившееся относительное отличие равно не более 0,0434 % Отметим, что отличие дроби (14) от 33-го простого числа, от 137, еще меньше : 0,0217%.

Таким образом, указанные данные позволили нам сделать вывод, что 33-е простое число 137 как номер последнего простого -773-ей минуты - перед последним делением на 784 минуте, приводит в определённом смысле к значению длительности эмбрионального развития гермафродита нематоды. Этот вывод позволил нам проэстраполировать локальное значение ВАЖНОСТЬ(!) одного простого числа на все малые –до 137-го –р-числа.

В заключение отметим, что «элементарное» «деление» (14) было реализовано спустя несколько месяцев после определения кванта времени , при этом «попутно» было найдено .Т.е. из чисто биологических данных найдена комбинация из c,h,e(!!!)-трех мировых постоянных (-замечание А). Этим примером, несколько оправдываясь, мы подтверждаем «доказательную» ценность «хронологии» этапов исследования.

* * *

А. Р-редукция:[784х784] [57х57]^р

И

Р-Р-аксиоматика, принцип Пигмалиона,

сигнатура

Двумерие натурального ряда и симметрии

интенсивного этапа развития

(на примере нематоды)

А ЗАЧЕМ

ИСПОЛЬЗОВАТЬ Р-ЧИСЛА ?

На страницах 27 – 34 этого выпуска мы начали обсуждение выше сформулированного вопроса об алгорит-мической и (или) информативной относительной ценности

простых (-ПЕРВИЧНЫХ –по польски, русская транскрип-ция, В. Серпинский) и составных чисел. Эти последние при учете возможной разной размерности сомножителей -часть из них может её не иметь (!)-могут быть «сделаны» некоммутативными. Подчеркнем тривиальный факт, что составные числа «сделаны» из ПЕРВИЧНЫХ или ПРОСТЫХ чисел-сомножителей.

Отметим, что все самые основные величины современной теоретической физики представляют собой или собственные значения, (и) или собственные функции определённых операторов, имеющих важные свойства симметрии. Причем, собственные функции в основном являются известными, уже изученными - хотя бы численно-спецфункциями.

Простые Р-числа – хотя и не полностью изучены ( если

говорить о всех уже «табулированных» нескольких десятках миллионах Р-чисел вместе с их порядковыми номерами) – достаточно известны, удобны в обращении и приведены в школьных справочниках в необходимых нам объёмах – немного меньше тысячи чисел. В итоге, чего мы хотим ? – декомпактифицировать-ни мало ни много(!)-небольшой отрезок натурального ряда (N-ряда) и выяснить роль Р-чисел - не всех, а подчиняющихся π-принципу – в фиксации определённых двумерных симметрий N-ряда и, особенно, симметрий Р-Р-пар (см.Табл.№2 и стр. 46). упомянутый выше π-принцип хотя бы при частичной предварительной алгоритмизации и использовании опытных данных в максимальном объёме сводится к удалению определённой доли Р-чисел (см. стр. 51 ).

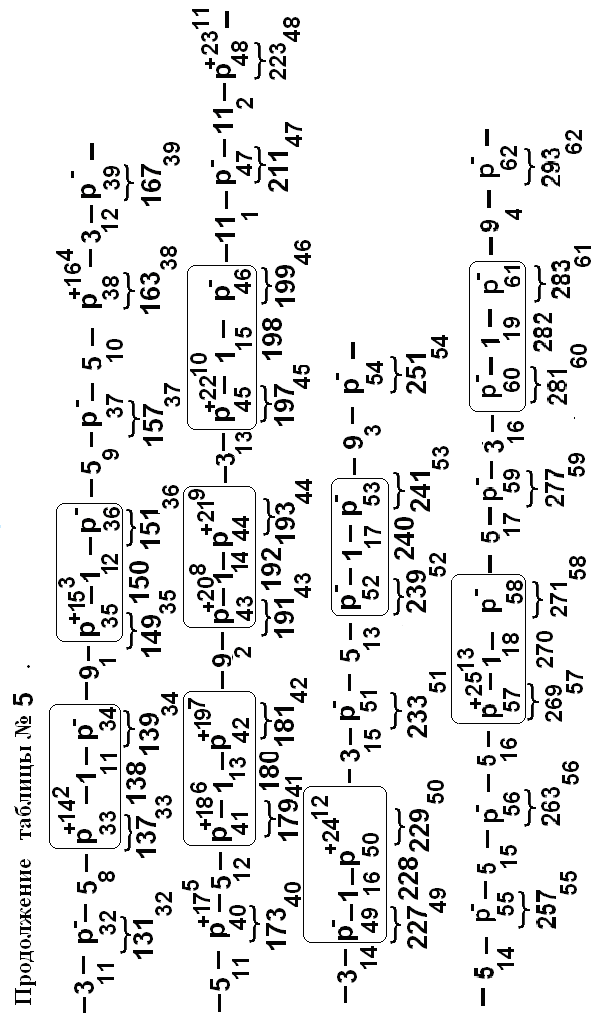
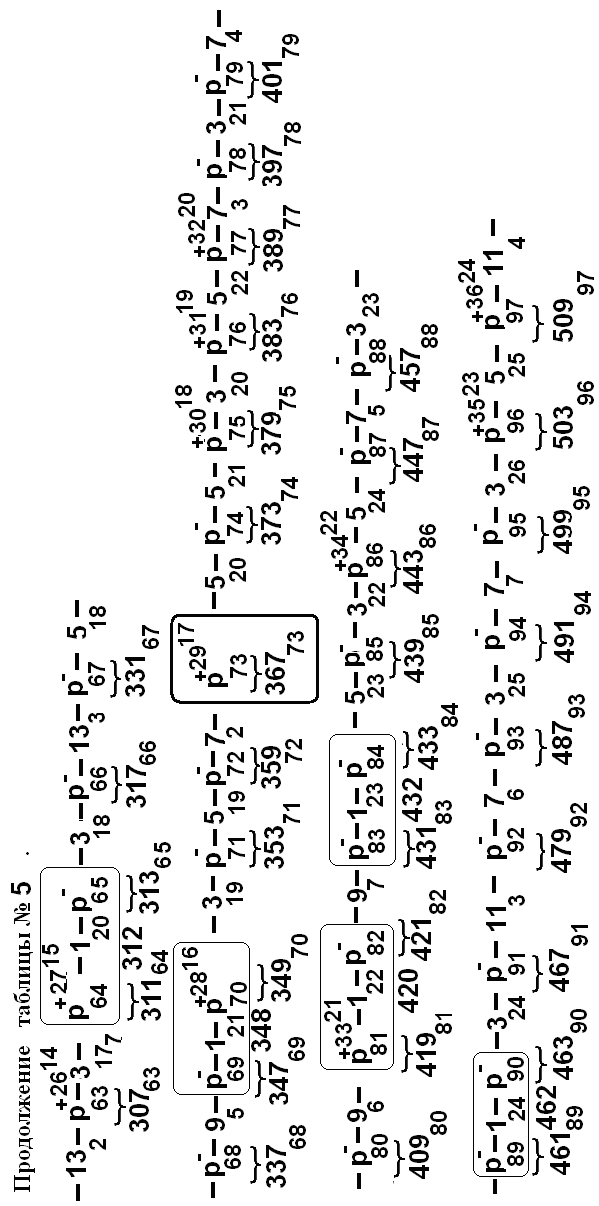
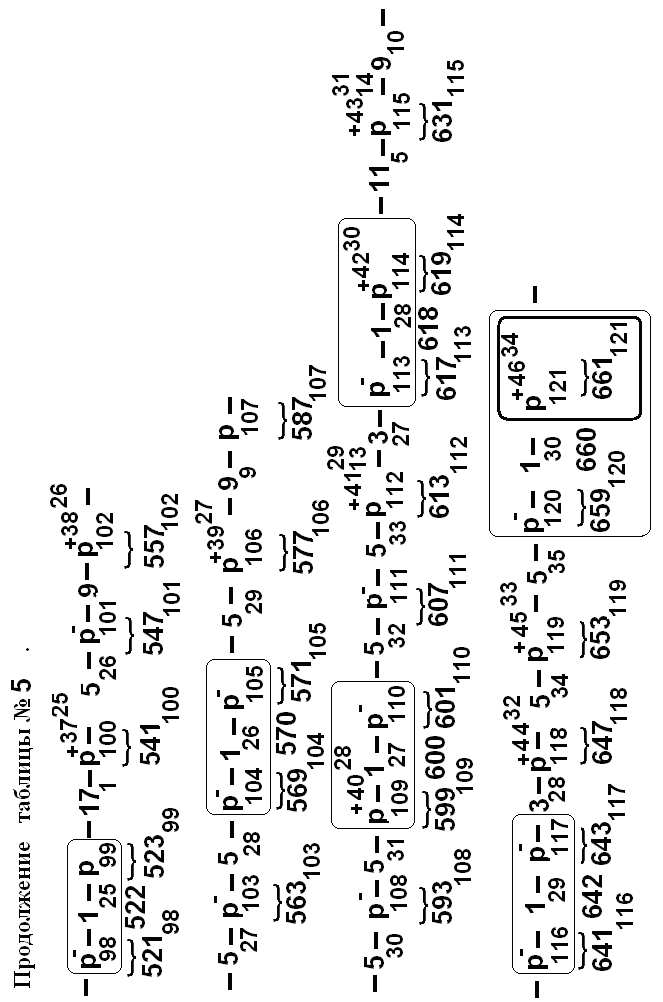
Р- и Р-Р- редукции – Таблицы №№ 1-5

Перейдем теперь к фиксации в виде таблицы процедуры

заявленной редукции, реализация которой почти элементарно сводится к её описанию (-параллельно с ним).

Во всех 2-ых столбцах таблицы N 1 расположены последовательные простые числа :

2_{1 ,}3₂ ,5₃ ,..-773₁₃₇₃₃ ,787_{138 ,}797₁₃₉₃₄ ,..,859₁₄₉₃₅ ,

а в первых – их порядковые номера. В ходе Р- редукции из784-ех последовательных номеров наступающих событий (вылупление происходит-опыт-на 850-й минуте, а последнее событие-деление на 784 (!) минуте,+/- 0,5 мин. (тоже(!)) были отобраны только простые последовательные числа с известными из опыта временами их наступления (-3-и столбцы). По выясненным, фиксированным опытным временам легко определяются их наилучшие приближения р-числами- 4-ые столбцы, в которых р-времена,

t^р= или

«кэт» в наших обозначениях –снабжены своими порядко-выми номерами (данные об этих парах содержатся в столбцах 1-2). В итоге, мы реализуем Р-Р-редукцию

В 5-ых столбцах содержится погрешность приближения опытных времен при их аппроксимации простыми числами.

В последних 6-ых столбцах приведены номера получив-шихся 57-ми р-р-пар, числа n в наших обозначениях

событий : N^p_t,.t^p_N ^{n 57} или «бра,кэт»ⁿ _.

Отметим, что изучение других вариантов, как равных именно 57-ми, так и других по величине, нами не проводилось. Оно может быть в дальнейшем реализовано по предлагаемой нами ниже общей схеме.

Специально подчеркнем, что указанное выше приближение простыми числами выполнено с неожиданно большой точностью. Соответствующий коэффициент корелляции равен

r = 0,99994541….

Получившиеся здесь четыре 9-ки, по сути дела, определили то направление, которому мы следуем в этом выпуске.

Этот результат показал, что р-р-приближение играет значительную роль в развитии нематоды, и особо важную – в самой быстрой, «взрывной» его части : её описывающие 34 времени из 57-ми событий представляют собой строго последовательный ряд простых р-чисел без пропусков -

……..

Эта область в таблице выделена горизонтальными скобками: к=47, 48, 49,50,..., 75, 76, 77, 78, 79,80.

Зафиксированная и отобранная нами 57-ка пар «коорди­нат» в р-р-представлении, событий делений и смертей клеток гермафродита нематоды С. Еlеgаns, несет в себе весьма примечательную информацию. В частности, это число-57-мь – является суммой корней диофантового уравнения в обратных квадратах по 7-ой шаг развития включительно и определяет пошаговый протокол динамики процесса универсального значения. Используемые при этом четыре корня на соответствующих шагах развития,-единственны (-и только они !). Только с 8-го шага начинается сильный рост числа решений, а на стадиях s=2,3,5 целочисленных решений не существует, но резко усилена дифференцировка. Добавив к числам 2,3,5 двойку и получив числа 4,5,7 имеем три размерности несуществующих полупростых алгебр Ли – факт, использованный нами в дальнейшем (стр. 67-69).

Итак, 57=1+4+36+16, s = 1,4,6,7. Используется модель с линейным ходом времени : ts = s ₀

Заметим, что во втором столбце таблицы выделено

проближение

, для которого и отвечает максимальной скорости роста и дифференцировки. Здесь

13 34-ке, а 25 57-ке

------------------

Итак .построенная таблица далее нуждается в модифи-кации : мы хотим оставить только искомый результат редукции - N^p_t,.t^p_N ^{n 57} или «бра,кэт»^n,-пары, причем в максимально компактной форме в виде пяти строк, средняя из которых имеет 13 р-р-скобок. Такая форма расположения позволяет обнаружить ценную закономерность : немного меняя численность р-р-пар в строках и слегка двигая строки относительно друг друга, можно поместить большинство р-номеров р-р-пар в 57-ке в вертикальных столбцах. Исключением оказались только три числа из 16-ти простых в 57-ке. Это Р_1,2,16 .

Последнее-16-ое, в пятой строке, поместилось в центре

(-на вертикале внизу) получившейся новой таблицы, над которым в вертикальном столбце находятся четыре составных числа, разделяющих также четыре близнеца, подряд идущих(пар) р-чисел.

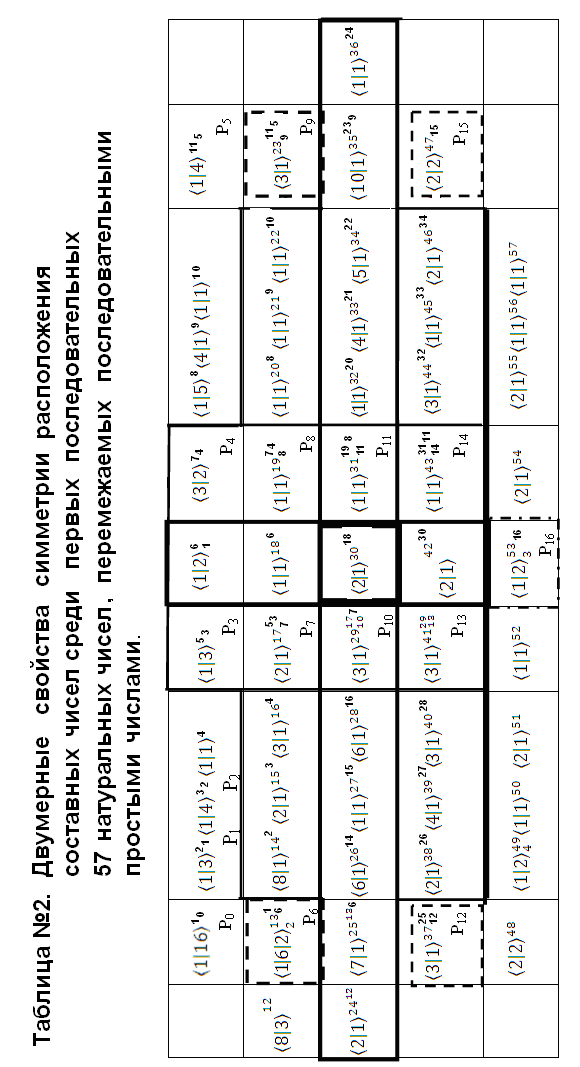
Ценность полученной формы (таблицы №2) представления первых 57 чисел натурального ряда («заготовка» для тора !!) состоит в том, что она визуализирует двумерные свойства симметрии расположения составных чисел среди первых последовательных 57-ми натуральных чисел, перемежаемых последовательными простыми числами.

Поясним, что в целях удобства, наглядности элементам таблицы временно придан упрощенный вид: в скобках

проставлены разности порядковых номеров-текущего и предыдущего-N и t р-чисел.

Таким образом, в весьма симметричном полученном («жирном» ) контуре («кладке») оказалось 34 р-р-числа.

* * *

π -Р-Р-аксиоматика и принцип Пигмалиона,

π - сигнатура

π -аксиома или аксиома Пигмаллиона -по нашему определению-состоит в изъятии всего «лишнего». Благодаря такой процедуре возникает или произведение искусства -мраморная скульптура прекрасной и затем ожившей Галатеи-жены ваятеля Пигмаллиона, либо, в нашем случае, достижение науки (гипотезы О.Б. и Р.О. Царёвых ). Подчеркнём, что для нас мифологическая компонента имеет прямой смысл: мы разрабатываем формализм, предназначенный для описания живых систем.

В ходе Р-редукции: [784х784] [57^рх57^р], или N^p_t,.t^p_N ^{n 57} , во-первых, не все простые порядковые номера среди 137-ми наличествующих до 784-го(-последнее это 773-е)событий делений клеток имеют опять же простое время, а во-вторых не все эти простые времена –их всего 57 штук-, а простых времён до 773-го события -95 (!!) поскольку последняя 57-я р-р-пара имеет вид

773^p₁₃₇,.499^p₉₅ ⁵⁷

Таким образом, оказываются «лишними» 137-57 = 80 номеров р-чисел, используемых в качестве номеров событий деления клеток, и 95-57 = 38 Р-чисел –опять «лишних», среди всех наличествующих за вычетом необходимых для перечисления, фиксации времен деления.

Итак, очевидна необходимость введения «π-сигнатуры» или системы знаков «+/-», используемых в качестве индексов оставляемых «+/» или удаляемых «/-» р-чисел или, иначе, не используемых в нашей модели части р- чисел.

Подчеркнем, что основная возникающая перед нами трудность это РАЗРАБОТКА ЭКОНОМНОЙ ИЛИ РАЦИОНАЛЬНОЙ АКСИОМАТИКИ, закладываемой в π -принцип.

Реализация этих «благих» намерений казуистична, сложна, она требует попеременного учета особенностей опыта, эксперимента и эстетики сложнейших отделов математики, к примеру, математической логики, теории чисел, теоретико-числовых аспектов алгебраической топологии и т. п. Отметим, что авторы довольно далеки до полного решения поставленных задач, хотя им можно претендовать на «контурные», или схематические подходы.

В прочем, см. стр.64 ниже, можно наметить вполне конструктивные шаги.

Итак, основным объектом нашего внимания будут как сами р-числа так и их наборы или фрагменты, находя-щиеся среди двух отрезков натуральногоряда: 57-ки и 137-ки. Подчеркнем, что р-числа во фрагментах должны обязательно иметь только последовательные, без пропусков, порядковые номера. Часть р-чисел и их фрагменты мы снабжаем знаком «+» - их мы оставляем, учитываем, а те, которые снабжаются знаком « - » -удаляются. Так возникающую систему знаков принято называть «сигнатурой». Именно неформальная фиксация определенной сигнатуры реализует нам

Р-редукцию:[784х784] [57х57]^р

и принцип Пигмаллиона,

В иллюстративных целях для упрощения введения необходимой лексики, её смысла, здесь мы приведём результат декомпактификации двух отрезков натурального ряда : 57-кии 137-ки, в которых они или

Таблица №1 приближений (r=0,99994541) простыми числами времен

1	2	3 (мин)	4	5	6	1	2	3 (мин)	4	5	6
1	2	50,0	5316	3	1	41	179	239,0	23952	0	186
2	3	68,1	6719	1.1	2	42	181	239,5	24153	1,3	197
3	5	84,1	8323	1.1	3	43	191	251,9	25154	0,9	208
4	7	89,4	8924	0.4	4	44	193	257,3	25755	0,3	219
5	11	102,7	10327	0.3	5	45	197	263,3	26356	0,3	2210
6	13	110,7	10929	1.7	6	46	199	265,0
7	17	124,0				47	211	267,4
8	19	124,5				48	223	269,1	26957	0,1	2311
9	23	124,8	12731	2.2	7	49	227	269,5
10	29	152,0	15136	1,0	8	50	229	271,5	27158	0,5	2412
11	31	152,6				51	233	272,1
12	37	152,9				52	239	273,1
13	41	153,4				53	241	273,3
14	43	153,6	15737	3,4	9	54	251	273,8
15	47	163,5	16338	0,5	10	55	257	274,3
16	53	182,3	18142	1,3	11	56	263	275,4
17	59	182,6				57	269	277,8	27759	0,8	2513
18	61	182,7	137р –ка			58	271	277,8
19	67	183				5917	277	278,2
20	71	183,2				60	281	278,5
21	73	183,3				61	283	278,6
22	79	184,4				62	293	279,1
23	83	185,4				63	307	281,6	28160	0,6	2614
24	89	196,6	19745	0,4	12	64	311	282,5	28361	0,5	2715
25	97	212,4	21147	1,4	131	65	313	283,7
26	101					66	317	284,1
27	103					67	331	289,4
28	107					68	337	290,0
29	109					69	347	291,0
30	113					70	349	291,0	29362	2,0	2816
31	127					71	353	295,6
32	131					72	359	296,7
33	1 37	222,8	22348	0,2	142	73	367	307,1	30763	0,1	2917
34	139	225,0				74	373	307,9
35	149	226,9	22749	0,1	153	75	379	310,2	31164	0,8	3018
36	151	227,3				76	383	311,9	31365	1,1	3119
37	157	227,9				77	389	316,6	31766	0,4	3220
38	163	229,5	22950	0,5	164	78	397	322,7
39	167	230,3				79	401	324,7
40	173	233,3	23351	0,3	175	80	409	330,2

н омеров(57опорных) событий делений и смертей клеток нематоды

1	2	3 (мин)	4	5	6	1	2	3 (мин)	4	5	6
81	419	331,1	33167	0,1	3321	121	661	410,0	40980	1,0	4634
82	421	331,4				122	673	416,8
83	431	335,5				123	677	420,9	42182	0,1	47
84	433	335,8				124	683	425,7
85	439	335,9				125	691	433,6	43384	0,6	48
86	443	336,1	33768	0,9	3422	126	701	444,4	44386	1,4	49
87	449	338,6				127	709	448,4	44987	0,6	50
88	457	341,4				128	719	455,3
89	461	341,5				129	727	456,6	45788	0,4	51
90	463	341,6				130	733	461,3	46189	0,3	52
91	467	341,7				131	739	466,7	46791	0,3	53
92	479	342,1				132	743	472,7
93	487	342,7				133	751	483,2	47992	4,2	54
94	491	344,8				134	757	484,8
95	499	346,5				135	761	488,6	48793	1,6	55
96	503	347,1	34769	0,1	3523	136	769	491,7	49194	0,7	56
97	509	347,7	34970	1,3	3624	13733	773	500,2	49995	1,2	57
98	521	350,7				138	787
99	523	351,9				13934
100	541	354,0	35371	1,0	3725		774	517,8
101	547	356,3					775	518,8
102	557	359,5	35972	0,5	3826		776	519,1
103	563	363,2					777	519,2
104	569	364,5					778	531,7
105	571	364,7					779	531,9
106	577	368,9	36773	1,9	3927		780	677,9
107	587	370,0					781	679,2
108	593	370,5					782	680,5
109	599	373,3	37374	0,3	4028		783	782,0
110	601	374,2					784	784,0
111	607	376,0				140	809
112	613	381,2	37975	2,2	4129	141	811
113	617	381,8				142	821
114	619	382,2	38376	0,8	4230	143	823
115	631	386,7	38977	2,3	4331	144	827
116	641	392,6				145	829
117	643	392,9				146	839
118	647	397,2	39778	0,2	4432	147	853
119	653	399,3	40179	1.7	4533	148	857
120	659	405,2				14935	859

меньшие этих чисел значения этого ряда снабжаются π-сигнатурой (см.стр.52-54, 63) ниже Таблицу 5₀). Одномерный вариант этой таблицы и в других обозначениях, более подробных, приводится нами на 5-ти страницах -55-62 в виде Таблиц №5,7.

* * *

Т Декомпактификация и

роль Р-чисел в фиксации симметрий

двумерного натурального ряда

(-отрезков в -57-137 чисел )

Напомним, что ранее, во 2 вып., на стр. 189, 192 и 193, на рисунках №№ 35, 36, (см. вып. 3, 234-235 с.) и особенно на 37-ом, мы, явно не акцентируя внимание, уже использовали «декомпактификацию», но тогда - оси действительных чисел с целью определения «периода» транзитивной группы или «кванта» времени с помощью 41-го 18-ти минутных и расположенных вертикально отрезков в 784-ти минутном большом интервале(-двувременной прямоугольник в качестве заготовки тора). Изображенный на Рис.37 ряд параллельных прямых, не только прямая регрессии, чей наклон связан с искомым периодом, но и «намотка» предполагаемого тора, компактифицируя который мы воспроизводим исходный отрезок в 784 мин. действительной оси времени.

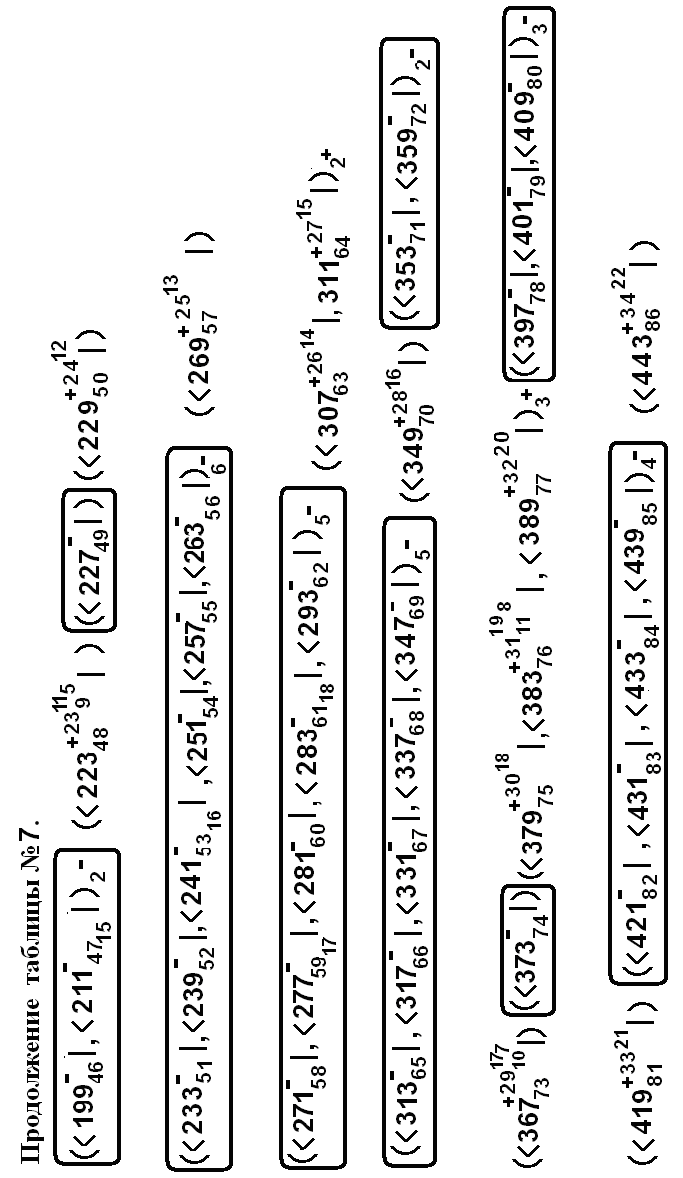
Пример реализации операции декомпактификации 57 и 137 целых чисел приведен в таблице( схемы А и Б ) № 8 этого выпуска. Причем, учет расположения Р-чисел немедленно при использовании данных опыта индуцирует введение π -принципа и π -сигнатуры.

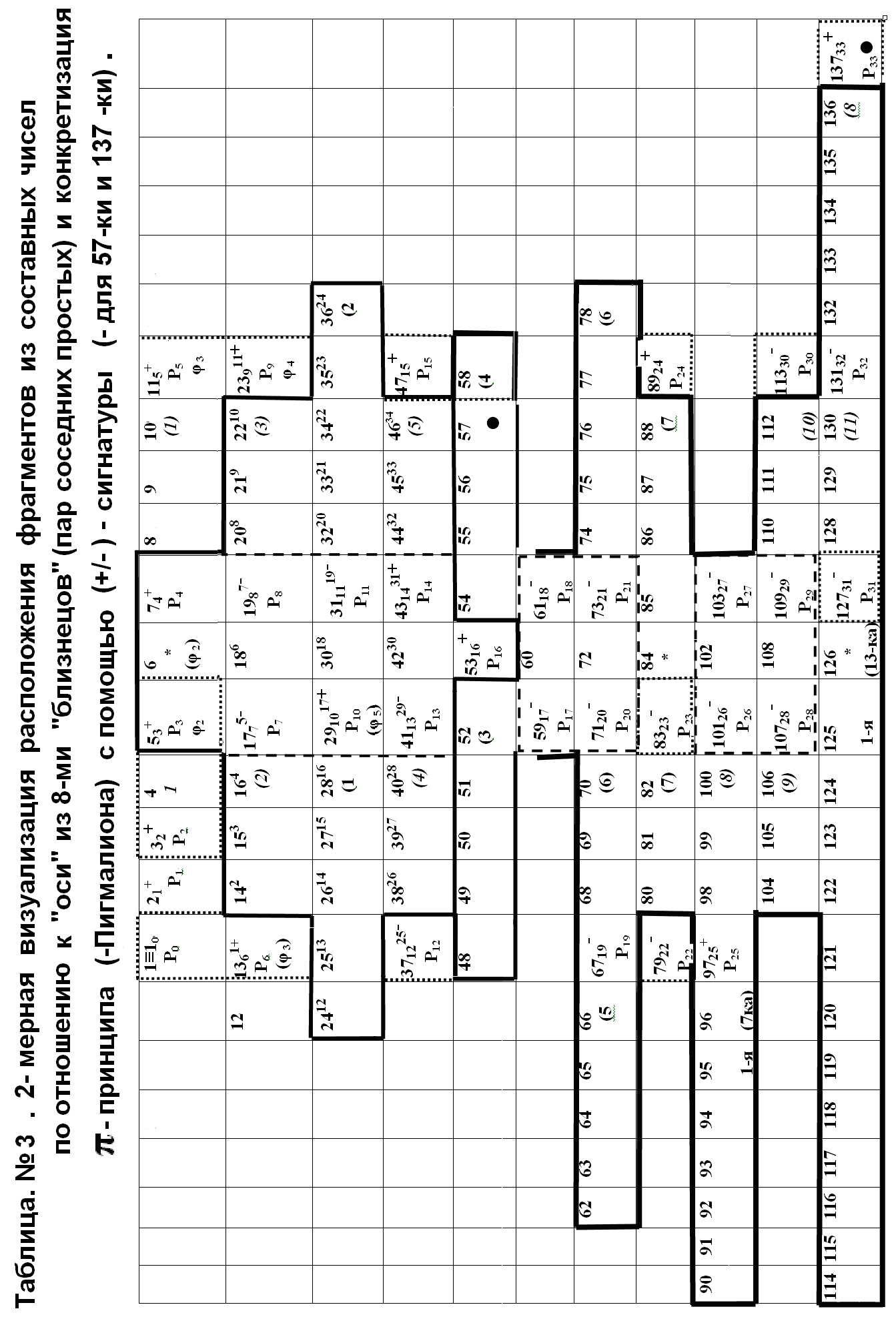
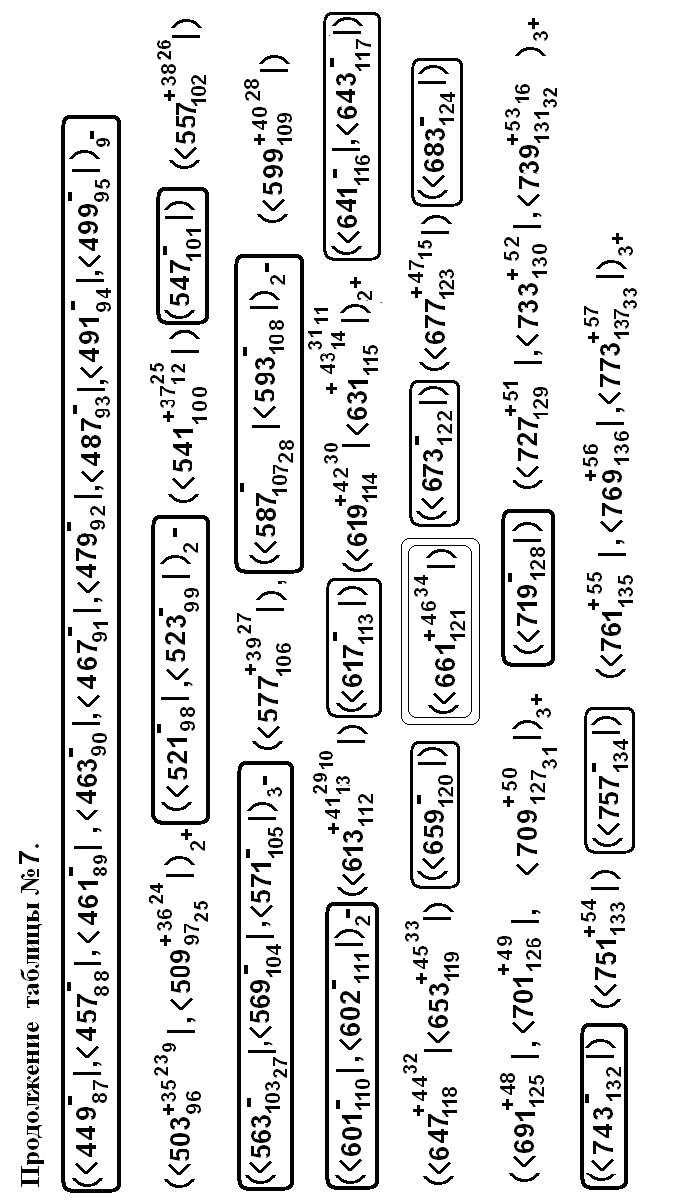
В иллюстративных целях, переходя сразу к результату этого замысла, мы обращаем внимание на явно выраженную симметрию на «ЁЛКЕ» –таблицы № 3 на стр.45 (см.выше): два столбца из р-чисел расположены параллельно парам р-чисел-близнецов, перемежаемые фрагментами составных чисел (-номеров простых (!)) длиною в (1),3, 5, 7, 13 чисел. Скобка (1) обозначает минимальный фрагмент длиною в одно составное число между последовательными р-числами. Эти (1)-скобки -8 скобок- по вертикали образуют ось симметрии на плоскости «декомпактифицированного» натурального ряда длиною в 773 минуты или 137-ым простым числом, которое само является 33-им р-числом. Далее, на «елке» скобками с левой стороны порядкового номера очередной 5-ки нами обозначены 5-ки последовательных составных чисел: (1, (2, и т.д. До момента времени 773 мин. их находится, 8 таких фрагментов, последний из которых, 8-ой представляет собой ряд из 132-го,133-го,134-го,135-го и 136-го простых (-по порядковому номеру) числа. Иначе, сами эти числа –простые, а их порядковые номера – составные. Напомним, что в таблице № 5₀ в верхних частях «строк» представлены номера n⁺- ых скобок N^p_t,.t^p_N ^{n 57} или <БРАIКЭТ>, где всегда под n понимается n⁺. Иначе говоря, мы таким способом вводим π–сигнатуру, или {+/}-сигнатуру в этом конкретном случае. Роль пар близнецов прерывается на 53₁₆ –ем простом, последним перед 57-ым, числе, приводя к нарушению осевой симметрии. Сравнительно идеальная «картинка» (-до 53-ех) далее нарушается всё чаще. Но выше упомянутые симметричные «столбцы» -левый-р₀, р₆, р₁₂, р₁₉, р₂₂, р₂₅ и правый-р₅, р₉, р₁₅, р₂₄, р₃₀, р₃₂ сохраняют свою «высоту»-число номеров- с разной последовательностью нарушений локальных симметрий по «вертикали».

Итак, этот пример позволил нам ввести определенную лексику и её трактовку с ценным функциональным смыслом.

* * *

Иллюстративное описание

аксиоматики π - принципа Пигмаллиона

(Краткое разъяснение схем А и Б таблицы № 5₀

в качестве примера)

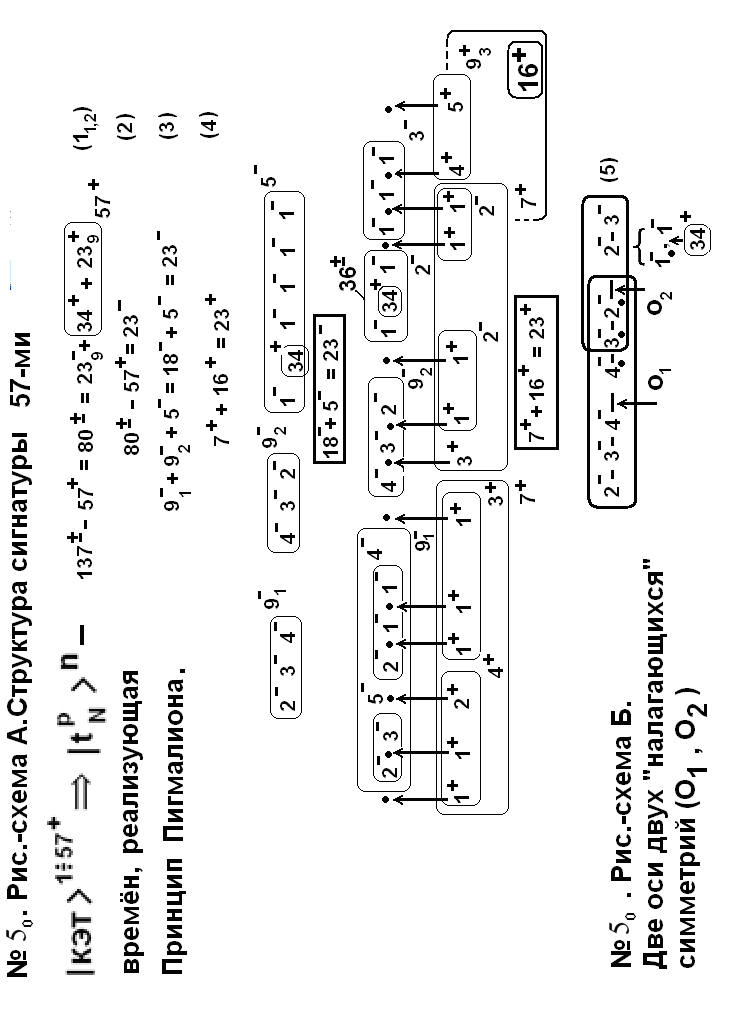
Таблице № 5₀ А,Б предшествует таблица №5₀ и её продолжение на следующей стр. 53 В качестве (весьма !) предварительной гипотезы или «аксиомы» мы приводим следующее разбиение 33-го простого числа 137 (в 4-ех «прямоугольниках») на 8- слагаемых :

137=[16₁+16₂]+[18₁+(18₂+1)]+[(18₃-1)+(18₄+1)]+[(16₃-1)+(16₄+1)].

При этом мы использовали кроме симметрично располо-женных 5-ти единиц 4-ре разных 16-ки и 4-ре разных 18-ки.

Очевидно, что такое разбиение получено из опыта, но в будущем предполагается разработка более прозрачной аксиоматики.

Отчасти, получившаяся симметрия флангов – 32 и 32 является следствием S-образности кривой накопления числа событий.

Выбираемая ниже π –сигнатура приводит к 57⁺ , если следовать «программе» продолжения Таблицы № 5₀, где подробно изложена процедура реализации π – принципа.

Причем, выше приведенное представление числа 137-ми несколько изменено: 137=16₁+16₂+18+19₁+17₁+19₂+15+17₂ . Это выражение заметно менее симметрично предыдущего (!), но более подробные преобразования при снабжении более «мелких» чисел и фрагментов {+/-}-сигнатурой приводят к весьма сложным и богатым симметрийным структурам. К примеру, слагаемое 17₂ представляется в виде :

17₂ [(1⁺, 1^-,1⁺), (1^-, 3⁺,1^-)]₈+

[(3⁺,1^-,1⁺,1^-,3⁺)]₉

Подчеркнем, что здесь как и в предыдущем слагаемом –в 15-ке-удаляются по 5 ти фрагментов. В сумме используемые 32⁺фрагмента составляют искомую 57⁺-ку.

Весьма примечательно, что возникающие «симмет-рийные» фигуры получены БЕЗ использования процедур ПОДГОНКИ- имеется ввиду БЕЗ перестановок слага-емых (!), считаем «приписывание» или канкатенацию некоммутативной арифметической операцией (- при используемом нами разложении в сумму (!)).

Напоминаем, что здесь и сейчас мы анализируем It^p_N ^{n 57}, IКЭТ , или времена событий. Схема В из таблицы № 5₀ более подробно фиксирует смысл снабжения сигнатурой 80-ти времен, из которых после вычета 23-ех остается 57 времен.

В итоге, можно четко констатировать – обнаружены весьма необычные симметрии сложной структуры. Их реальность гарантирована необычайно высоким коэффициентом корреляции «подгонки» простыми (см. 64-ю стр.)

числами опытных временных данных-4-ре девятки после запятой на 57–ми точках (!)

* * *

Добавим, что дальнейшая формализация алгеб-раического смысла обнаруженных симметрий натурального ряда, по-видимому, потребует продолжения процесса декомпактификаций до следующих порядков - 3-го, 4-го и т.д. и даже до произвольных n-ых порядков или размерностей. В лучшем случае, прояснение ситуации может прои-зойти уже на 3-ем или 4-ом порядке.

* * *

ГРУППЫ, АЛГЕБРЫ И

ИНВАРИАНТНОСТЬ S_n – СФЕР ,

ВЛОЖЕНИЕ (n – 1) – МЕРНЫХ СФЕР В

n – МЕРНЫЕ СФЕРЫ –

ИНДУКЦИЯ ДИХОТОМИИ ,

ПРОБЛЕМА ФОРМИРОВАНИЯ

УЛБТРА-АЛГЕБРЫ ТЬЮРИНГА

ИЛИ

«СИММЕТРИИ, РЕКУРСИИ, ДИХОТОМИЯ»

Н.Коперника…

об обращении небесных сфер…

…6 книг. 1543 г.

Здесь уместно прокомментировать последние успехи в доказательстве гипотезы А. Пуанкаре о гомеоморфизме и гомотопии n-мерным сферам широкого класса много­образий. На них может быть распространена при наделении их дискретными, целочисленными и многомерными качествами при соответствующих ограничениях вся наша идеология применения ДТА(см.с.168 вып.3).

Ближайшие страницы будут посвящены весьма примечательному факту – в нами выбранной теоретической схеме рекурсия s s+1 номера шага развития системы во времени индуцирует дихотомию трансформации клеток – деления и (-или) дифференцировки. Причем, эта индукция имеет топологическую природу, а описываемая логика перехода от рекурсии к дихотомии существенно подчинена групповым и алгебраическим свойствам инвариантности основного уравнения в обратных квадратах, чьи решения находятся на s-мерных единичных сферах евклидовых s+1-мерных пространств: s-мерная сфера делит s+1-мерную сферу всегда именно на две части (!), являясь при этом их гра-ницей (-«знаменитая» теорема Жордана-Брауэра «о разделении»: см.3,стр.49,лит.вып.III)/

1.Группа порядка [n(n+1)/2] c символами (-базисом группы см.6,стр.??,лит.вып.III)

p_i –xⁱ x^j p_j , xⁱ p_j - x^j p_i

(i,j = 1,….,n)

оставляет инвариантной сферу

(*)

и она( группа) –проста, если n ≠ 3 (6,cтр.224;Lie ,Engel,1893)

Заметим, что здесь сохранена лексика позапрошлого века.

Также напомним, что благодаря треугольной схеме суммирования случайных величин, полученные нами уравнения в обратных квадратах с решениями на сферах(см вып. I , стр. 39), содержат треугольную матрицу

X_sj j=s+1-i

с числом независимых элементов , равных

[s(s+1)/2]

для каждого шага развития s ,т.е. наши уравнения подчи­няются теореме Ли – Энгеля.

Итак, эта теорема ( п.1.,см. выше) и её обобщения (17,стр.98 и 221; лит. вып.III), а также теорема Жордана – Брауэра( см.выше) «о разделении» позволили нам существенно обобщить всю «идеологию» машин Тьюринга, представленной нами первоначально в виде восмиленточного протокола решения полной системы диофантовых уравнений ( 4,9,12-ая формулы, стр.46-48 и 125, вып.I) нашей модели развития. Ниже - таблицы NN -полная-784-392 и единственных полупростых групп Ли, размерностей их представлений - являются некоторым развитием первоначальных идей Тьюринга, обобщением возможностей тех алгебраических блоков, которые позволяют нам говорить об УЛЬТРА-АЛГЕБРЕ Тьюринга, над каждой s-ой клеткой которой «работает» новый алгебраический блок совершенно другой размерности и (или) «сорта» полупростой алгебры Ли, чем на шаг раньше. При этом саму исходную ячейку ленты машины Тьюринга мы можем делить на дополнительные строки-«ленточки» и «столбики»(-с собственными номерами развития, при необходимости компактифицируемых с помощью тора) на каждом шаге каждой ленты или «ленточки».

Очевидно, что такие «безбрежные» возможности должны

быть жестко «зааксиоматизированы»(хотя бы в будущем !). Ниже мы приводим несколько примеров таких конструкций, а также их реализации на примере классификации всех ныне известных элементарных частиц, а также примеры «работы нашей новой «УЛЬТРА –Т-машины»» при сопоставлении со свойствами 57-ки и её разбиений (см вып. I ,стр.50).Это сопоставление мы назвали А-разбиением. Смотри ниже стр. 78 .

Таблица.(полная 784-392).

									Bn=B2		Bn=B4		Bn=B5
B: s=2n+1 SO(s)									SO(5)		SO(9)		SO(11)
						Dn=D1						Dn=D5
D:s=2n SO(2n)						SO(2)						SO(10)
s-1	-2	-1	0	1	2	3	4	5	6	7	8	9	10
гр. LiS-1- полу- прост.				L1	L2	L3	-	-	L6	-	L8	L9	L10
n						1			2		4	5	5
Ранг под- ал.Кар- тана: r(s-3)= =s-3										-
						D1: 0, 1, 2			B2: 2		B4: 2	D5:
b:						2n-1= =C22n =1*2			2n=4		C(S1)/4=36	2n-1=16
s	-1	0	1	2	3	4	5	6	7	8	9	10	11
s-3		-3	-2	-1	0	1	2	3	4	5	6	7	8
-b	-0	-0	-1*1	-0	-0	-1*2	-0	-0	-4	-0	-36	-16	-1764
·b	+0	+0	+0	+0	+0	+0	+1	+0	+0	+1	+0	+0
2·a			2	2	4	8	14	30	60	112	226	380
2a+ b			2	2	4	8	15	30	60	113	226	380
aS		1	1	2	4	7	15	30	56	113	190	364
	+1*1	(1	2	3	5	9	16	31	61	117	230	420	784:2 =392

Таб.238-полная

									Bn=B2		Bn=B4		Bn=B5
B: s=2n+1 SO(s)									SO(5)		SO(9)		SO(11)
						Dn=D1						Dn=D5
D:s=2n SO(2n)						SO(2)						SO(10)
s-1	-2	-1	0	1	2	3	4	5	6	7	8	9	10
гр.Lis-1- полупрост.				L1	2L	L3	-	-	L6	-	L8	L9	L10
n						1			2		4	5	5
Ранг под- ал.Кар- тана: r(s-3)= =s-3										-
						D1: , 1,			B2: 2		B4: 2	D5:
b:						2n-1= =C22n= =1*2			2n=4		C(s-1)/4= =36	2n-1= =16
s	-1	0	1	2	3	4	5	6	7	8	9	10	11
s-3	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8
-b	-0	-0	-0	-1*	-0	-1	-0	-0	-4	-0	-36	-16	-1764
·b	+0	+0	+0	+0	+0	+0	+0	+0	+0	+0	+0	+36
2·a				2	2	4	6	12	24	40	80	88
2a+ b				2	2	4	6	12	24	40	80	124
as			1	1	2	3	6	12	20	40	44	108
s		+1*	(1	2	3	5	8	14	26	46	86	130	238)

Таб.42 полная

									Bn=B2		Bn=B4		Bn=B5
B: s=2n+1 SO(s)									SO(5)		SO(9)		SO(11)
						Dn=D1						Dn=D5
D:s=2n SO(2n)						SO(2)						SO(10)
s-1	-2	-1	0	1	2	3	4	5	6	7	8	9	10
гр.Lis-1- полупрост.				L1	2L	L3	-	-	L6	-	L8	L9	L10
n						1			2		4	5	5
Ранг под- ал.Кар- тана: r(s-3)= =s-3										-
						D1: , 1,			B2: 2		B4: 2	D5:
b:						2n-1= =C22n= =1*2			2n=4		C(s-1)/4= =36	2n-1= =16
s	-1	0	1	2	3	4	5	6	7	8	9	10	11
s-3	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8
-b	-0	-0	-0	-0	-1*	-1	-0	-0	-4	-0	-36	-16	-1764
·b	-0	+0	+0	+0	+0	+0	+1	0	+0	+3	+0	+0
2·a					2	2	2	6	12	16	38	4
2a+ b					1	2	3	6	12	19	38	4
as				1	1	1	3	6	8	19	2	(-12)
s			+1*	(1	2	3	4	7	13	21	40	42)

Поскольку наш протокол развития представляет собой восмиленточную

машину Тьюринга мы в его честь все-784-ые,238-ые и 42-ые супермультиплеты назовём супермультиплетами Тьюринга, а получающуюся благодаря уравнениям баланса эллиптического типа / /после многократного прямого удвоения и сложения весьма сложную алгебру, назовем ультра-алгеброй динамики Тьюринга:

{ А_Т^s}, s = -3,…,11.

_{Таблица единственных полупростых групп Ли и размерности всех их представлений.}

A n	. и :n+1: и :С2n+1, , и :Сin+1 SLn-вещественные гр.
B n	. :2n+1.С22n+1. , :Сi2n+1, , : Сn-12n+1, :2n.SO2n+1, спинорн.предст.,i<n для Bn
Cn	. :2n, :С22n-1, , :Сi2n- - Сi-22n, , :Сn2n-Сn-22n.Sp2n
D n	. :2n, :С22n, , :Сi2n, , :Сn-22n, и :2n-1.SO2n, спинорн. предст., i<n-1 для Dn. N- в СiN -размерность линейного представления
G 2	:7, :14
F4	:52, :1274, :273, :26
E6	и :27, и :351, :2925, :78
E7	:133, :8645, :365750, :27664, :1539, :56, :912
E8	:248, :30380, :2450240, :146325270, :6899079264, :6696000, :3875, :147250

Таблица открытых (на 1996 г.)

фундаментальных и элементарных -

взаимопревращающихся - частиц

(без кварков, но с X-Y , бозонами)

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
5(15)	(X - Y)				----
1		0		1-	----
1	Z0	91187(7)	2498(7)	1	----
2 =4	W+ W-	80150(100)	2250(140)	1	----
2	е е	8.10-6		1/2	----
2		0,27		1/2	----
2		31		1/2	----
2	е - е+	0,51099906 (15)		1/2	----
2	- +	105,658387 (34)	2,19703 (4)10-6	1/2	----
2 =12	- +	1777 (3)	295(3) 10-15	1/2	----

Таблица 35 -ти обычных мезонов( от до f₄ )

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
	+ -	139,5675(4)	2,603(2)•10-8	0-	1000
1	0	134,9739(6)	8,4(6)•10-17	0--	1000
1		548,8(6)	0,00119(12)	0-	0000
3	+ 0 -	768,3(5)	149,1(5)	1-	1000
1		781,95(14)	8,43(10)	1-	0000
1		957,5(2)	0,208(21)	0-	0000
3	а0+ а00 а0-	983(3)	57(11)	0+	1000
1		1019,412(8)	4,41(7)	1-	0000
3	b1+ b1 b1-	1233(10)	150(10)	1+	1000
1	f2	1274(5)	185(20)	2+	0000
1	0	1295(4)	35(6)	0-	0000
3	а2+ а20 а2-	1318,4(7)	110(5)	2+	1000
1	f1	1425(1)	55(3)	1+	0000
3	1+ 10 1-	1450(8)	237(16)	1-	1000
1	f2/	1525(5)	76(10)	2+	0000
1	1	1594(12)	100(30)	1-	0000
1	3	1668(5)	166(15)	3-	0000
1	1	1680(50)	150(50)	1-	0000
3	3+ 30 3-	1691(5)	215(20)	3-	1000
1	f //2	1713(2)	138(10)	2+	0000
1	3	1854(7)	87(25)	3-	0000
1, =35	f4	2049(10)	203(12)	4+	0000

_{Таблица 9-ти -и 12-ти} -мезонов

№	чс, ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
1	C	2980(2)	10(3)	0-	0000
1	J/	3096,93(9)	0,068(10)	1-	- -
1	С0	3451(1)	14(5)	0+	- -
1	С1	3510,6(5)	<1,3	1+	- -
1	С2	3556,3(4)	3(1)	2+	- -
1		3686,0(1)	0,243(43)	1-	- -
1		3770(2)	0,24(3)	1-	- -
1		4159(20)	78(20)	1-	- -
1	= 9	4415(6)	43(15)	1-	- -
1	Υ	9460,32(22)	0,052(2)	1-	- -
1	b0	9860(1)	?	0+	- -
1	b1	9891,9(7)	?	1+	- -
1	b2	9913,2(6)	?	2+	- -
1	Υ /	10023,3(3)	0,043(8)	1-	- -
1	b0	10235(1)	?	0+	- -
1	b1	10255,2(4)	?	1+	- -
1	b2	10269(1)	?	2+	- -
1	Υ//	10355,3(5)	0,024(3)	1-	- -
1	Υ///	10580(3)	24(2)	1-	- -
1	Υ////	10865(8)	110(13)	1-	- -
1	=12 Υ/////	11019(8)	79(16)	1-	- -

_{Таблица 32-х странных, 20-ти очарованных и}

_{4-х прелестных мезонов.}

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
2	К+ К-	493,646(9)	1,2371(29)10-8	0-	1/2100
2	К0 =5,17(4)·10-8	497,67(3)	= 0,8922(29)10-10	0-	- -
4	К*+ К*0 К*-	891,8(2)	49,8(8)	1-	- -
4	К+1 К01 К-1	1210(10)	90(20)	1+	- -
4	К/+1 К/01 К/ -1	1402(7)	174(13)	1+	- -
4	К*+2 К*02 К*-2	1425(1)	98(2)	2+	- -
4	К+2 К02 К-2	1768(14)	136(18)	2-	- -
4	К*+3 К*03 К*-3	1774(8)	164(17)	3-	- -
4	К*+4 К*04 К*-4	2045(9)	198(30)	4-	- -
2	D+ D-	1869,3(4)	10,62(28)10-13	0-	1/2010
2	D0	1864,5(5)	4,2(1)10-13	0-	- -
2	D*+ D*-	2010,1(6)	<1	1-	- -
2	D*0	2007(1)	<2	1-	- -
4	D+1 D01 D-1 1	2424(6)	20(5)	1+	- -
4	D+2 D02 D-2 2	2459(2)	19,(7)	2+	- -
2	D+s D-s	1968,8(7)	4,4(3)10-13	0-	0110
2	D+s1 D-s1	2536,5(8)	4,6	1+	0110
2	B+ B-	5278,8(4)	1,6(1)10-12	0-	1/2001
2	B0	5278,8(3)	1,5()10-12	0-	1/2001

Таблица 104-х обычных барионов(p,n,N, :2+2+36+64)

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
2	p	9 38,2723(28)>5·1032лет		1/2+	1/2 000
2	n	939,56563(28)889(3),сек		1/2+	- -
4	N+1 N01 N-1	1440(20) 200		1/2+	- -
4	N+3/ N03/ N-3/ /	1520(10) 125		3/2-	- -
4	N+1/ N01/ N-1/ /	1650(30)	150	1/2-	- -
4	N+5 N05 N-5	1680(10)	125	5/2+	- -
4	N+3// N 03// N-3// //	1700(30)	100	3/2-	- -
4	N+3 N03 N-3	1720(30)	200	3/2+	- -
4	N+7/ N07/ N-7/ /	2190(40)	350	7/2-	- -
4	N+9 N09 N-9	2220(70)	300	9/2+	- -
4	N+11 N011 N-11	2600(60)	400	11/2-	- -
8	++ + 0 - ++ + 0 -	1232(2)	115	3/2+	3/2 000
8	++1/ +1/ 01/ -1/ ++1/ +1/ 01/ 1/	1620(20)	140	1/2-	- -
8	++3/ +3/ 03/ -3/ ++3/ +3/ 03/ -3/	1700(70)	250	3/2-	- -
8	++5 +5 05 -5 ++5 +5 05 -5	1905(70)	300	5/2+	- -
8	++3 +3 03 -3 ++3 +3 03 -3	1920(60)	250	3/2+	- -
8	++5/ +5/ 05/ -5/ ++5/ +5/ 05/ -5/	1930(40)	250	5/2-	- -
8	++7 +7 07 -7 ++7 +7 07 -7	1950(40)	240	7/2+	- -
8	++11 +11 011 -11 ++11 +11 011 -11	2420(40)	300	11/2+	- -

Таблица 86 странных барионов( _{1, 3, 1, ,} :

20+12+36+8+8+2 )

№	чс,ист.ней,.ант.чс	м0,МэВ		,сек.МэВ	JP	ISCb
2		1115,63(5)		2,63(2)·10-10	1/2+	0,-1,0,0
2	1/ 1/	1405(5)		50	1/2-	- -
2	3/ 3/		1520(1)	16(1)	3/2-	- -
2	1// 1//		1670(10)	35	1/2-	- -
2	3// 3//	1690(5)		60	3/2-	- -
2	1 1	1810(50)		150	1/2+	- -
2	5 5	1820(5)		80	5/2+	- -
2	3 3	1890(30)		100	3/2+	- -
2	7/ 7/	2100(20)		200	7/2-	- -
2	9 9	2350(10)		150	9/2-	- -
2	+ +	1189,37(7)		0,799(4)·10-10	1/2+	1,-1,0,0
2	0 0	1192,5(1)		7,4(7)·10-20	1/2+	- -
2	- -	1197,43(6)		1,48(1)·10-10	1/2+	- -
2	+3 +3	1382,8(4)		35,8(8)	3/2+	- -
2	03 03	1384(1)		36(5)	3/2+	- -
2	-3 -3	1387,2(5)		39(2)	3/2+	- -
6	+3/ 03/ -3/ +3/ 03/ -3/	1670(15)		60	3/2-	1,-1,0,0
6	+1/ 01/ -1/ +1/ 01/ -1/	1750(30)		90	1/2-	- -
6	+5/ 05/ -5/ +5/ 05/ -5/	1775(5)		120	5/2-	- -
6	+5 05 -5 +5 05 -5	1915(15)		120	5/2+	- -
6	+3// 03// -3// +3// 03// -3//	1940(40)		220	3/2-	- -
6	+7 07 -7 +7 07 -7	2030(15)		180	7/2+	- -
2	0 0	1314,9(6)		2,90(9)·10-10	1/2+	1/2,-2,0,0
2	- -	1321,3(1)		1,64(1)·10-10	1/2+	- -
2	03 03	1531,8(3)		9,1(5)	3/2+	- -
2	-3 -3	1535,0(6)		10(2)	3/2+	- -
4	03/ -3/ 03/ -3/	1823(5)		24(10)	3/2-	- -
4	05 -5 05 -5	2025(5)		20(5)	5/2?	- -
2	- -	1672,4(3)		0,82(1)·10-10	3/2+	0,-3,0,0

Таблица 16-ти очарованных (14: ) и

прелестных барионов (2: )

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ	JP	ISCb
2	с+ с+	2285(1)	1,9(1) 10-13	1/2+	0010
6	+с 0 с	2453(1)	?	1/2+	1010
2	+с +с	2469(2)	3(1) 10-13	1/2+	1/2,-110
2	0с 0с	2467(2)	1·10-13	1/2+	1/2,-110
2	-с -с	2706(3)	?	1/2+	0-210
2		5620(30)	1,0(2)·10-12	1/2+	000-1

Таблица предсказываемых 58-ми ещё не-открытых t-кварковых частиц:«правдивых» мезонов и барионов

№	чс,ист.ней,.ант.чс	м0,МэВ	,сек.МэВ		JP		ISCb
1		?	?		---		--
2	+t -t	?	?		---		--
2	0t 0t	?	?		---		--
2	-t +t	?	?		---		--
2,	*0t *0t	?	?		---		--
8	++t +t t0 t- ++t +t t t-	?	?		---		--
6	·	?	?		---		--
4	*-t *0t *-t *0t	?	?		---		--
2, =20 =29.	-t -t	?	?		---		--
в s , =6	+t -t	?	?		---		--
в s =6	0t 0t	?	?		---		--
в s , =5	0t 0t	?	?		---		--
в s , =4	0t 0t	?	?		---		--
2	+t -t	?	?		---		--
2	++t --t	?	?		---		--
2	+t -t	?		? ---		--
2, =29 =58	0t 0t	?		? ---		--

Таблица соответствий 7-ми ПРЯМЫХ СУММ спинорных представлений супермультиплетов в пространстве Калаби-Яу наблюдаемым 334-м и предсказываемым 58-ми t- кварковым правдивым частицам (без учета самих, кварков и X-Y- бозонов).

Согласно модели ДМЯ, решения на 4-м,6-м и 7-м шагах развития при выбранном изоморфизме отвечающие сворачиваемым размерностям при компактификации, разбиваются на следующие слагаемые.

4₀ⁱ = 1₀ⁱ + ·1₀ⁱ + 1₀ⁱ + 1₀ⁱ = 2₀ⁱ + 2₀ⁱ .

36ⁱ = 9₁ⁱ + 9₂ⁱ + 9₃ⁱ + 4₁ ⁱ + 4₂ ⁱ + 1 ⁱ

16ⁱ ₌ 4₁ⁱ ₊ 4₂ⁱ ₊ 4₃ⁱ ₊ 1₄ ⁱ ₊ 1₄ ⁱ ₊ 1₄ ⁱ ₊ 1₄ ⁱ

^{i= .} 4₀ⁱ+36ⁱ+16ⁱ)=

=А¹+А²+А³+А⁴+А⁵, где

А⁵ А⁵_{(6+ )(16-4)=(6+ )( + + )=А}⁵_0+А⁶_+А⁷.

_А⁵₀=(5+ )(4₁+4₂+4₃)=( ·4₁)+

+( )+5·(4₁+4₂+4₃).

_А⁶_=А⁶_{( ) ( ) ;А}⁷_{( )=( )t=8t.}

_Далее.

А¹ А_{7(40+1 )}=35_{( )}=

=7(2+(2+1 ))=7·2₀+7·3₀=

=2 +2 + 2 +2 +2 +2 +2 +

+3 +3 +3 +3 +

+3 +3 +3

А²_7·36=36 +36_N+ А²_5·36;

А²_5·36=(1+3+ )·(9₁+9₂+9₃+9₄)=

·(9₁+9₂+9₃+9₄)+(1+3) (9₁+9₂+9₃+9₄)=

= ·(9₂+9₃+9₄)+1·9_{1(с ) очар.мезоны}+

+1·(9₂+9₃+9₄)_t+3·(9₁+9₂+9₃+9₄) =

= а₁+а₂+а₃+а_4.

а₁= а_1(1·36)=(9₁+9₂)+(9₃+9₄)=16 +2 +

+(4₁ +4₂ )+1₃+(4₁ +4₂ )+1₄=

=16 +2 +14₍ +2 +(2_3,4)_t

а₂=9_{1(с ) очар.мезоны}; а₃=(а₂₇)_t; а₄=а₁₀₈.

а₁₀₈=3·(9₁+9₂+9₃+9₄)+3·(1 ₊1 ₊1 ₊1 )+

+3(16_1,2+16_3,4)=12_t+3·16_1,2+1·16_3,4+2·16_3,4=

=12_t+64_1,2,3,4+32_3,4=12_t+64 +32₍

А³=А³_3(16-13)=3·(1_{4 +}1_{4 +}1_{4 )=9t}

А⁴=А⁴_4(1613)=4·( _{4 + 4 + 4 )=12(лептонов)}

_А⁵₀=(5+ )(4₁+4₂+4₃)=( ·4₁) +

+( )_t+5·(4₁+4₂+4₃).

_А⁵₅=5·(4₁+4₂+4₃)=(1+4) (4₁+4₂+4₃)=

=1·4₁+1·4₂+(1·4₃+4·4₃)+4·(4₁+4₂)=

=4_p,n+4_B(прел)+20_{D(очаров)}+32_{К(стран)} в₃

_А⁵₀=(5+ )(4₁+4₂+4₃)=в₁+в₂+в₃

в₁=( ·4₁) ; в₂+ _А⁶_{( )} в₂+ _{( )=}

=12 _{-мезоны}

_{Баланс 58 ещё не открытых, но «расквартированных» t-кварковых, правдивых}

_{частиц: 2+27+12+9+8=58 - на предыдущей -130-ой странице - все эти числа помечены буквой t}

_{* * *}

Вернемся к таблице №4. Имеет смысл обратить внимание на « философию» матриц-функций < БРА,КЭТ >

БРА I КЭТ

Р-редукция:[784х784,0 мин.] [57х57]^р

Или

N^p_t, t^p_N ^{n 57-ке} -редукция и логика

взаимоотношений пространства - времени

Г. ЛЕЙБНИЦА

У Владимирова ( 1,стр.155, вып, III) со ссылкой на Э.Маха, опиравшегося на взгляды И.Ньютона, подчеркнуто : «для Ньютона время и пространство суть ПЕРВИЧНЫЕ, незави симые переменные, направляющие и регулирующие все в мире.

При таком взгляде мир становится ОРГАНИЗМОМ(или- «машиной»-при огрублении –авторы, Царёвы).

Далее приводится ссылка и на самого Г. ЛЕЙБНИЦА :

«Я неоднократно подчеркивал, что считаю пространство, так же как и время, чем-то чисто относительным (по отношению к друг другу): ПРОСТРАНСТВО–ПОРЯДКОМ СУЩЕСТВОВАНИЯ, А ВРЕМЯ–ПОРЯДКОМ ПОСЛЕДО­ВАТЕЛЬНОСТЕЙ (СОБЫТИЙ). Авторы трактуют это высказывание следующим образом : БРА I – это – пространство, а I КЭТ - время, поскольку для нас порядок существования –это НОМЕР СОБЫТИЯ в ряду других событий, каждое из которых по Лейбницу и есть, определяется, порядком ПОСЛЕДОВАТЕЛЬНОСТЕЙ (СОБЫТИЙ) или, тем самым, является ВРЕМЕНЕМ (!!!) .В итоге мы, «играя» лексикой и словом «первичный» (на польском языке, у В.Серпинского это –ПРОСТОЕ число) трансформируем координацию «последовательностей (событий)» в символ-матрицу БРА I КЭТ ⁿ или в скобку N^p_t, t^p_N ^{n 57-ке} , в которой и время, и его порядковый номер для отобраных 57-ми (Р-Р) - пар являются простыми числами с высокой кореляцией с опытными данными( временами делений и смертей клеток нематоды, с коэффициентом корреляции r=0,99994541 …( 4 ре девятки !! на 57-ми числах)..приближений к опытным значениям времен).

Непосредственно из твблицы №4 вытекают довольно много соотношений симметрий, которые мы сведем в несколько таблиц

Т аблица (11) . А) Начало «таблицы-лесенки» «горизонтальных» симметрий (N, t_p)ⁱ (t_p, t_q )^k и Б) 14 в сумме (непрерывных 11, k k+1, 56 -66) «горизонтальных» симметрий.

А)

Б)

I

Таблица N12. 14-ть ступенчатых симметрий и

суперкомпозит .из 14-ти компонент.

Таблица (9) 14-ти непрерывных(почти) по индексу 2-го порядка- (-k-го) «номера n_k р-го числа»: - чисел среди 57-ми опорных, где «квадратик» □ означает возможную «глубокую» иерархию индексов – до пяти и более.

14-ка( ): последовательные номера в числах (n=3)

- общая форма записи эл-тов 14-ки ( ).

- здесь нумератор элементов 14-ки с возможным

«спуском в квадратик»

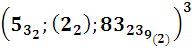
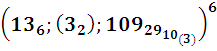
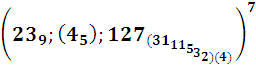
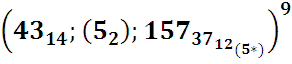
(13), (14) – отсутствуют.

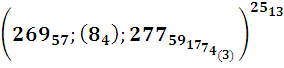
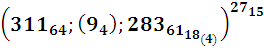
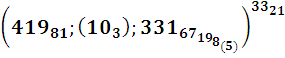
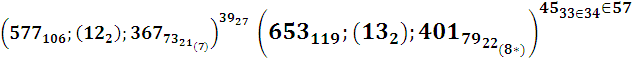
(23-я)- отсутствует

8, 9, 10, 11, 12 (-5 шт.) 15, 16, 17, 18, 19, 20, 21, 22 (-8 шт.) +24

Отметим, что 5 и 8 – последовательные числа Фибоначчи.

14-ка схожа с 34-ой : и там и там существуют ряды подряд следующих номеров простых чисел , только 34-ка-идеальна – без пропусков, а 14-ка имеет 3 пропуска 13, 14 и 23.

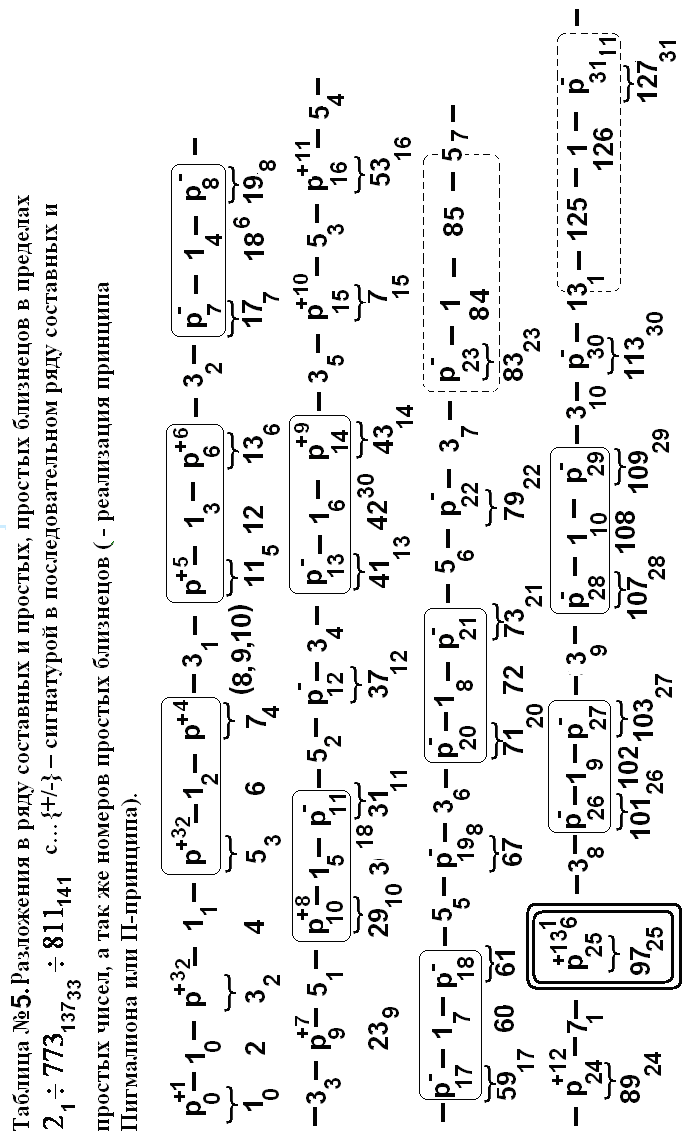
ТАБЛИЦА N 34-х простых пар чисел или событий:

N^p_t, t^p_N ^{n 57-ке} Числа n^q = 13 ¹,14 ²…45³³ , 46³⁴ .

Р^t =р₄₇, р₄₈ ..р₇₉,р₈₀ .к=47-:- 80. Отметим, что простые

N^pm =97₂₅ -661 ₁₂₁этим свойством и в том же или меньшем объёме не обладают за исключением отрезка в 6 или еще меньших чисел.

q	N	m	t	k	q	N	m	t	k
1	97	25	211	47	18	379	75	311	64
2	137	33	223	48	19	383	76	313	65
3	149	35	227	49	20	389	77	317	66
4	163	38	229	50	21	419	81	331	67
5	173	40	233	51	22	443	86	337	68
6	179	41	239	52	23	503	96	347	69
7	181	42	241	53	24	509	97	349	70
8	191	43	251	54	25	541	100	353	71
9	193	44	257	55	26	557	102	359	72
10	197	45	263	56	27	577	106	367	73
11	223	48	269	57	28	599	109	373	74
12	229	50	271	58	29	613	112	379	75
13	269	57	277	59	30	619	114	383	76
14	307	63	281	60	31	631	115	389	77
15	311	64	283	61	32	647	118	397	78
16	349	70	293	62	33	653	119	401	79
17	367	73	307	63	34	661	121	409	80

Рис 1. График области самого интенсивного роста: