В формулах (11-16) параметры связаны так:

(17)

, где (18)

(19)

(20)

Теперь еще раз напомним, что ф-ла Леви учитывает как непрерывные, так и скачкообразные компоненты случайной величины с произвольной величиной скачков, ибо, например, закон Гаусса порождается только непрерывными процессами, а закон Пуассона скачко­образным, у которого скачки кратны только одной вели-чине u₀ 0. Итак, константы с_1,2 и показатель фиксируют вид двух распределений величин скачков

в (11) случайной величины . Для закона Коши

=1 и с₁=с₂=С

Добавим, что в самих плотностях распределений, кото-рые являются непрерывными функциями, исходная скачкообразность и наличие тех или иных компонент в случайных величинах - дискретных, скачкообразных, сингулярных или непрерывных- исчезает, а сами «меха-низмы», их нивелирующая роль в «слиянии» в единую аналитическую форму, составляют предмет основ теории, причем в познавательном и прикладном смысле раскрытие этих «механизмов» зачастую приносятся в жертву «математической доказательности» и экономности изложения, оставаясь скрытыми, «за кадром» наглядного обозрения. Поясним вышеупомянутое разложение произвольного распределения на компоненты.

Пусть а₁+а₂+а₃=1, тогда существует единственное представление для любой функции распределения F(x)и такое, что F(x)= а₁F₁(x) + а₂F₂(x) + а₃F₃(x), а F₁(x), F₂(x), F₃(x) - функции распределения также.

Здесь F₁ (х)-абсолютно непрерывное распределение и f(x)=F^/(x) почти всюду, а F₃ (x) - чисто скачкообразная компонента, тогда как F₂ - распределение, без скачков и почти всюду F₂^/ (x)=0. F₂ сосредоточено на несчетных множествах, оно непрерывно, но не абсолютно. Его точки роста образуют меру нуль по Лебегу.

Отметим еще одно важно свойство устойчивых рас-пределений. Т.к. они порождаются аддитивностью слу-чайных величин, то суммам этих величин отвечают простые распределения, в которых также обладают ад-дитивностью их параметры. Например, параметры рас-пределения Гаусса - средние и дисперсии: если у двух законов q₁(x-a; ) и q₂(у-b; ) средние и дисперсии соответственно равны а, b и , , то у суммы Х+Y=Z будет распределение q₃[z-(а+b);( + )] со средним а+b и дисперсией + . Аналогично и у закона Коша пара-метры и являются аддитивными. Т.е. если

; , то

, где s = a + b, S = A + B.

При несколько иной параметризации этого закона

,

складываются обратные значения параметра , т.е.

1/ ₀ =1/ ₁ +1/ ₂

Оба закона - Гаусса и Коши - обладают в силу этого удоб-ной при построении вероятностных бумаг масштабной инвариантностью по обеим осям, что наглядно демон-стрируется представлением

Оба распределения колоколообразны и имеют в соот­ветствующей отнормированной форме две общие точки пересечения - в нуле и при х/ 1,987, / 0,7979; оба при 0 и 0 превращается в дираковскую дельта-функцию. Наконец, отметим :

.

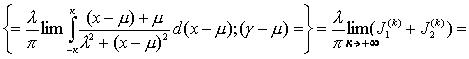
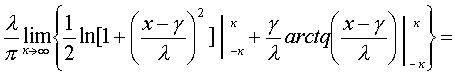
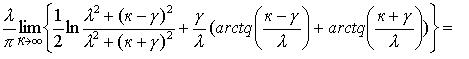
Наконец, самое важное следствие скачкообразности процессов, порождающих распределение Коши, это от-сутствие второго момента - он расходится, у распреде-ления Коши дисперсия бесконечна [25, Л-1].

По нашему мнению [12, Л-1] дисперсия есть мера мик-рогетерогенности значений исходной случайной вели-чины, ибо закон Гаусса и все распределения с конечной дисперсией имеют быстро спадающий хвост, для закона Гаусса f(x) ~ , x → ∞, тогда как для Коши - обратно пропорционально квадрату, т.е. х^--2 при x → ∞, Это свой-ство и отсутствие дисперсии вынуждает нас принять, что закон Коши или в асимптотике 1/x² - распределение по обратному квадрату - отражает макрогетерогенность значений рассматриваемой «случайной» величины.

Именно в применении к биологическим объектам весьма неестественно говорить о стремлении к бесконечности объема выборки, и невозможно при этом сохранить требуемую однородность и репрезентативность, аналогичную исходной малой выборке. Таких выборок в природе нет и даже в абстракции их существование гораздо менее правдоподобно, чем, скажем в физике или астрономии. А без обращения к предельным значениям и к возможности их повторного воспроизвод-ства невозможно говорить о самом понятии «частота» или «вероятность». По-видимому, именно подобные обстоятельства побудили А.Н. Колмогорова ввести алгоритмическое определение вероятности, а затем и сложности алгоритма [29-30, Л-1] , тесно связанные с частотным подходом в основах теории вероятности и теории информации.

В заключение этого раздела приведем некоторые све-дения об уже упоминавшемся распределении ЦЛП. Сама плотность и распределение при х< и

при

х . Причем, если >1, то =Мх=( ) . Это распределение не относится к классу устойчивых. Далее, упоминая распределение Коши, мы будем использовать безразмерную и неотнормированную плотность

(21)

Забегая вперед и анализируя необычайную эффектив-ность модели [7, Л-1], можно сейчас в дискуссионном по-рядке предположить, что требование диофантовости решений основного уравнения в обратных квадратах компенсирует отсутствие устойчивости у фактически использованного распределения Парето (по [7, Л-1] -рЦЛП ). Действительно, рЦЛП имеет особенности в нуле, которой нет ни у закона Гаусса, ни у закона Коши. Особенность появляется при х=0 у устойчивых распределений лишь при →0 [26, Л-1]. Но требование диофантовости [7, Л-1]. исключает особенность в нуле, поскольку в этом случае х не может стремиться к нулю.

Исходя из этого дискуссионного сопоставления мы надеемся, что в ближайшем будущем удастся обобщить операцию свертки в применении к «проквантованному распределению» Парето и к многочисленным корням уравнения (6) при s>>1. Обобщить так, что с помощью специфического отбора решений можно будет ввести аналог устойчивости и для такого «Парето», но на диофантовом подмножесве множества корней уравнения (6), см. ниже.

Подобный результат весьма заметно усилил бы обос-нованность модели, поскольку апелляция к асимптоти-ческому варианту закономерности Коши плохо работает именно в начале этапа развития, который, тем не менее, нашел аргументированное подтверждение.