14. Наибольший общий делитель

(НОД).

1. Весьма важную роль в окончательном завершении нашей программы на уровне теорем существования будет играть многочлен

f(x)=НОД(f(x),хⁿ-1) в К[x] (61)

Если f( ) - циклическое отображение, то

f( ) = t( ) = (1 - e_t( )) (62)

Здесь выражение 1 - e_t( ) - является циклической проекцией, имеющей с отображениями f( ) и t( ) образ и ядро. Т. е. если R - кольцо главных идеалов и m R

- свободен от квадратов, то отображение -

t( ) Кer t( ) (63)

задает изоморфизм структуры делителей многочлена

хⁿ-1 (64)

на булеву алгебру циклических классов n-угольников.

Или

Кer t( )=Кer t((1 - (1 - e_t( )) = Im e_t( ) (65)

2. Пусть элемент m 0 кольца главных идеалов r представим в виде произведения попарно взаимно простых элементов:

m=t₁ , t₂, ... , t_k (66)

тогда существует смежные классы

e₁+(m); e₂+(m); ... ; e_k+(m) (67)

со свойствами

а) смежные классы (61) попарно ортогональны, а их сумма является смежным классом единицы.

б) (t_i + (m))=(1- e_t(i)+(m)) (68)

Далее принимаем, что e_t(i) e_i .

Поскольку (t+(m))=(1- e_t+(m)) и можно принять, что

-197-

(t+(m)) и (e_t(i)+(m)) - (69)

взаимно дополнительные идеалы в R/(m).

Итак, равенство (61) со свойствами а) и б) ознает, что мы получим композиционный ряд (!) (см. более подробно о реализации рядов Галуа ниже)

Подчеркнем, что компоненты композиционного ряда Галуа (67) и информация о с-коэффициентах n-угольников вводится с помощью формул (61) и (66) - через ф-ии f(x) и делители m .

15. Композиционные ряды Галуа,

теория представлений и теория

мультиплетов.

8.1. Следуя своей тенденции мы в начале перечислим несколько самых основных для нас сведений из теории Галуа.

8.1.1. Чтобы алгебраическое полиномиальное уравнение

f(x)=0 (70)

решалось в радикалах необходимо и достаточно, чтобы его гр. Галуа была разрешимой.

8.1.2. Если группа G разрешима, то соответствующий ее композиционному ряду

G, G₁, G₂, ... , G_m-1 (71)

ряд факторгрупп

G/G₁, G₁/G₂, ... , G_m-2/G_m-1 , G_m-1 (72)

состоит из циклический групп, порядок которых

p, p₁, ... , p_n-1 - простые числа (или неприводимые в более широком контексте).

8.1.3. Обратно. Если (64) решается в радикалах, тогда существует композиционный ряд с рядом индексов.

-198-

(G:G₁), (G₁:G₂), ... , (G_m-2:G_m-1) , (73)

(G_m-1: Y) , состоящих из простых чисел ([5, Л-4], (7))

16. Теорема 11.

Т.к. уравнения деления круга

х^m-1=0 (74)

разрешимы (в уравнениях), то существует композиционный ряд с рядом индексов из простых чисел. Эта теорема -«составная» (см. две отдельных теоремы на стр. 113 и 121 ([10, Л-4], т.1.Чеботарев).

8.1. Теорема 12. (167 стр. [10, Л-4 ] )

Пусть

Х_m(х)=0 (75)

уравнение деления круга (с единственным решением в виде первообразного корня степени m из единицы). Группа Галуа этого уравнения есть абелева группа порядка -степени полинома Х_m(х)=0

8.2. Теорема 13.(66) (107 стр. [10, Л-4])

Существуют полиномы Х_m(х) с рациональными коэффициентами, корнями которых являются только первообразные m-ые корни из единицы.

8.3. Теорема 14.(64) (106 стр. [10, Л-4])

Уравнение (67) имеет корень в качестве первообразного.

(76)

Т. и т. тогда в дроби k/m число k взаимно просто с m, т.е. k/m (или: k и m не имеет общих множителей, кроме 1-цы)

8.4. Теорема 15. (утверждение на стр. 113,[10, Л-4]).

-199-

Группа поля m-ых корней из единицы , как прямое произведение циклических групп, есть абелева группа или группа поля из первообразного m-го корня из еди-ницы есть прямое произведение группы, изоморфных с группами полей корней из 1(единицы), степени которых являются степенями простых чисел.

8.5.

17. Связь схем приведения

представления к неприводимым

компонентам и процесса вычисления

членов композиционного ряда из

факторгрупп.

Теорема 16. (309 стр. [14, Л-4]).

Системы матриц А приводится с помощью базиса

А Р^-1АР (78)

т.и т.т. когда все матрицы системы А могут быть одновременно приведены к виду

(79)

8.6 Если фиксировать в случае представления кольца инвариантный подмодудь R и фактормодуль / и рассматривать их как модули представления, то получающиеся при этом представления задаются частями R и T матриц (72).

Далее. Если выбрать в максимальный инвариантный подмодуль _i-1, в котором вновь выберем

-200-

максимальный инвариантный подмодуль _i-1 и т.д., то получим композиционный ряд

= _m , _m-1 , ..., ₀ = (0) (80)

Тогда все матрицы представления в определенном базисе приобретают вид.

(81)

где диагональные клетки задают представления, которые отвечают композиционным факторам

_i/ _i-1 , (82)

которые далее неприводимы.

Этот процесс реализуем, если на каждом шагу соответствующий модуль представления (аддитивная группа представления) имеет собственный ненулевой подмодуль (подгруппу).

8.7. Поскольку (стр. 172 [13, Л-4]) векторы n- мерного векторного пространства образуют абелеву группу, умножением в которой является коммутативное сложение векторов, то постольку возникает прямые суммы соответственно подгрупп с линейными подпространствами, а автоморфизм -с - линейным отображением, что позволяет в случае прямой необходимости менять язык и терминологию при изложении сути дела.

8.8. Таким образом (стр. 173 [13, Л-4] ), если ^/ подпространство из , то пространство (mod ^/), полученное проецированием вдоль ^/, является точной аналогией факторгруппы. Т.е. можно говорить о

-201-

том, что композиционный ряд состоит из последовательности пространств, каждый член который есть линейное подпространство предыдущего члена (тоже подпространства) и имеет одним измерением меньше.

Последний член есть нульмерное «подпространство» 0 из нулевого вектора, отметим, что построение композиционного ряда в двух противоположных направлениях - возрастающем и убывающем - возможно благодаря коммутативности сложения векторов.

8.9.

Воспользовавшись синтетическим подходом к выше изложенным фактам на групповом и пространственных языках и теоремой об инвариантных множителях (стр. 300, 298-302 [14, Л-4]) мы завершим представление R→D

в более удобной и законченной формуле без правого ненулевого столбца в виде нормальной формы

, (83)

где E_i E_i+1 . Итак.

Теорема 17. (- об инвариантных множителях.)

Если - подмодуль линейных форм, то существует такой базис ( ₁, ... , _n ) в , что

_i= _iE_i

Причем, _k= ∑ _id_ik и (84)

-202-

(85)

Замечание. Если элементы не составляют линейной независимой системы, то возникает форма более общего вида.

, (86)

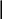г де r -ранг матрицы А. По-прежнему E _i E_i+1 . .