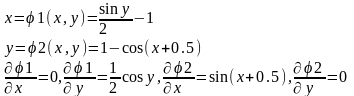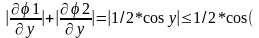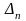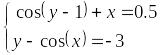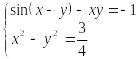Методичні вказівки
Приклад розв’язування одного варіанта.
1)
.
2)
.
1).
Перепишемо дану систему у вигляді
.
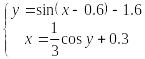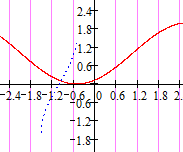
Відокремлення
коренів проводимо графічно (рис.1). Із
графіка бачимо, що система має один
розв’язок, розміщений в області
:
,
.
-
Рис.1
Переконаємося в тому, що метод ітерацій застосовний для уточнення розв’язку системи, для чого запишемо її у такому вигляді:
.
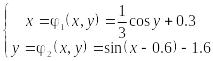Оскільки
,
,
,
,
то в області
маємо
,
.
Таким чином, умови збіжності виконуються.
Обчислення
проводимо за формулами
.
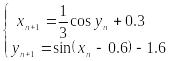Як
початкове наближення приймаємо
,
.
Таблиця 1
|
|
|
|
|
|
|
0 |
0.15 |
-2 |
-0.45 |
-0.4350 |
-0.4161 |
-0.1384 |
1 |
0.1616 |
-2.035 |
-0.4384 |
-0.4245 |
-0.4477 |
-0.1492 |
2 |
0.1508 |
-2.0245 |
-0.4492 |
-0.4342 |
-0.4382 |
-0.1461 |
3 |
0.1539 |
-2.0342 |
-0.4461 |
-0.4313 |
-0.4470 |
-0.1490 |
4 |
0.1510 |
-2.0313 |
-0.4490 |
0.4341 |
-0.4444 |
-0.1481 |
5 |
0.1519 |
-2.0341 |
-0.4481 |
-0.4333 |
-0.4469 |
-0.1490 |
6 |
0.1510 |
-2.0333 |
-0.4490 |
-0.4341 |
-0.4462 |
-0.1487 |
7 |
0.1513 |
-2.0341 |
-0.4487 |
-0.4340 |
-0.4469 |
-0.1490 |
8 |
0.1510 |
-2.0340 |
|
|
|
|
Відповідь:
,
.
2)
Відокремлення коренів проводимо графічно
(рис.2). Для побудови графіків функцій
складемо таблицю значень функцій
та
,
що входять до першого та другого рівняння
(табл.2).
Таблиця 2
|
-1.1 |
-1 |
-0.8 |
-0.6 |
-0.2 |
-0.4 |
0 |
0.2 |
0.4 |
0.5 |
|
1.21 |
1 |
0.64 |
0.36 |
0.04 |
0.16 |
0 |
0.04 |
0.16 |
0.25 |
|
0.97 |
0.8 |
0.51 |
0.29 |
0.032 |
0.13 |
0 |
0.032 |
0.13 |
0.2 |
|
0.03 |
0.2 |
0.49 |
0.71 |
0.97 |
0.87 |
1 |
0.97 |
0.87 |
0.8 |
|
-0.02 |
0.13 |
0.33 |
0.47 |
0.65 |
0.58 |
0.67 |
0.65 |
0.58 |
0.53 |
|
|
0.36 |
|
|
|
|
0.82 |
|
|
0.73 |
|
-1.32 |
-1.2 |
-0.96 |
-0.72 |
-0.24 |
-0.48 |
0 |
0.24 |
0.48 |
0.6 |
|
-0.92 |
-0.8 |
-0.56 |
-0.32 |
0.16 |
-0.08 |
0.4 |
0.64 |
0.88 |
1 |
|
-1.17 |
-0.93 |
-0.59 |
-0.33 |
0.16 |
-0.08 |
0.41 |
0.69 |
2.06 1.08 |
1.57 |
|
-1.03 |
-1.07 |
-1.01 |
-0.87 |
-0.56 |
-0.72 |
-0.41 |
-0.29 |
-1.26 -1.28 |
-0.57 |
0.14
Значення
для
можна брати виходячи із таких умов: із
першого рівняння
,
тобто
;
із другого рівняння
,
тобто
.
Таким чином,
.
-
Рис.2
Система
має два розв’язки. Уточнимо один із
них, що належить області
:
,
.
Маємо
.
,
.
Уточнення коренів проводимо методом Ньютона:
,
де
,
,
,
,
.
Всі обчислення виконуємо в таблиці 3.
Таблиця 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
0.4 |
0.128 |
0.55 |
0.9988 |
0.1198 |
-1.1584 |
-0.0208 |
2.6197 |
0.2701 |
0.10 |
0.75 |
0.8438 |
0.0208 |
-0.0282 |
0.64 |
-2.25 |
0.0440 |
0.017 |
|||
1 |
0.50 |
0.2 |
0.733 |
0.9869 |
-0.0131 |
-1.523 |
0.1615 |
3.2199 |
-0.0193 |
-0.0060 |
-0.733 |
0.8059 |
-0.1615 |
0.059 |
0.8 |
-2.199 |
0.0794 |
0.0247 |
|||
2 |
0.4940 |
0.1952 |
1.6963 |
0.9921 |
-0.0007 |
-1.4502 |
0.1251 |
2.9827 |
-0.0080 |
-0.0027 |
-0.7083 |
0.7525 |
-0.1251 |
-0.0523 |
0.7904 |
-2.1249 |
-0.0003 |
-0.0256 |
|||
3 |
0.4913 |
0.1931 |
1.7165 |
0.9894 |
-0.0002 |
-1.4904 |
0.1452 |
3.1673 |
-0.0003 |
-0.0001 |
-0.7339 |
0.8079 |
-0.1452 |
-0.1452 |
0.7861 |
-2.2017 |
0.0013 |
0.0004 |
|||
4 |
0.4912 |
|
|
|
|
|
|
|
|
|
-0.7335 |
|
|
|
|
|
|
|
|
|
Відповідь:
,
.
Приклад
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
варіант |
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
-1,2 |
< x < |
-0,6 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
< y < |
0,6 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
( |
-1,9 |
) = |
-0,99 |
<=1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1,3 |
) = |
0,4818 |
<1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
умови збіжності виконуються |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Початкове наближення приймаємо |
x0 = |
-0,6 |
|
|
|
|
|
|
|
|
|
|
|||||||
y0 = |
0,6 |
|
|
|
|
|
|
|
|
|
|
||||||||
xn |
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,6 |
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,7177 |
0,0050 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9975 |
0,0236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9882 |
0,1212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9395 |
0,1168 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9417 |
0,0951 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9525 |
0,0960 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9521 |
0,1007 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9498 |
0,1005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,9499 |
0,0994 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-0,950 |
0,099 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Із 2 рівняння |
-1,00 |
< x < |
1,00 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Система має два розв’язки. Уточнимо один з них |
|
|
|
|
|||||||||||||||
|
0 |
< x < |
0,6 |
|
|
|
|
|
|
|
|
|
|
||||||
|
0,6 |
< y < |
1,2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
xn |
yn |
F(x;y) |
G(x;y) |
F'x |
F'y |
G'x |
G'y |
|
|
|
|
|
|
||||||
0 |
0,6 |
0,3646 |
-0,6400 |
-0,6747 |
0,8253 |
0,0000 |
1,2000 |
-0,8096 |
|
|
|
|
|
||||||
1,1929 |
1,1333 |
-1,2614 |
1,7075 |
-2,1856 |
-0,6856 |
2,3858 |
2,2667 |
-3,3183 |
|
|
|
|
|
||||||
0,6841 |
0,9156 |
-0,2265 |
0,3063 |
-1,5289 |
-0,0289 |
1,3681 |
1,8313 |
-2,7603 |
|
|
|
|
|
||||||
0,5370 |
0,8582 |
-0,0209 |
0,0249 |
-1,3253 |
0,1747 |
1,0740 |
1,7165 |
-2,4625 |
|
|
|
|
|
||||||
0,5207 |
0,8539 |
-0,0002 |
0,0003 |
-1,3051 |
0,1949 |
1,0414 |
1,7078 |
-2,4318 |
|
|
|
|
|
||||||
0,5205 |
0,8539 |
0,0000 |
0,0000 |
-1,3048 |
0,1952 |
1,0410 |
1,7077 |
-2,4314 |
|
|
|
|
|
||||||
0,5205 |
0,8539 |
0,0000 |
0,0000 |
-1,3048 |
0,1952 |
1,0410 |
1,7077 |
-2,4314 |
|
|
|
|
|
||||||
|
|
|
|
|
-0,9658 |
-0,4318 |
1,1929 |
0,5333 |
|
1,6885 |
0,7224 |
-0,5089 |
-0,2177 |
|
0,4060 |
0,1584 |
-0,1471 |
-0,0574 |
|
0,0402 |
0,0106 |
-0,0163 |
-0,0043 |
|
0,0004 |
0,0002 |
-0,0002 |
-0,0001 |
|
0,0000 |
0,0000 |
0,0000 |
0,0000 |
|
0,0000 |
0,0000 |
0,0000 |
0,0000 |
|
Варіанти індивідуальних завдань:
1. |
1)
|
2)
|
2. |
1)
|
2)
|
3. |
1)
|
2)
|
4. |
1)
|
2)
|
5. |
1)
|
2)
|
6. |
1)
|
2)
|
7. |
1)
|
2)
|
8. |
1)
|
2)
|
9. |
1)
|
2)
|
10. |
1)
|
2)
|
11. |
1)
|
2)
|
12. |
1)
|
2)
|
13. |
1)
|
2)
|
14. |
1)
|
2)
|
15. |
1)
|
2)
|
16. |
1)
|
2)
|
17. |
1)
|
2)
|
18. |
1)
|
2)
|
19. |
1)
|
2)
|
20. |
1)
|
2)
|
21. |
1)
|
2)
|
22. |
1)
|
2)
|
23. |
1)
|
2)
|
24. |
1)
|
2)
|
25. |
1)
|
2)
|
26. |
1)
|
2)
|
27. |
1)
|
2)
|
28. |
1)
|
2)
|
29. |
1)
|
2)
|
30. |
1)
|
2)
|
