
- •Значуща цифра
- •Округлення чисел
- •Похибка суми
- •Похибка добутку
- •Частинний випадок: При множенні наближеного числа на точний множник відносна гранична похибка не змінюється, а абсолютна гранична похибка збільшується в разів.
- •Правило. Якщо всі співмножники мають m правильних десяткових знаків і кількість їх не більша 10, то кількість правильних знаків в добутку на одну або дві одиниці менше m .
- •Похибка частки
- •Кількість правильних знаків частки.
- •Відносна похибка степеня
- •Відносна похибка частки Теорема. Гранична відносна похибка кореня -го степеня в разів менша граничної відносної похибки підкореневого числа. ( ). Похибка різниці
- •Обчислення без точного врахування похибок
- •Пряма задача теорії похибок
- •Обернена задача теорії похибок
- •Метод меж
- •Методичні вказівки
- •Індивідуальні завдання
- •Лабораторна робота № 2.
- •Мета: Вивчити та набути практичні навички розв’язування нелінійних рівнянь з однією змінною наближеними методами. Завдання:
- •Теоретичні відомості
- •Індивідуальні завдання
- •Контрольні запитання
- •Мета: Вивчити та набути практичні навички розв’язування систем нелінійних рівнянь наближеними методами. Завдання:
- •Методичні вказівки
- •Контрольні запитання
- •Теоретичні відомості
- •Контрольні запитання
- •Лабораторна робота №5 Методи розв’язування задач про власні значення та власні вектори матриць
- •Теоретичні відомості та методичні рекомендації
- •Контрольні запитання
- •Індивідуальні завдання
- •Інтерполювання сплайнами
- •Мета: Вивчити методику та набути практичних навичок інтерполювання сплайнами таблично заданих функції.
- •Завдання: Побудувати кубічний сплайн таблично заданої функції у відповідності із індивідуальним завданням, наведеним у таблиці.
- •Теоретичні відомості
- •Індивідуальні завдання
- •Контрольні запитання
- •Теоретичні відомості
- •Варіанти завдань Чисельне диференціювання
- •Чисельне інтегрування
- •Результат розв’язання наведено в таблицях
- •Метод Рунге - Кутта
- •Індивідуальні завдання
- •Тема:Наближене розв’язування диференціального рівняння методом Адамса.
- •Лабораторна робота №13
- •Рівняння еліптичного типу.
- •Рівняння параболічного типу.
- •Лабораторна робота №15
Лабораторна робота № 2.
Тема: Розв’язування нелінійних рівнянь з однією змінною.
Мета: Вивчити та набути практичні навички розв’язування нелінійних рівнянь з однією змінною наближеними методами. Завдання:
1. Графічним методом та за допомогою ЕОМ відокремити корені рівняння (див. табл.1).
2.
Використовуючи метод простої ітерації
обчислити один корінь рівняння з точністю
![]() .
.
3. Розв’язати рівняння комбінованим методом хорд і дотичних.
Теоретичні відомості
Постановка задачі
Якщо функція
![]() визначена і неперервна на деякому
проміжку
визначена і неперервна на деякому
проміжку
![]() ,
то розв’язання рівняння
,
то розв’язання рівняння
![]() зводиться до відшукання множини значень
зводиться до відшукання множини значень
![]() ,
при яких це рівняння перетворюється у
тотожність.
,
при яких це рівняння перетворюється у
тотожність.
Знаходження наближених коренів рівняння складається із двох етапів:
– відокремлення коренів, тобто знаходження досить малих відрізків, на кожному з яких міститься один і тільки один корінь рівняння;
– уточнення кореня із наперед
заданою точністю
![]() .
.
Для відокремлення
коренів можемо використати
відому теорему: якщо неперервна функція
![]() на кінцях відрізку
на кінцях відрізку
![]() приймає значення протилежних знаків
(
приймає значення протилежних знаків
(![]() ),
то відрізок містить принаймні один
корінь рівняння
),
то відрізок містить принаймні один
корінь рівняння
![]() .
А якщо вдасться встановити монотонність
функції
на
,
то на цьому відрізку міститься ізольований
корінь.
.
А якщо вдасться встановити монотонність
функції
на
,
то на цьому відрізку міститься ізольований
корінь.
Якщо
![]() ,
то корінь рівняння
можна знайти як точку перетину графіків
функцій
,
то корінь рівняння
можна знайти як точку перетину графіків
функцій
![]() ,
,
![]() .
.
Наведемо, можливо не зовсім
коректний, але часто вживаний спосіб
відокремлення коренів рівняння
на відрізку
,
де
визначена, неперервна і
.
Точками
![]() (
(![]() ,
,
![]() ,
,
![]() )
розбиваємо відрізок
на
частин. Як тільки
)
розбиваємо відрізок
на
частин. Як тільки
![]() і функція
монотонна на відрізку
і функція
монотонна на відрізку
![]() ,
то вважатимемо, що на
міститься єдиний корінь. Зауважимо, що
при такому відокремленні коренів
необхідно вибирати досить малі значення
кроку
.
,
то вважатимемо, що на
міститься єдиний корінь. Зауважимо, що
при такому відокремленні коренів
необхідно вибирати досить малі значення
кроку
.
Метод хорд
Нехай
дано рівняння
![]() де функція
на відрізку
де функція
на відрізку
![]() має неперервні похідні першого і другого
порядків, які зберігають сталі знаки
на цьому відрізку, причому
має неперервні похідні першого і другого
порядків, які зберігають сталі знаки
на цьому відрізку, причому
![]() тобто корінь
тобто корінь
![]() рівняння відокремлений на
.
рівняння відокремлений на
.
Ідея
методу хорд в тому, що на досить малому
відрізку дуга кривої
![]() замінюється хордою і абсциса точки
перетину хорди з віссю
замінюється хордою і абсциса точки
перетину хорди з віссю
![]() є
наближеним значенням кореня.
є
наближеним значенням кореня.
Метод хорд можна записати так:
![]() ,
,
![]() де
де
![]() .
.
Метод Ньютона (дотичних)
Нехай рівняння
![]() на відрізку
на відрізку
![]() має ізольований корінь
,
тобто
а функції
,
має ізольований корінь
,
тобто
а функції
,
![]() неперервні і зберігають знаки на відрізку
.
неперервні і зберігають знаки на відрізку
.
Геометричний зміст методу:
дуга кривої
![]() замінюється дотичною до цієї кривої.
замінюється дотичною до цієї кривої.
Формула
![]() ,
визначає метод Ньютона.
,
визначає метод Ньютона.
Як початкове наближення у
методі Ньютона треба брати точку
![]() ,
в якій
,
в якій
![]() .
Як
.
Як
![]() прийнято брати відповідний кінець
відрізку
.
прийнято брати відповідний кінець
відрізку
.
Комбінований метод дотичних і хорд
Характерна особливість методів дотичних і хорд та, що послідовності їх наближень монотонні. Причому, якщо для даного рівняння послідовність наближень методу хорд монотонно спадна, то послідовність наближень методу дотичних – монотонно зростаюча, і навпаки. Одночасне застосування цих методів дає змогу наближатися до кореня рівняння з двох боків, дістаючи наближення з недостачею і надвишкою.
За
наведеними раніше умовами для одного
методу як початкове наближення вибирають
точку
![]() а в іншому точку
а в іншому точку
![]() Після застосовуння методів хорд та
дотичних дістають нові наближення
Після застосовуння методів хорд та
дотичних дістають нові наближення
![]() і початковий відрізок ізоляції кореня
відрізку
і початковий відрізок ізоляції кореня
відрізку
![]() звузився. Для знаходження нових наближень
застосовують метод дотичних і хорд уже
на відрізку
звузився. Для знаходження нових наближень
застосовують метод дотичних і хорд уже
на відрізку
![]() .
У результаті дістають нові наближення
.
У результаті дістають нові наближення
![]() відповідно, причому
відповідно, причому
![]() .
Такий процес продовжують доки довжина
відрізка
.
Такий процес продовжують доки довжина
відрізка
![]() не стане меншою або рівною величині
не стане меншою або рівною величині
![]() ,
де
-
наперед задана точність.
,
де
-
наперед задана точність.
Метод простої ітерації
Замінимо
рівняння
рівносильним рівнянням
![]() .
Нехай
.
Нехай
![]() -
корінь цього рівняння, а
-
корінь цього рівняння, а
![]() – одержане будь-яким способом початковим
наближенням до кореня
.
Підставляючи
у праву частину рівняння, одержимо деяке
число
– одержане будь-яким способом початковим
наближенням до кореня
.
Підставляючи
у праву частину рівняння, одержимо деяке
число
![]() .
Зробимо те ж саме з
,
одержимо
.
Зробимо те ж саме з
,
одержимо
![]() і так далі. Використовуючи крок за кроком
співвідношення
і так далі. Використовуючи крок за кроком
співвідношення
![]() для
для
![]() одержуємо числову послідовність
,
,…,
одержуємо числову послідовність
,
,…,
![]() ,….,
яку називають
ітераційною послідовністю,
може бути як збіжною,
так і розбіжною.
,….,
яку називають
ітераційною послідовністю,
може бути як збіжною,
так і розбіжною.
Теорема збіжності ітераційної послідовності. Нехай рівняння має єдиний корінь на відрізку і виконані умови:
визначена і диференційована на ;
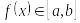 для всіх
для всіх
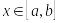 ;
;існує таке дійсне
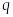 ,
що
,
що
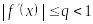 для всіх
для всіх
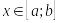 .
.
Тоді
ітераційна послідовність
,
збігається при будь-якому початковому
наближенні
![]() .
.
Перетворення рівняння до ітераційного вигляду
Рівняння
може бути приведено
до ітераційного вигляду різними
способами, проте необхідно зробити так,
щоб для функції
![]() виконувались умови теореми збіжності.
З цією метою рівняння
подамо у вигляді
виконувались умови теореми збіжності.
З цією метою рівняння
подамо у вигляді
![]() ,
,![]() де
стала
де
стала
![]() .
Тоді позначимо
.
Тоді позначимо
![]() Диференціюючи, отримуємо
Диференціюючи, отримуємо
![]() .
Для виконання умови 3 теореми збіжності
потрібно
.
Для виконання умови 3 теореми збіжності
потрібно
![]() .
А для цього досить підібрати сталу
так, щоб для фіксованого
виконувалося
.
А для цього досить підібрати сталу
так, щоб для фіксованого
виконувалося
![]() Підставимо це значення
у рівняння
і отримуємо схему збіжного ітераційного
процесу.
Підставимо це значення
у рівняння
і отримуємо схему збіжного ітераційного
процесу.
Приклад
Варіант |
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xЄ [ |
0,2 |
0,6 |
] |
x наб = |
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
0,9345 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x=x0= |
0,4 |
|
|
|
|
|
|
|
|
x1=f(x0)= |
0,4169 |
|
|
|
|
|
|
|
|
x2=f(x1)= |
0,4096 |
|
|
|
|
|
|
|
|
x3=f(x2)= |
0,4127 |
|
|
|
|
|
|
|
|
x4=f(x3)= |
0,4114 |
|
|
|
|
|
|
|
|
x5=f(x4)= |
0,4120 |
|
|
|
|
|
|
|
|
|
0,4117 |
|
|
|
|
|
|
|
|
x ~ |
0 |
|
|
|
|
|
|
|
|
3) Метод хорд |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
|
|
|
|||
Ф ормула , визначає метод Ньютона |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
a |
b |
f(a) |
f(b) |
f'(b) |
|
|
|
|
|
0,2 |
0,6 |
-0,36577 |
0,263796 |
1,032645 |
|
|
|
|
|
0,432395 |
0,344543 |
0,031125 |
-0,10627 |
1,079112 |
|
|
|
|
|
0,412494 |
0,443027 |
0,001063 |
0,04695 |
1,062542 |
|
|
|
|
|
0,411787 |
0,398840 |
-1,6E-05 |
-0,01991 |
1,070297 |
|
|
|
|
|
0,411797 |
0,412832 |
3,47E-13 |
0,001579 |
1,067889 |
|
|
|
|
|
0,411797 |
0,411354 |
0 |
-0,00068 |
1,068146 |
|
|
|
|
|
0,412 |
0,412 |
0 |
6,15E-08 |
1,068069 |
|
|
|
|
|

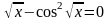
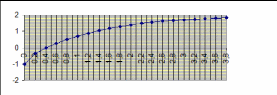


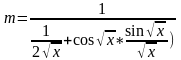
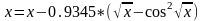
 ,412
,412

 етод
дотичних(Ньютона)
етод
дотичних(Ньютона)