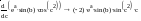Обернена задача теорії похибок

Визначити, якими повинні бути абсолютні похибки аргументів функції , щоб абсолютна похибка функції не перевищувала заданої величини?

Цю задачу можна розв’язати, користуючись принципом рівних впливів.

Згідно з цим принципом припускають, що всі частинні диференціали однаково впливають на утворення загальної абсолютної похибки функції .

Нехай величина граничної абсолютної похибки задана. Тоді .

Припускаючи, що всі доданки рівні між собою, будемо мати :

.

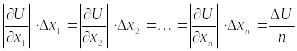Отже, , .

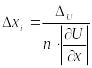Інколи припускають, що гранична абсолютна похибка всіх однакова, тобто

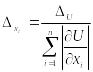, де .

Припускаючи, що точність усіх вимірювань однакова, отримаємо формулу

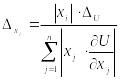, де .

Метод меж

У певних випадках потрібно мати точні границі для шуканого значення функції, якщо відомі границі зміни її аргументів.

Для цього користуються способом подвійних обчислень, який ще називають методом меж. Нехай – неперервно-диференційовна функція, монотонна по кожному аргументу у розглядуваній області зміни аргументів.

Припустимо, що похідні , зберігають постійний знак у цій області.

Покладемо , .

Позначимо: ; .

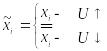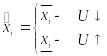Тоді очевидно, що , де , .

Зауваження. Змінні і результати дії над ними можна округлювати лише в сторону зменшення , а і результат дії над ними лише в сторону збільшення .

Методичні вказівки

Приклад 1. Знайти суму наближених чисел : 0,348; 0,1834; 345,4; 235,2; 11,75; 9,27; 0,0849; 0,0214; 0,000354.

Розв’язування.

1) Виділимо числа абсолютної точності. Абсолютна похибка їх може бути 0,05 (оскільки маємо числа 345,4; 235,2).

2) Округлюємо всі останні числа до сотих.

3) 345,4 + 235,2 + 11,75 + 9,27 + 0,35 + 0,18 + 0,08 + 0,02 + 0,00 = 602,25

4) Одержаний результат округлюємо до десятих : .

Повна похибка результату складається з трьох доданків :

1) з суми граничних похибок вхідних даних

2) абсолютної величини суми похибок (з врахуванням знаків округлення доданків):

3) залишкова похибка округлення результату: .

.

Приклад 2. Визначити добуток наближених чисел і і число правильних знаків у ньому, якщо всі записані цифри співмножників правильні.

Розв’язування.

Граничні похибки співмножників: ; .

Відносна похибка добутку : . .

Правильними є лише перші дві цифри.

Отже, .

Приклад 3. Знайти кількість правильних знаків частки .

Розв’язування.

.

Знайдемо граничну абсолютну похибку : .

Правильних знаків буде два, тобто ми можемо зберегти один знак . .

Приклад 4. Знайти граничні абсолютну та відносну похибки об’єму кулі , якщо м, .

Розв’язування.

Розглянемо і як змінні величини.

Обчислимо частинні похідні : ; .

Гранична абсолютна похибка обчислення об’єму

. .

Гранична відносна похибка об’єму , .

Приклад 5. Радіус основи циліндра , висота . З якими абсолютними похибками треба визначити і , щоб об’єм циліндра отримати із точністю до

Розв’язування.

, . Покладемо , .

; ; ;

; ; .

Приклад 6. Алюмінієвий циліндр з діаметром основи , висотою , має масу .Визначити густину алюмінію і оцінити її граничну абсолютну похибку.

Розв’язування.

, ,

Функція - зростаюча по аргументу і спадна по аргументам і :

; ; ; ;

(з недостачею);

(з надвишкою).

_{Візьмемо середнє арифметичне} . Після округлення маємо

_{Приклад 7.}

Варіант	26
			a	b	c	e
			-2,301	1,72	-0,002	2,7183
Завдання:
1.      Виконати зазначені дії з точним врахуванням правильних цифр.
2.      Обчислити значення та похибку виразу методом меж.
3.      Розв’язати пряму задачу теорії похибок.
4.      Розв’язати обернену задачу теорії похибок.
Завдання 1
		Z=				=		0,0990
Завдання 2
-2,3015	≤ a ≤	-2,3006
1,715	≤ b ≤	1,724
-0,0025	≤ c ≤	-0,0016
2,71825	≤ e ≤	2,71834
Нижню і верхню межу числа підставляємо таку, щоб значення було відповідно найменшим та найбільшим.
Zв =						0,0992
Zн =						0,0991
Zсер=			0,099113
Похибка:	0,00004
Відповідь:	0,099	±	0,00004
Завдання 3
Z=

	a =	-2,301	±		0,0005
	b =	1,72	±		0,005
	c =	-0,002	±		0,0005
	e =	2,7183	±		0,00005
Z'a = (b(ln(a)+3b)-(ab-4c)/a)/(ln(a)+3b)^2 =					0,09904			Z'e =	0,0000
Z'b = (a(ln(a)+3b)-3(ab-4c))/(ln(a)+3b)^2 =					-0,0149
=					1,58471E-09
ΔZ =	0,000124
Z =	0,099	±	0,0001
Гранична відносна похибка	δε=	0,001252
Завдання 4
ΔZ =	0,1
Δa <	-0,0109
Δb <	0,0145
Δc <	-12,5000
Δe<	0,0092