
- •Значуща цифра
- •Округлення чисел
- •Похибка суми
- •Похибка добутку
- •Частинний випадок: При множенні наближеного числа на точний множник відносна гранична похибка не змінюється, а абсолютна гранична похибка збільшується в разів.
- •Правило. Якщо всі співмножники мають m правильних десяткових знаків і кількість їх не більша 10, то кількість правильних знаків в добутку на одну або дві одиниці менше m .
- •Похибка частки
- •Кількість правильних знаків частки.
- •Відносна похибка степеня
- •Відносна похибка частки Теорема. Гранична відносна похибка кореня -го степеня в разів менша граничної відносної похибки підкореневого числа. ( ). Похибка різниці
- •Обчислення без точного врахування похибок
- •Пряма задача теорії похибок
- •Обернена задача теорії похибок
- •Метод меж
- •Методичні вказівки
- •Індивідуальні завдання
- •Лабораторна робота № 2.
- •Мета: Вивчити та набути практичні навички розв’язування нелінійних рівнянь з однією змінною наближеними методами. Завдання:
- •Теоретичні відомості
- •Індивідуальні завдання
- •Контрольні запитання
- •Мета: Вивчити та набути практичні навички розв’язування систем нелінійних рівнянь наближеними методами. Завдання:
- •Методичні вказівки
- •Контрольні запитання
- •Теоретичні відомості
- •Контрольні запитання
- •Лабораторна робота №5 Методи розв’язування задач про власні значення та власні вектори матриць
- •Теоретичні відомості та методичні рекомендації
- •Контрольні запитання
- •Індивідуальні завдання
- •Інтерполювання сплайнами
- •Мета: Вивчити методику та набути практичних навичок інтерполювання сплайнами таблично заданих функції.
- •Завдання: Побудувати кубічний сплайн таблично заданої функції у відповідності із індивідуальним завданням, наведеним у таблиці.
- •Теоретичні відомості
- •Індивідуальні завдання
- •Контрольні запитання
- •Теоретичні відомості
- •Варіанти завдань Чисельне диференціювання
- •Чисельне інтегрування
- •Результат розв’язання наведено в таблицях
- •Метод Рунге - Кутта
- •Індивідуальні завдання
- •Тема:Наближене розв’язування диференціального рівняння методом Адамса.
- •Лабораторна робота №13
- •Рівняння еліптичного типу.
- •Рівняння параболічного типу.
- •Лабораторна робота №15
Рівняння параболічного типу.
Мета: навчитися розв’язувати задачі в частинних похідних параболічного типу.
Завдання
Використовуючи метод сіток, скласти
розв’язок змішаної задачі для
диференціального рівняння параболічного
типу
 (рівняння теплопровідності) при заданих
початкових умовах
(рівняння теплопровідності) при заданих
початкових умовах
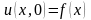 ,
,
 ,
,
 ,
де
,
де
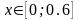 .
Розв’язування виконати при
,
для
.
Розв’язування виконати при
,
для
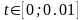 з чотирма десятковими цифрами, вважаючи
з чотирма десятковими цифрами, вважаючи
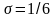 .
.
Приклад
розв’язання задачі:
 ,
,
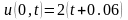 ,
,
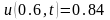 .
.
Параболічне
рівняння розв’язується методом сіток
поступовим переходом від значень функції
 до значень
до значень
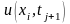 ;
причому
;
причому
 ,
де
,
де
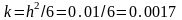 .
.
Обчислення виконують за формулою
 (
(
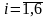 ;
;
 ).
).
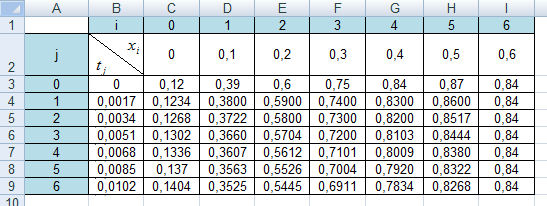
Усі розрахунки здійснені засобами MS Excel і наведені в таблиці:
Варіанти завдань:
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
, |
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
. |
16. |
|
, |
. |
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
|
21. |
|
|
|
22. |
|
|
|
23. |
|
|
|
24. |
|
|
|
25. |
|
|
|
26. |
|
|
|
27. |
|
|
|
28. |
|
|
|
29. |
|
|
|
30. |
|
, |
|
Контрольні запитання:
1. Рівняння теплопровідності.
2. Розрахункові формули.
Лабораторна робота №15
Тема: Наближені методи розв’язування задач в частинних похідних.
Рівняння гіперболічного типу.
Мета: навчитися розв’язувати задачі в частинних похідних гіперболічного типу.
Завдання:Використовуючи
метод сіток, скласти розв’язок змішаної
задачі для рівняння коливання струни
 з початковими умовами
,
з початковими умовами
,
 (
(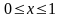 )
і крайовими умовами
,
)
і крайовими умовами
,
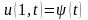 .
Розв’язування виконати з кроком
,
визначаючи значення функції
.
Розв’язування виконати з кроком
,
визначаючи значення функції
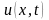 з чотирма десятковими знаками, причому
з чотирма десятковими знаками, причому
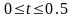 .
.
Приклад
розв’язання задачі:
 ,
,
 ,
,
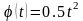 ,
,
 .
.
Для
розв’язування скористаємося
співвідношенням
 ,
де
,
де
 ;
;
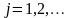 .
.
При
цьому
 ,
а для визначення
,
а для визначення
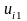 можна використати один із можливих
прийомів, наприклад,
можна використати один із можливих
прийомів, наприклад,
 ,
причому
,
причому
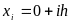 ,
(
,
( ),
),
 ,
,
 ,
(
,
( ).
Зокрема,
).
Зокрема,
 ;
;
 .
.
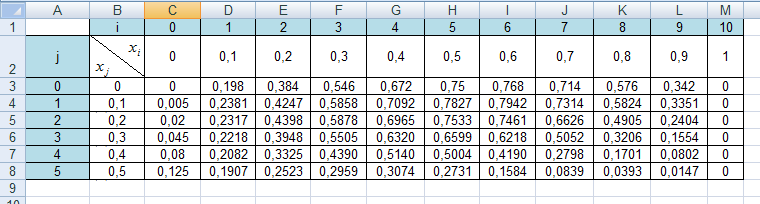
Розв’язування по наведеним формулам зручно виконувати в таблиці, яка і є розв’язанням даної задачі.
Порядок заповнення таблиці:
1.
Обчислюємо
 при
при
 і записуємо їх до першого рядка (він
відповідає значенню
і записуємо їх до першого рядка (він
відповідає значенню
 ).
).
2.
Обчислюємо значення
 при
при
 і записуємо їх до першого стовпця таблиці
(він відповідає значенню
і записуємо їх до першого стовпця таблиці
(він відповідає значенню
 ).
).
3.
Заносимо значення
 до останнього стовпчика таблиці (він
відповідає значенню
до останнього стовпчика таблиці (він
відповідає значенню
 ).
).
4.
Обчислюємо значення
 за формулою
за формулою
 ,
де
,
де
 та
та
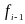 беруться із першого рядка таблиці, а
беруться із першого рядка таблиці, а
 ,
(
,
(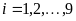 ),
),
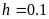 .
Результати записуємо до другого рядка
таблиці.
.
Результати записуємо до другого рядка
таблиці.
5.
Обчислюємо значення
 в наступних рядках за формулою
в наступних рядках за формулою
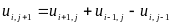 ,
де значення
,
де значення
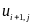 ,
,
 ,
,
 беруться із двох попередніх рядків
таблиці.
беруться із двох попередніх рядків
таблиці.
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
0.0 |
0 |
0.198 |
0.384 |
0.546 |
0.672 |
0.750 |
0.768 |
0.714 |
0.576 |
0.342 |
0 |
0.1 |
0.005 |
0.2381 |
0.4247 |
0.5858 |
0.7092 |
0.7827 |
0.7942 |
0.7314 |
0.5824 |
0.3351 |
0 |
0.2 |
0.02 |
0.2317 |
0.4398 |
0.5878 |
0.6965 |
0.7533 |
0.7461 |
0.6626 |
0.4905 |
0.2404 |
0 |
0.3 |
0.045 |
0.2218 |
0.3948 |
0.5505 |
0.6320 |
0.6599 |
0.6218 |
0.5052 |
0.3206 |
0.1554 |
0 |
0.4 |
0.08 |
0.2082 |
0.3325 |
0.4390 |
0.5140 |
0.5004 |
0.4190 |
0.2798 |
0.1701 |
0.0802 |
0 |
0.5 |
0.125 |
0.1907 |
0.2523 |
0.2959 |
0.3074 |
0.2731 |
0.1584 |
0.0839 |
0.0393 |
0,0147 |
0 |
Даний
приклад зручно розв’язувати засобами
MS
Excel.
Варіанти завдань:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
,
,
|
Контрольні запитання:
1. Коливання струни.
2. Що означають крайові умови.

 ,
, ,
, .
. ,
, ,
, .
.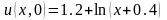 ,
, ,
, .
. ,
,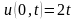 ,
, .
. ,
,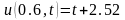 .
.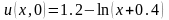 ,
,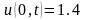 ,
, .
. ,
,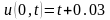 ,
, .
.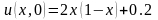 ,
, ,
, .
. ,
, ,
, .
. ,
,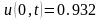 ,
, .
. ,
,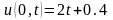 ,
,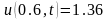 .
. ,
, ,
,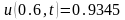 .
. ,
, ,
, .
. ,
, ,
, .
.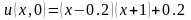
 ,
, ,
, ,
, ,
,
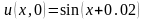 ,
, ,
, .
. ,
,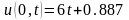 ,
,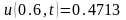 .
. ,
,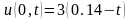 ,
, .
. ,
, ,
, .
. ,
, ,
, .
. ,
,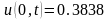 ,
,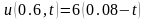
 ,
, ,
,
 ,
, ,
, .
. ,
, ,
,
 ,
, ,
, .
. ,
, ,
,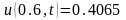 .
. ,
,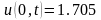 ,
,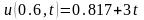
 ,
, .
.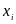

 ,
,
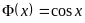 ,
,
 ,
,
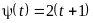 .
.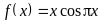 ,
,
 ,
,
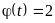 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
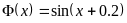 ,
,
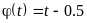 ,
,
 .
. ,
,
 ,
,
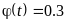 ,
,
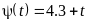 .
. ,
,
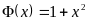 ,
,
,
,
 .
. ,
,
 ,
,
 ,
.
,
. ,
,
 ,
,
.
,
,
. ,
,
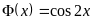 ,
,
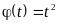 ,
,
 .
.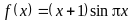 ,
,
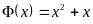 ,
,
,
,
 .
.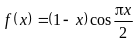 ,
,
 ,
,
 ,
.
,
.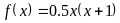 ,
,
 ,
,
 ,
,
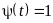 .
.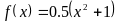 ,
,
 ,
,
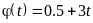 ,
.
,
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
,
,
 .
.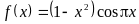 ,
,
 ,
,
 ,
.
,
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
,
,
 .
.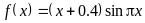 ,
,
,
.
,
,
,
. ,
,
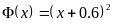 ,
,
.
,
,
. ,
,
 ,
,
,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
,
,
 .
.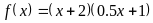 ,
,
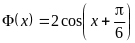 ,
,
,
,
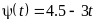 .
.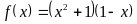 ,
,
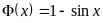 ,
,
.
,
,
.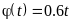 ,
,
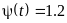 .
.