Теоретичні відомості
Чисельне диференціювання функцій
Після диференціювання інтерполяційного многочлена Ньютона
|
(1) |
,де
,
,,
дістанемо
|
(2) |
|
,
|
(3) |
.Якщо похідні обчислюють за формулами (2),(3) в точці , то за точку вибирають найближче табличне значення аргументу, яке менше за .
Формули
чисельного диференціювання (2),(3) значно
спрощуються, якщо значення похідних
обчислювати у вузлах інтерполювання.
Оскільки табличне значення можна взяти
за
,
то, поклавши у формулах (2),(3)
,
дістанемо
|
(4) |
|
(5) |
Приклад
1. У точці
знайти першу і другу похідні від функції
,
заданої таблицею
-
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,00000
0,90909
0,83333
0,76923
0,71429
0,66667
0,62500
0,58824
Побудуємо таблицю скінчених різниць
|
|
|
|
|
|
|
|
|
1 |
1,00000 |
|
|
|
|
|
|
|
|
|
-0,09091 |
|
|
|
|
|
|
1,1 |
0,90909 |
|
0,01515 |
|
|
|
|
|
|
|
-0,07576 |
|
-0,00349 |
|
|
|
|
1,2 |
0,83333 |
|
0,01166 |
|
0,00099 |
|
|
|
|
|
-0,06410 |
|
-0,00250 |
|
-0,00033 |
|
|
1,3 |
0,76923 |
|
0,00916 |
|
0,00066 |
|
0,00014 |
|
|
|
-0,05496 |
|
-0,00184 |
|
-0,00019 |
|
-0,00009 |
1,4 |
0,71429 |
|
0,00732 |
|
0,00047 |
|
0,00005 |
|
|
|
-0,04762 |
|
-0,00137 |
|
-0,00014 |
|
|
1,5 |
0,66667 |
|
0,00595 |
|
0,00033 |
|
|
|
|
|
-0,04167 |
|
-0,00104 |
|
|
|
|
1,6 |
0,62500 |
|
0,00491 |
|
|
|
|
|
|
|
-0,03676 |
|
|
|
|
|
|
1,7 |
0,58824 |
|
|
|
|
|
|
|
Оскільки
п’яті різниці практично сталі, то
покладемо
.
Точка
розміщена на початку таблиці, тому першу
і другу похідні обчислюватимемо за
формулами (4),(5). У цьому разі
;
;
;
;
;
;
.
Виконавши обчислення, знайдемо
.
.
Точні
значення похідних:
,
.
Приклад
2. Знайти для
=0,423
першу та другу похідні функції
,
заданої таблицею
-
0,4
0,5
0,6
0,7
0,8
0,9
2,8918247
3,1487213
3,4221188
3,7137527
4,0255409
4,3596031
Обчислення вести, враховуючи різниці до 5-го порядку включно.
Щоб
розв’язати задачу, записуємо, починаючи
із значення
частину даної таблиці і обчислюємо
потрібні нам різниці
|
|
|
|
|
|
|
0,4 |
2,8918247 |
|
|
|
|
|
|
|
0,2568966 |
|
|
|
|
0,5 |
3,1487213 |
|
0,0165009 |
|
|
|
|
|
0,2733975 |
|
0,0017355 |
|
|
0,6 |
3,4221188 |
|
0,0182364 |
|
0,0001824 |
|
|
|
0,2916339 |
|
0,0019179 |
|
0,0000194 |
0,7 |
3,7137527 |
|
0,0201543 |
|
0,0002018 |
|
|
|
0,3117882 |
|
0,0021197 |
|
|
0,8 |
4,0255409 |
|
0,0222740 |
|
|
|
|
|
0,3340622 |
|
|
|
|
0,9 |
4,3596031 |
|
|
|
|
|
У
даному прикладі маємо:
;
;
,
;
.
Підставляємо
отримані дані у формули (2),(3) і знаходимо
;
.
Чисельне інтегрування функцій
Формула
трапецій
.
Похибка
формули трапецій
,
.
Формула
Сімпсона
.
П
охибка
формули Сімпсона
,
,
.
Приклад ; a = 0, b = 1, N = 10.
Розв’язок отримано засобами MS Excel і наведено в таблицях
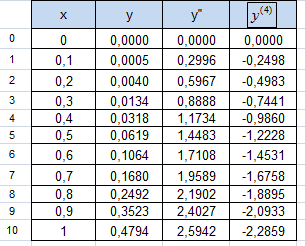
Формула трапецій
Похибка
формули трапецій
,
.
Формула Сімпсона
Похибка
формули Сімпсона
,
,
