Інтерполювання сплайнами
Мета: Вивчити методику та набути практичних навичок інтерполювання сплайнами таблично заданих функції.
Завдання: Побудувати кубічний сплайн таблично заданої функції у відповідності із індивідуальним завданням, наведеним у таблиці.
Теоретичні відомості
Наведемо спосіб побудови кубічних сплайнів.
Нехай
інтерпольована функція
задана своїми значеннями
в точках
(
).
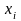Довжину відрізка
позначимо
.
Будемо шукати кубічний сплайн на кожному
із частинних відрізків
у вигляді
|
(1) |
,
де
,
,
,
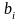– невідомі коефіцієнти.
Для
відрізків коефіцієнтів буде
.
Будемо
вимагати збігання значень
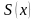у вузлах з табличними значеннями функції
:
|
(2) |
|
(3) |
,
.
Кількість
цих рівнянь (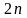
)
вдвічі менше кількості невідомих
коефіцієнтів; щоб отримати додаткові
умови, вимагатимемо також неперервності
і
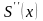у всіх точках, включаючи вузли. Для цього
треба прирівняти ліві і праві похідні
,
,
,
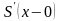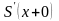у внутрішніх вузлах
.
Похідні:
,
.
Для
першої похідної маємо
,
,
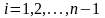(для
перш за все потрібно у виразі
замінити
на
).
Аналогічно для другої похідної:
,
,
.
Прирівнюючи ліві і праві похідні, отримуємо
|
(4) |
|
(5) |
,
,
.
Ці
рівняння дають ще
умов. Не вистачає ще дві умови. Як правило
їх приймають у вигляді вимоги до поведінки
сплайна у граничних точках
і
.
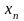Якщо
вимагати нульової кривини сплайна на
кінцях (тобто рівності нулю другої
похідної (
,
)),
то отримаємо
|
(6) |
,
.Перепишемо тепер всі рівняння (3)-(6), виключаючи невідомих :
|
|
|
(7) |
|
|
, |
|
. |
|
,
,
,
,
,
,
Система
(7) складається з
рівнянь. Розв’язуючи її, отримаємо
значення невідомих
,
,
(відомо, що
),
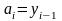що визначають сукупність усіх формул
для шуканого інтерполяційного сплайна
|
(8) |
,
.
Приклад.
Побудувати кубічний сплайн
,
якщо задано значення функції
,
:
|
|
,
,
,
,
,
.
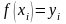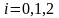На
кінцях відрізка
задані граничні умови
,
.
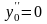Розв’язання.
Скористаємося розрахунковими формулами (7). Маємо:
1)
при
:
,
,
;
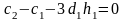2)
при
тільки:
,
додатково
,
.
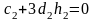Розв’язуючи
отриману систему 5 рівнянь з 5 невідомими
,
,
,
,
,
,
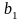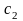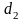знаходимо коефіцієнти сплайнів для
кожного із 2 відрізків.
Нагадаємо,
що
,
,
,
.
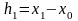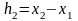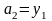Отож,
маємо
,
,
,
.
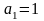Підставляємо
відомі величини
та значення
,
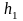отримуємо
,
,
,
,
,
.
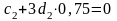Звідси маємо
,
,
,
,
,
.
Запишемо у вигляді таблиці
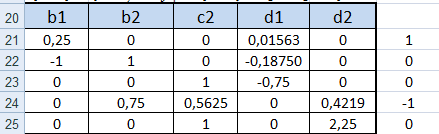
Найпростіший метод розв’язання системи засобами MS Excel – це матричний метод (знаходження оберненої матриці).
Після розв’язування цієї системи рівнянь маємо:
,
,
,
,
,
,
,
.
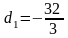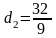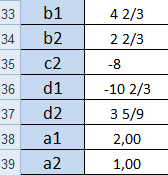
Таким чином, шуканий сплайн має вигляд
.
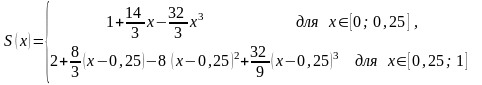Виконаємо перевірку правильності побудованого кубічного сплайна.
1.
;
;
.
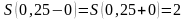2.
;
.
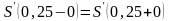3.
;
.
Індивідуальні завдання
-
№
№
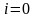
1
1
1,2
1,5
2
1
2
5
-1
2
1
-2
1
0
3
0
0,1
0,5
4
0,5
1
3
2
1
2
-1
0
2
5
0,2
0,25
0,5
6
0
1
4
0
1,5
2
1
4
2
7
0,1
0,3
0,7
8
0,2
0,5
2
0,5
1
0,2
0
4
1
9
1
1,5
1,75
10
0,3
0,5
1
0
1,3
2
-2
0
1
11
0,2
0,5
0,6
12
0
2
6
0,5
1
0,4
2
-2
1
13
0
0,5
0,6
14
0,2
0,3
0,8
2
1
1,5
2
1
3
15
0,3
0,4
0,7
16
0,1
0,5
1
0
1,5
2
0
3
2
17
0,1
0,25
0,6
18
1
1,4
1,5
0,1
0,6
1
1
-1
3
19
0
1
4
20
0
4
6
1
3
2
2
-1
2
21
0,2
0,5
1
22
0
0,7
1
0,1
0,35
0,6
0,25
1,2
1,4
23
1,2
1,4
2
24
0,5
0,65
1
0
0,5
1,2
0,75
0,5
0,1
25
0,3
0,5
1
26
0
0,75
1
-0,2
0,5
1,25
0,1
-0,2
0,4
27
0,1
0,2
0,5
28
0,4
0,5
0,7
-0,25
0,25
0,75
0,3
0,7
1
29
0
0,2
0,7
30
0,5
0,6
0,9
-1
1,2
0,5
0,25
0,75
0,5
31
0,2
0,8
1
32
0,3
0,4
1
0
0,6
0,4
0,5
0,25
0,5
33
0,3
0,4
1
34
0,2
0,3
1
-1
0
1,5
0
1
2
35
0,1
0,2
0,5
36
0,1
0,25
0,75
0,5
0,75
1,25
0
1
2
37
0,15
0,25
0,5
38
0,25
0,5
1
0,1
0,5
1
-1
1
3
39
0
0,15
0,5
40
0,1
2
4
0,5
1
2
0,5
1
2
41
0,2
0,25
5
42
0,1
0,2
0,4
0,1
0,2
0,3
0,2
0,25
5
43
0
0,35
0,5
44
0,1
0,6
1
0,5
0,75
1
1
0
1,5
45
0,1
0,15
0,45
46
0,25
0,75
1
0,5
0,6
1
0
0,5
1
47
0,6
0,7
1
48
0
0,2
0,9
0
1
2
2,5
1
0,5
49
0,15
0,3
0,5
50
0,1
0,8
1
0,25
0,5
1
0,8
1
1,5