^{Лабораторна робота № 1}

Тема:Елементи теорії похибок

Мета: Ознайомити з елементами теорії похибок. Набуття навичок обчислення значень функції із точним врахуванням похибок.

Завдання:

1. Виконати зазначені дії з точним врахуванням правильних цифр.

2. Обчислити значення та похибку виразу методом меж.

3. Розв’язати пряму задачу теорії похибок.

4. Розв’язати обернену задачу теорії похибок.

Теоретичні відомості

Абсолютна і відносна похибка

Наближеним числом називається число, що незначно відрізняється від точного числа і яке заміняє його в обчисленнях.

Різниця між точним числом та його наближеним числом називається похибкою. Абсолютна величина різниці і називається абсолютною похибкою або .

Під граничною абсолютною похибкою наближеного числа розуміють всяке число, не менше абсолютної похибки цього числа.

Відносною похибкою наближеного числа називається відношення абсолютної похибки цього числа до модуля відповідного точного числа . .

Граничною відносною похибкою наближеного числа називають всяке число, не менше відносної похибки цього числа. .

Значуща цифра

Будь-яке додатне число можна подати як:

.

Всі десяткові знаки , що зберігаються в написанні, називаються значущими цифрами наближеного числа.

Значущою цифрою наближеного числа називається всяка цифра в його десятковому поданні, відмінна від нуля і нуль, якщо він знаходиться між значущими цифрами.

Кажуть, що перших значущих цифр наближеного числа є правильними, якщо абсолютна похибка цього числа не перевищує половини одиниці розряду, що виражається -тою значущою цифрою, рахуючи зліва направо.

Округлення чисел

Округлення числа – це заміна його числом із меншою кількістю правильних цифр.

Правило округлення. Щоб округлити число до значущих цифр, відкидають усі наступні значущі цифри. При цьому, якщо:

– перша з відкинутих цифр менша 5, то остання залишена цифра залишається тією самою;

– перша з відкинутих цифр більша або рівна 5, то до останньої значущої цифри додається 1.

Похибка суми

Теорема. Абсолютна похибка алгебраїчної суми кількох наближених чисел не перевищує суми абсолютних похибок цих чисел: .

Наслідок 1: Як граничну абсолютну похибку алгебраїчної суми можна прийняти суму граничних абсолютних похибок доданків:

Наслідок 2. Гранична абсолютна похибка суми не може бути меншою граничної абсолютної похибки найменш точного з доданків.

Правило. Щоб додати числа різної абсолютної точності потрібно:

1. виділити числа, десятковий запис яких обривається раніше інших; залишити їх без зміни;

2. інші числа округлити за зразком виділених, зберігаючи один або два запасних десяткових знаків;

3. провести додавання чисел, враховуючи всі збережені знаки;

4. одержаний результат округлити на один розряд.

Похибка добутку

Теорема. Відносна похибка добутку кількох наближених чисел, відмінних від нуля, не перевищує суми відносних похибок цих чисел: .

Наслідок 1: Гранична відносна похибка добутку рівна сумі граничних відносних похибок співмножників:

Наслідок 2: Якщо всі співмножники добутку достатньо точні за винятком одного, то гранична відносна похибка буде співпадати з граничною відносною похибкою найменш точного співмножника.

Знаючи граничну відносну похибку добутку можна визначити абсолютну граничну похибку

Частинний випадок: При множенні наближеного числа на точний множник відносна гранична похибка не змінюється, а абсолютна гранична похибка збільшується в разів.

Нехай , де – наближене значення числа, – точний множник, тоді .

Правило. Щоб знайти добуток з кількох наближених чисел із різною кількістю правильних значущих цифр, досить:

1. округлити їх так, щоб кожне з них містило на одну або на дві значущі цифри більше, ніж кількість правильних цифр в найменш точному із співмножників;

2. в результаті множення зберігти стільки значущих цифр, скільки правильних цифр в найменш точному співмножнику або утримати ще одну запасну цифру.

Правило. Якщо всі співмножники мають m правильних десяткових знаків і кількість їх не більша 10, то кількість правильних знаків в добутку на одну або дві одиниці менше m .

Зауваження. Якщо співмножники мають різну точність, то під m слід розуміти кількість знаків в найменш точному із співмножників.

Похибка частки

Теорема. Відносна похибка частки не перевищує суми відносних похибок діленого і дільника.

Наслідок. Якщо , то гранична відносна похибка .

Кількість правильних знаків частки.

Нехай ділене і дільник мають хоча б m правильних цифр. Якщо і – їх перші значущі цифри, то як граничну відносну похибку можна прийняти величину

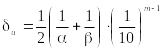
Правило:

1) якщо і , то частка має щонайменше правильних цифр;

2) якщо або , то частка має правильних знаки.