
- •1. Невизначений, визначений та невласний інтеграли
- •3. Ряди
- •Список літератури
- •5. Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.
- •Види диференціальних рівнянь першого порядку:
- •6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку
- •Рівняння вигляду .
- •7. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами
- •8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною
- •9. Метод варіації довільних сталих.
- •Література
- •Тема 3. Ряди
- •Гранична ознака порівняння
- •Знакопочережні ряди
- •Ознака Лейбніца
- •Розвинення елементарних функцій у ряди
1. Невизначений, визначений та невласний інтеграли
1. Інтегрування дробово-раціональних функцій.
2. Інтегрування деяких тригонометричних функцій.
3. Інтегрування деяких ірраціональних функцій.
4. Інтегрування способом підстановки.
5. Інтегрування способом за частинами.
6. Означення визначеного інтеграла, його геометричний і фізичний зміст, умови існування. Обчислення визначених інтегралів за формулою Ньютона – Лейбніца. Наближене обчислення визначеного інтеграла.
7. Заміна змінної і інтегрування частинами у визначеному інтегралі.
8. Невласні інтеграли першого роду (з нескінченними межами інтегрування).
9. Невласні інтеграли другого роду (від функцій, необмежених на скінченому проміжку).
10. Застосування визначеного та невласних інтегралів до розв’язання деяких задач геометрії: обчислення площі плоскої фігури, довжини лінії, об’єму тіла обертання та площі поверхні обертання.
3. Ряди
Числові ряди. Збіжність і сума ряду. Необхідна умова збіжності. Ряди з додатними членами. Ознаки збіжності: ознаки порівняння Даламбера, інтегральна ознака Коші. Знакопочережні ряди. Абсолютна і умовна збіжність. Ознака Лейбніца.
Функціональні ряди. Область збіжності. Степеневі ряди. Радіус і інтервал збіжності. Властивості степеневих рядів.
Розвинення функцій в степеневі ряди. Ряди Тейлора і Маклорена. Застосування степеневих рядів до наближених обчислень.
Ряд Фур’є. Розвинення функцій у ряд Фур’є. Умови розвинення функцій в ряд Фур’є.
Список літератури
1. Пискунов Н.С. Дифференциальное и интегральное исчисление: Підруч-
ник в 2-х томах, т. I – М.: Інтеграл – Прес, 2002. – 416 с.
2. Вища математика. Збірник задач / За редакцією В.П.Дубовика,
І.І. Юрика. – Київ: Видавництво “А.С.К.”, 2003. – 480 с.
3. Вища математика. Збірник задач за редакцією П.П. Овчиннікова , ч. I,II,
Київ: Техніка, 2003 .– 380 с.
4. Дубовик В.П., Юрик І.І. Вища математика.– Київ, “А.С.К.”, 2005.–
648 с.
5. Данко П.Є., Попов А.Г., Кожевникова Г.Я. Вища математика у вправах
та задачах. Ч.I.– М.: Вища школа, 2000.– 420 с.
6. Дюженкова Л.І., Дюженкова О.Ю., Михалін Г.О. Вища математика.
Приклади і задачі.– Київ: Видавничий центр “Академік”, 2002.– 621 с.
ВЛАСТИВОСТІ НЕВИЗНАЧЕНОГО ІНТЕГРАЛА
а)
 .
.
б)
![]() .
.
в)
![]() .
.
а)
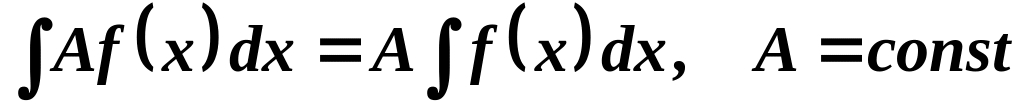 .
.
б)
![]() .
.
в)
![]() ,
якщо
,
якщо
![]() .
.
Інтегрування способом підстановки
![]() .
.
Інтегрування способом за частинами
![]() .
.
Таблиця невизначених інтегралів
 ;
8.
;
8.
 ;
;  ;
9.
;
9.
 ;
; 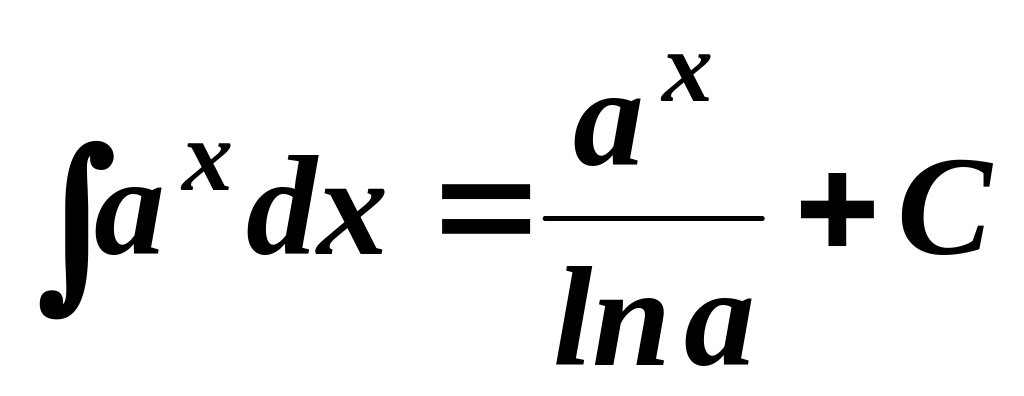 ;
10.
;
10.
 ;
;  ;
11.
;
11.
 ;
;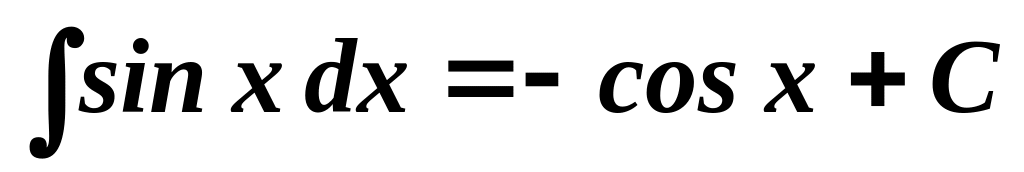 ;
12.
;
12.
 ;
; ;
13.
;
13.
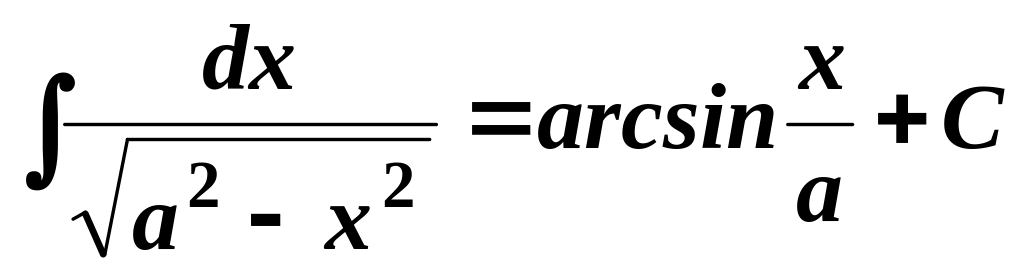 ;
;
7.
![]() ;
14.
;
14.
![]() .
.
Формула Ньютона - Лейбниця для обчислення визначених інтегралів
![]() .
.
Спосіб підстановки у визначених інтегралах
![]() .
.
Спосіб інтегрування за частинами у визначених інтегралах
![]() .
.
Формула Сімпсона для наближеного обчислення визначених
інтегралів
![]() ,
,
де
![]() -
парне число.
-
парне число.
Формули для розв’язування прикладних задач
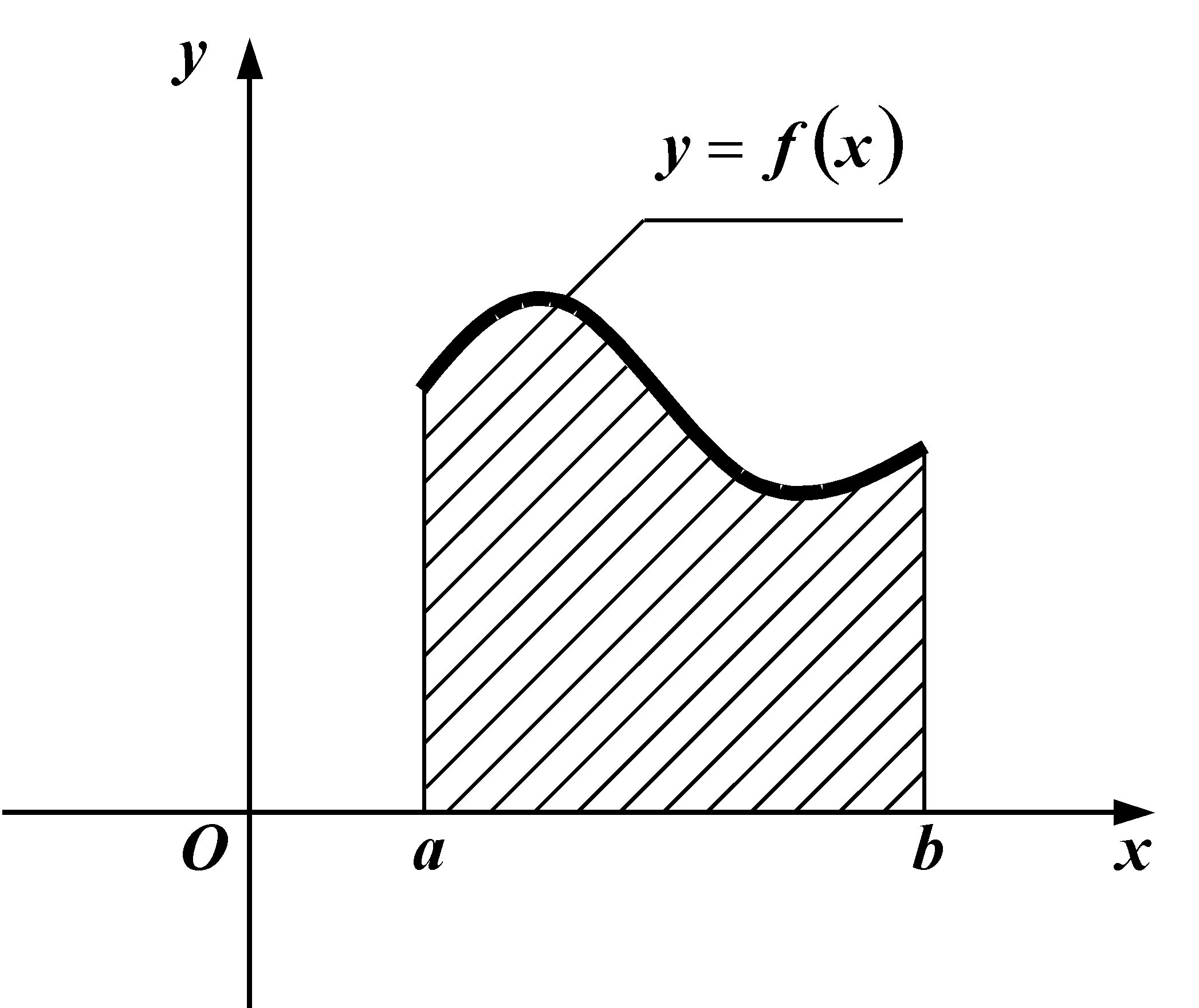
Площа плоскої фігури
а)
![]() ,
,
(криволінійної трапеції).
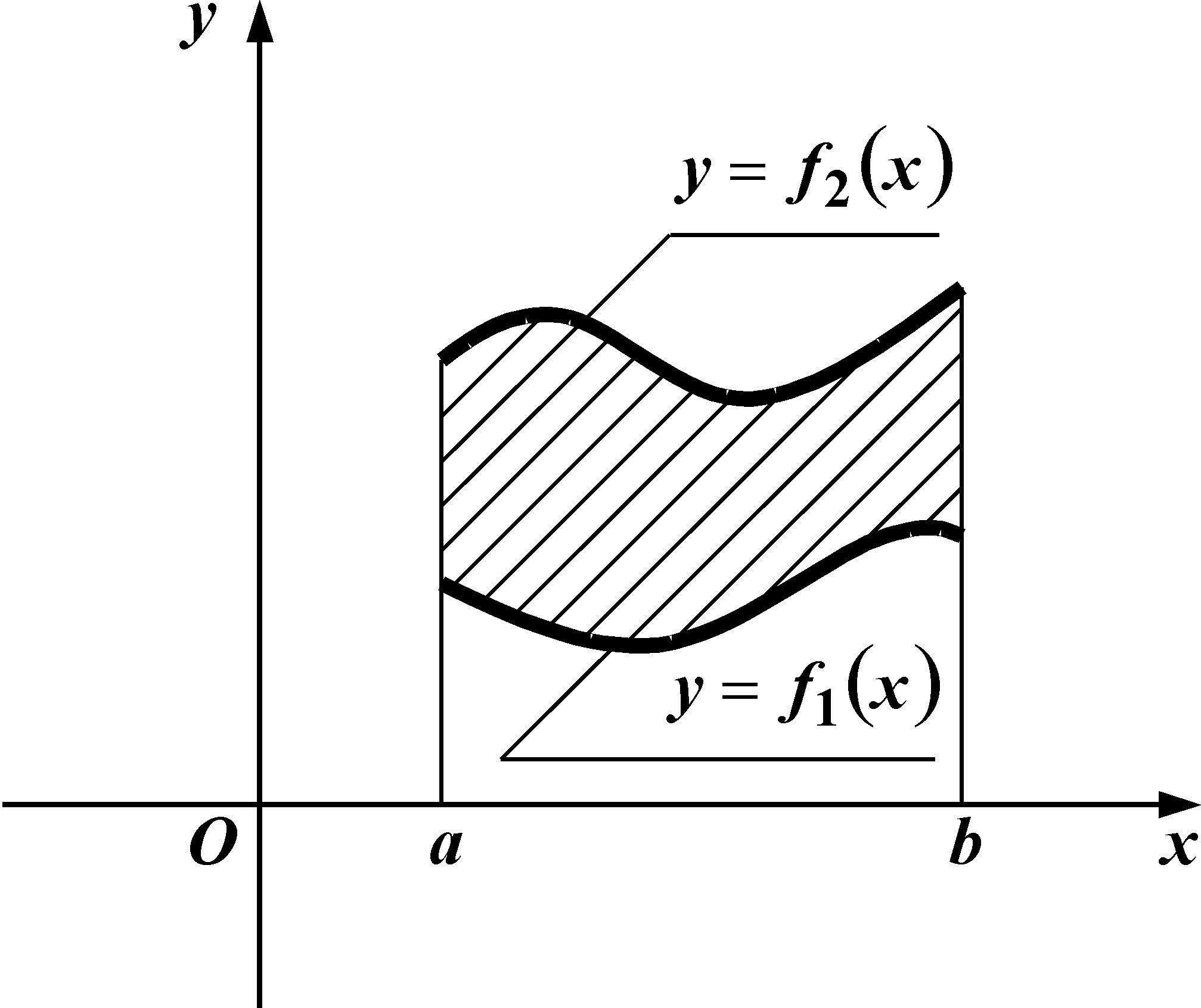
б)
![]() .
.
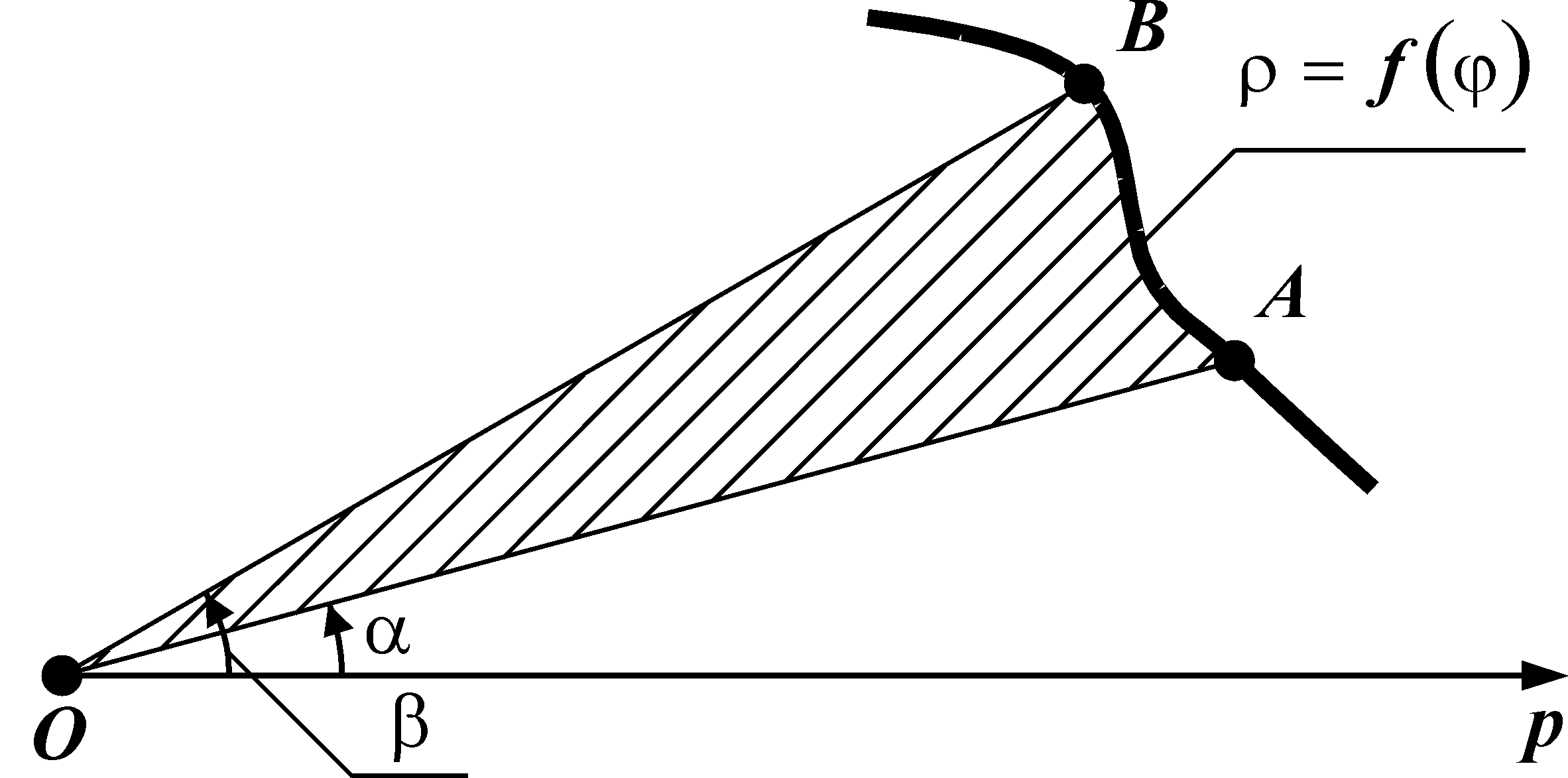
в)
![]() ,
(для криволінійного сектора).
,
(для криволінійного сектора).
````````````````````````
Довжина дуги
а)
![]() .
.
б)
![]() .
.
в)
 .
.
Об’єм тіл обертання
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4. Площа поверхні обертання
![]() .
.
5. Невласні інтеграли з безкінечними границями
![]() .
.
![]() .
.
![]() ,
де
,
де
![]() –довільне
значення,
–довільне
значення,
![]() – всюди
неперервна функція.
– всюди
неперервна функція.
Якщо
границя такого інтегралу є кінцевою,
то такий інтеграл називається збіжним;
у разі, коли інтеграл прямує до
![]() ,
його називають розбіжним.
,
його називають розбіжним.
6. Невласні інтеграли від розривних функцій
![]() ,
,
де
![]() –
точка розриву функції, де
–
точка розриву функції, де
![]() .
.
![]() .
.
