4.2. Обработка результатов

1. На основе результатов измерений, т.е. табл. 1, вычислить различные параметры контура и внести их в таблицу 2 в тех единицах, которые в ней указаны:

Таблица 2. Вычисляемые параметры колебательного контура.

	f, кГц	δ	Q	τ, мкс	L, мГн	r, Ом	, Ом	, Ом
С1=… нФ
С2=…нФ

Последовательность вычислений такова:

1. f=1/T;

2. δ – из формулы (11);

3. Q=π/δ;

4. τ=1/β;

5. L=1/(ω₀²С), где ω₀≈ω=2πf;

6. r – из формул (14) и (18) при R_маг=0;

7. − из формулы (18) при R_маг= ;

8. − из формулы (17).

2. Установить, можно ли затухание в контуре считать слабым (β≪ω₀). Для этого определяющее отношение ω₀/β удобно оценить из формулы (13), в которую подставляется полученное значение Q или δ.

3. Активное сопротивление обмотки катушки r в табл.2 для различных частот неодинаково, т.е. r=r(f). Это объясняется скин-эффектом − явлением вытеснения тока к поверхности проводника при повышении частоты. Поэтому при увеличении частоты активное сопротивление проводов растёт. Измерения, проведённые на постоянном токе (f=0), дали значение r=0,5 Ом (активное сопротивление в этом случае называется омическим).

По трём имеющимся точкам построить график r(f).

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Вывести дифференциальное уравнение, описывающее свободный ток в контуре RLC, и найти его колебательное решение i(t) при начальных условиях: i(0)=0, и(0)=U₀.

2. Дать определения логарифмического декремента затухания, времени релаксации, добротности, критического сопротивления.

3. при каком условии затухание считается слабым? Доказать. что при слабом затухании: а) Q≫1; б) 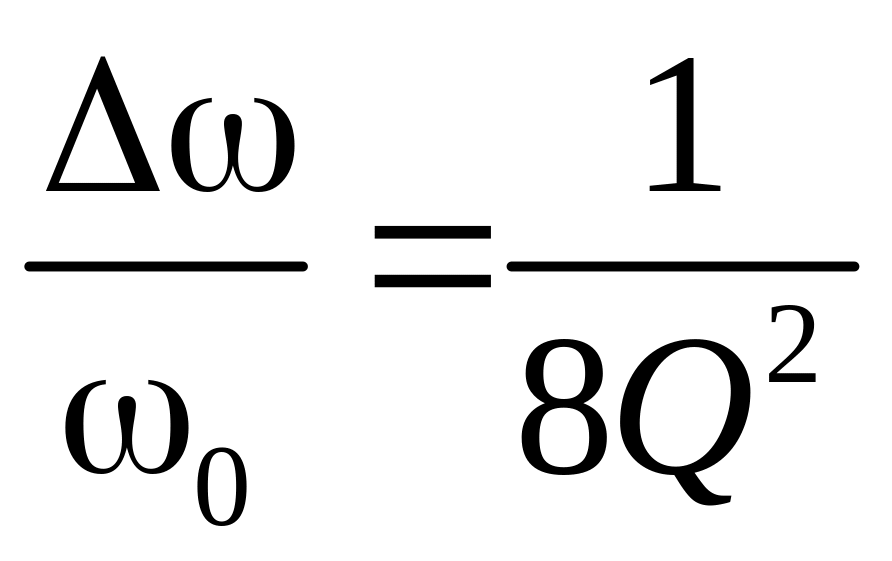, где ω₀ – собственная частота контура, Δω=ω₀−ω, ω – частота свободных колебаний в контуре.

4. Из формулы (16) получить выражение для тока i(t) при R=R_кр, изобразить соответствующий график i(t) и найти его максимум.

5. Что такое скин-эффект? Чем отличается активное сопротивление катушки от омического? А чем отличается активное от реактивного?

6. Согласно (14), при уменьшении ёмкости С добротность контура должна расти как 1/ ; почему же этого не наблюдается в данной работе?

7. Вывести формулу (11).

8. Обосновать выбор периода и длительности возбуждающих контур импульсов.

9. Через сколько колебаний N амплитуда тока в контуре RLC уменьшится в р=20 раз, если R=1 Ом, L=10 мГн, С=1 мкФ ?

10. Через N=30 колебаний их амплитуда уменьшилась в р=20 раз. Определить добротность контура.

11. Добротность контура Q=32. Сколько колебаний произойдёт в контуре за время релаксации?

12. Используя определение добротности (15), найти. какую среднюю мощность Р надо подводить к контуру RLC, в котором R=1 кОм, L=12 мГн, С=6 нФ, чтобы поддерживать в нём колебания с амплитудой напряжения на конденсаторе U=6 В ? Ответ. Р=CU²R/(2L)=9 мВт.

13. Когда сыр небрежно положили на чашку торговых пружинных весов, стрелка, качаясь с затуханием около равновесия, показала в трёх последовательных крайних отклонениях 600, 300 и 500 г. Определить массу сыра, полагая затухание весов достаточно слабым. Оценить время, за которое при такой небрежности колебания стрелки успокоятся до ±10 г, если период качаний стрелки Т=1,6 с. Ответ. m=400 г; Q=4, t=5,7 с.

1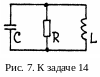 4. Определить частоту свободных колебаний напряжения в цепи RLC, показанной на рис. 7 (величины R, L и C заданы). Найти добротность Q такой колебательной системы. При каком сопротивлении R колебания в этой цепи станут невозможны (т.е. найти её критическое сопротивление)?

Ответ. , где , ; ;

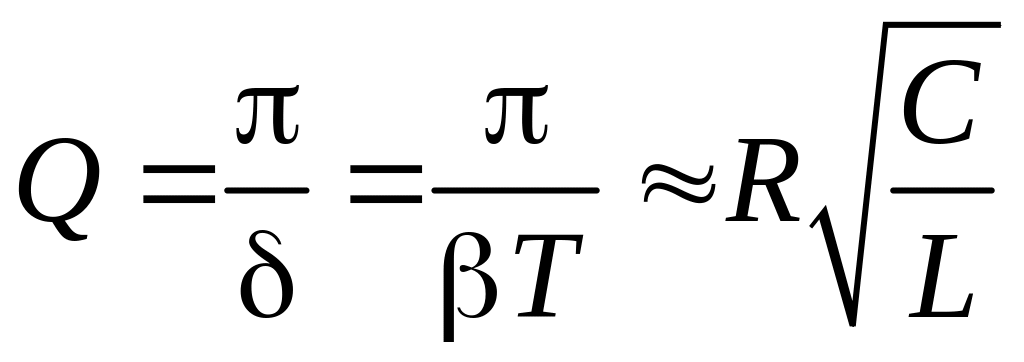R_кр= (при β²= ).

ЛИТЕРАТУРА

1. Калашников С. Г. Электричество. – М.: Наука, 1977. – §§ 134, 208-210.

2. Савельев И. В. Курс общей физики, т.2.– М.: Наука, 1982. – §§ 63, 90.

3. Иродов И. Е. Основные законы электромагнетизма. – М.: Высшая школа, 1983. – §§ 11.1, 11.2.

Работа № Ф310