3. Колебания и волны

Работа № Ф309

Свободные колебания

Цель работы – измерение параметров свободных затухающих колебаний в контуре RLC с помощью осциллографа; определение условий существования колебательного и апериодического режимов в контуре.

1. Введение

Колебания – это периодический процесс, в котором значения какой-либо физической величины х точно или приближённо повторяются через равные промежутки времени Т, называемые периодом колебаний.

Среди различных видов колебаний наиболее часто встречаются синусоидальные (гармонические), описываемые функциями синуса или косинуса. Колебания называются свободными, если они происходят в первоначально выведенной из равновесия системе без дальнейшего поступления в неё энергии от внешних источников. Если же колебания в системе поддерживаются периодическим поступлением в неё энергии извне, то они называются вынужденными. Свободные колебания реальных механических и электрических систем всегда являются затухающими, т.е. с убывающей до нуля амплитудой. При этом первоначально запасённая колебательной системой энергия в конечном итоге превращается в тепло.

Простейшей реальной электрической колебательной системой является колебательный контур – замкнутая цепь, состоящая из катушки индуктивностью L, конденсатора ёмкостью С и резистора с активным сопротивлением R – контур RLC. Элементы L и С называются реактивными элементами контура, а элемент R – активным элементом. Часто резистор как отдельный физический элемент в таком контуре отсутствует, но активное сопротивление контура всё равно остаётся отличным от нуля – это внутреннее сопротивление проводов катушки, которое к тому же может заметно зависеть от частоты колебаний вследствие скин-эффекта.

2. Описание свободного процесса в контуре

Пусть в каком-либо реактивном элементе контура создан первоначальный запас энергии W₀: это может быть, например, первоначальный ток I₀, возбуждённый в катушке, или первоначальное напряжение U₀ на конденсаторе. Если после этого контур предоставить самому себе, то в нём будет протекать свободный процесс – колебательный или апериодический, − в зависимости от соотношения между параметрами R, L и С. Для описания этого процесса исходным является второе уравнение Кирхгофа u_L+u_R+u_C=0 (рис. 1), где:

u_L= − напряжение на индуктивности,

и _R=Ri – напряжение на активном сопротивлении,

и_С= − напряжение на ёмкости,

i – ток в контуре, q – заряд на конденсаторе.^)

Таким образом,

. (1)

Это уравнение можно продифференцировать по t, и тогда, поскольку, dq/dt=i, получим 65дифференциальное уравнение 2-го порядка для тока:

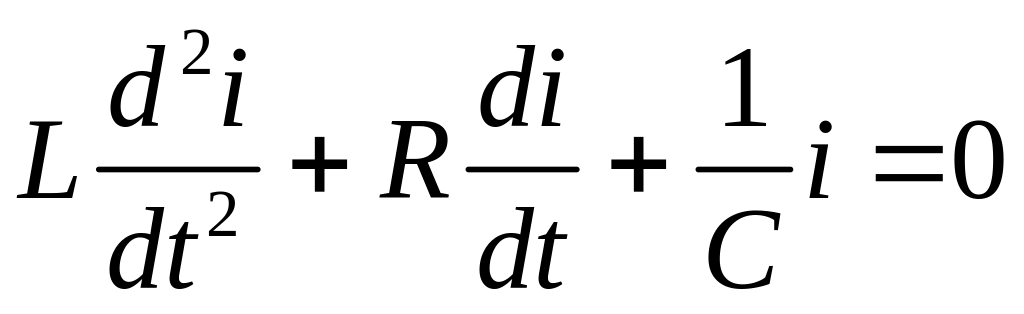. (2)

А можно преобразовать (1) подстановками: , q=Cи_С, т.е. . Легко видеть, что это даст точно такое же дифференциальное уравнение для напряжения на конденсаторе:

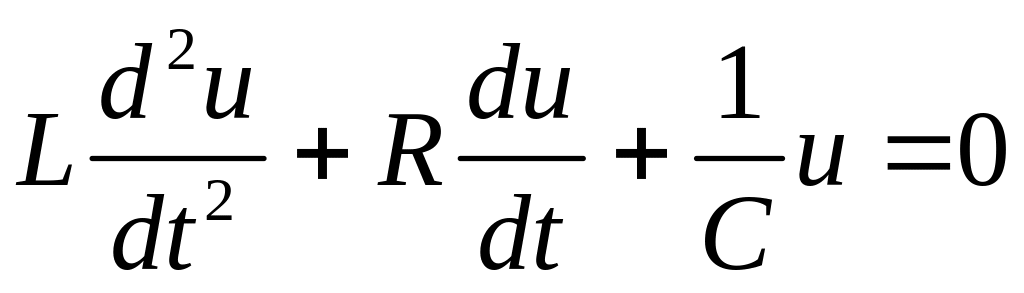(3)

(здесь и далее индекс у напряжения на конденсаторе опущен, т.е. и≡и_С). Поскольку уравнения (2) и (3) эквивалентны, то рассмотрим, для определённости, (3). Если, решив его, мы найдём и(t), то сразу же получим и ток в контуре: i=С , т.е. уже не будет необходимости решать и уравнение (2).

Представим уравнение (3) в каноническом виде:

, (4)

где обозначено: , , . Величина β называется коэффициентом затухания, а ω₀=1/ − собственной частотой колебательного контура. Для решения уравнения (4) введём новую переменную х, полагая

и=хе^−βt. (5)

Подставляя это в (4), получим:

. (6)

Формально (6) совпадает с уравнением свободных незатухающих колебаний в идеальном контуре LC: , однако там коэффициент при х всегда положителен, а здесь величина может принимать любые действительные значения. Поэтому рассмотрим по отдельности три возможных варианта.

ВАРИАНТ 1: >0.

Обозначив =ω², получаем:

.

Это уравнение свободных незатухающих колебаний, и его общее решение может быть записано в виде:

.

Следовательно, с учётом (5), общим решение уравнения (4) будет функция

. (7)

Коэффициенты А и В здесь определяются начальными условиями, т.е. значениями тока и напряжения в контуре при t=0. Пусть в начальный момент времени конденсатор был заряжен до напряжения U₀, а ток в контуре отсутствовал. Тогда начальные условия будут иметь вид:

и(0)=U₀, i(0)=C .

Подставляя их поочерёдно в (7) и решая полученную систему двух уравнений относительно А и В в приближении β≪ω₀, находим: А=U₀, В≈0. Следовательно, напряжение на конденсаторе будет меняться по закону

и(t)=U₀ . (8)

С вободный процесс, описываемый функцией (8), называется затухающими колебаниями (рис. 2). Эта функция, строго говоря, не является периодической, но она периодически, т.е. через одинаковые интервалы времени и бесконечное число раз, походит через ноль. Величина

(9)

− это угловая частота затухающих колебаний (далее просто – частота); видно, что она меньше собственной частоты ω₀, однако практически в большинстве случаев β≪ω₀, и поэтому обычно считается, что ω≈ω₀.

Для описания затухающих колебаний в контуре вводятся следующие понятия и параметры:

1. Период. Величина Т=2π/ω называется периодом затухающих колебаний. При ω≈ω₀ период Т≈2π .

2. Амплитуда. Экспоненциально убывающий множитель

,

стоящий в (8) перед периодической функцией, называется амплитудой затухающих колебаний (рис. 2).

3. Время релаксации. Время τ, за которое амплитуда убывает в е=2,718 раз, называется временем релаксации, или постоянной времени затухающих колебаний. В соответствии с этим определением,

, отсюда .

4. Логарифмический декремент затухания. Натуральный логарифм отношения двух «соседних амплитуд», (т.е. амплитуд, взятых через период) называется логарифмическим декрементом затухания δ (рис. 2):

.

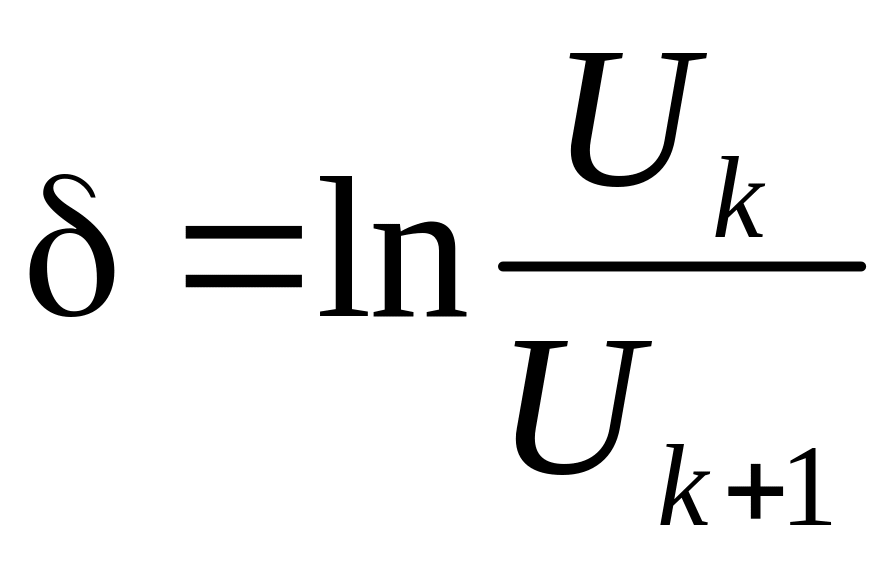В соответствии с этим определением,

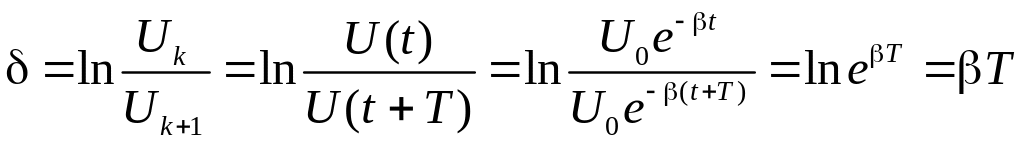. (10)

На основе этого определения несложно показать, что если измерить некоторую амплитуду U_k и следующую за ней через N периодов U_k+N, то логарифмический декремент затухания можно определить по формуле:

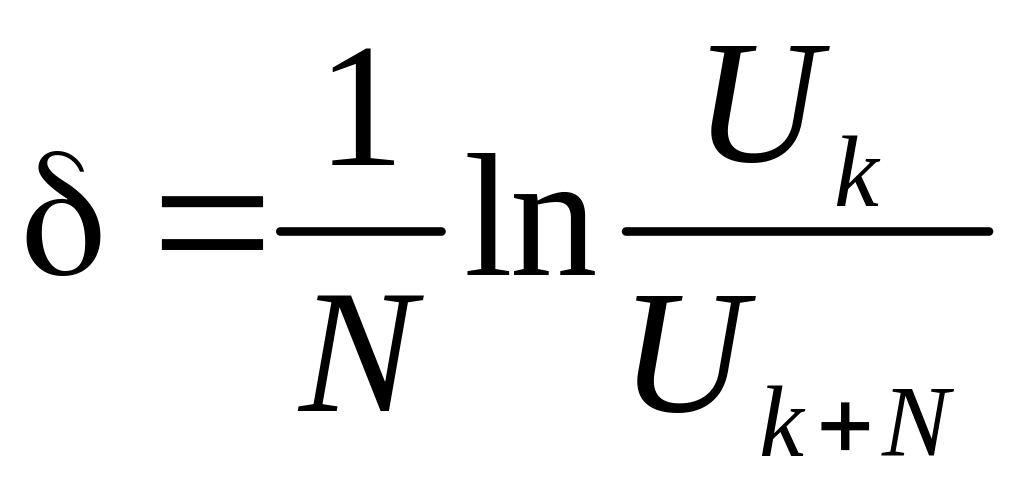. (11)

5. Слабое затухание. Затухание называется слабым, если β≪ω₀. Символ « ≪ » обычно означает, что меньше, по крайней мере, на порядок. Из (9) следует, что при слабом затухании ω≈ω₀, т.е. частота свободных колебаний ω практически равна собственной ω₀=1/ .

6. Добротность. Важной характеристикой колебательного контура является его добротность Q. Добротность можно определить несколькими эквивалентными способами. Наиболее простое определение такое:

Q= , (12)

т.е. это величина, обратная логарифмическому декременту затухания с множителем π. Добротность является полезной характеристикой контура лишь при слабом затухании; в этом случае

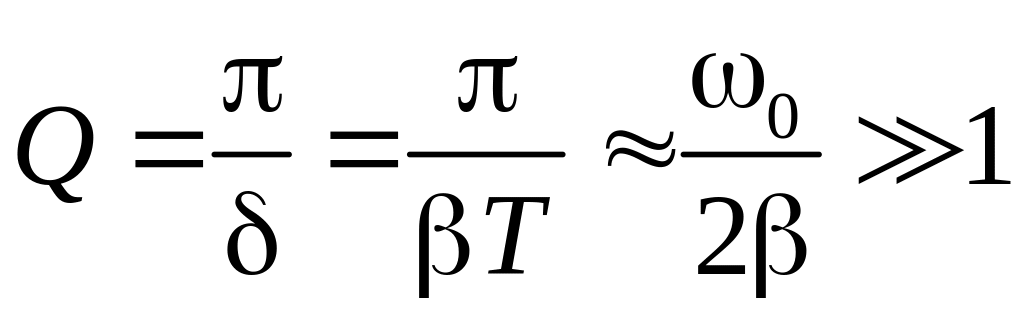. (13)

Для хороших радиоконтуров Q~20…100; у объёмных резонаторов на СВЧ добротность может достигать нескольких десятков тысяч. Если в (13) подставить ω₀= и β= , то получим, что при слабом затухании добротность контура Q простым соотношением выражается через его первичные параметры R, L и С:^)

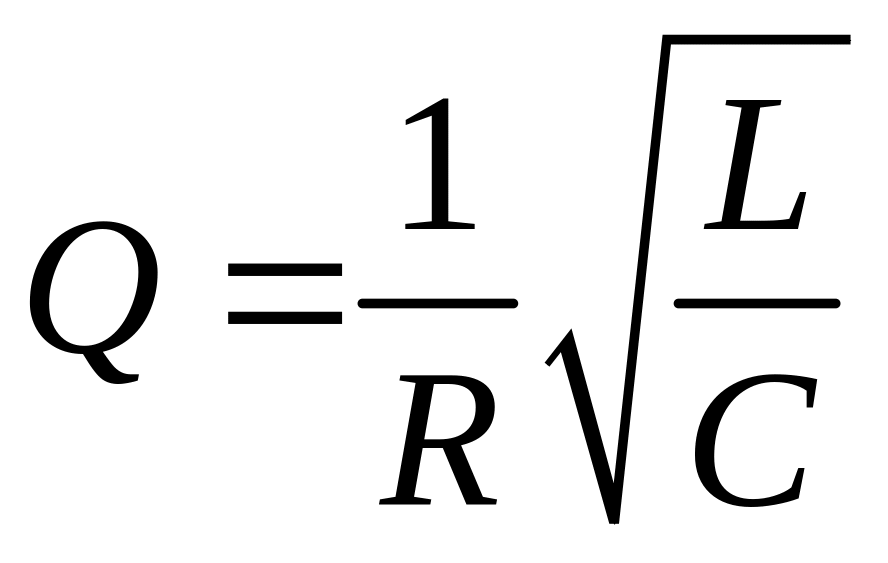. (14)

Есть ещё одно полезное определение добротности, эквивалентное (12):

добротностью контура называется отношение энергии W, запасённой в его реактивных элементах L и С в данный момент, к её убыли ΔW_T за текущий период, умноженное на 2π:

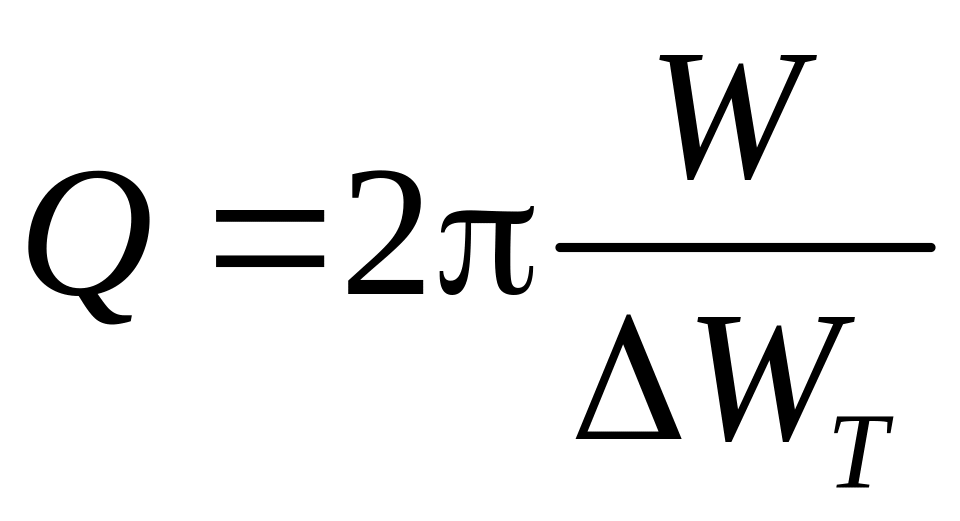. (15)

Покажем, что в случае слабого затухания определения (15) и (12) эквивалентны. При медленно убывающей функции W(t), т.е. когда за период

ΔW_T= , убыль ΔW_T можно представить в виде:

ΔW_T=− .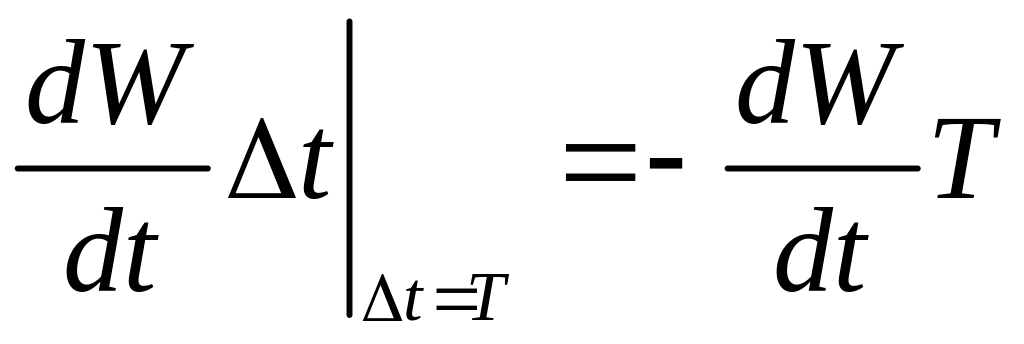

Полагая здесь , где W₀ – первоначальный запас энергии в контуре, с учётом (10) получаем:

.

ВАРИАНТ 2: =0.

В этом случае уравнение (6) вырождается в тривиальное: , общее решение которого имеет вид: х=Аt+В. Тогда, с учётом (5),

.

Если начальные условия те же, что и в варианте 1, то В=U₀, А=βU₀, и тогда

. (16)

Кривая (16) апериодична (рис. 3). Это означает. что если активное сопротивление контура достигает некоторой величины R_кр, называемой к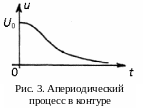 ритическим сопротивлением, то колебательный процесс в нём становится невозможным: первоначально заряженный конденсатор при этом просто экспоненциально разряжается через достаточно большое сопротивление R=R_кр. Величина такого сопротивления определяется из условия , откуда

R=R_кр=2 . (17)

ВАРИАНТ 3: <0.

Общее решение уравнения (6) в этом случае будет иметь вид:

,

где . С учётом (5) и при тех же начальных условиях получаем:

.

Качественно эта зависимость имеет такой же вид, как и на рис. 3, только с ещё большей скоростью убывания функции и(t).