11. Передаточная функция звена

Отношение изображения по Лапласу выходного сигнала линейного звена к изображению по Лапласу входного сигнала, при нулевых начальных условиях, называют передаточной функцией линейного звена:

. (2.4)

Здесь p - это комплексная переменная, которую можно представить в виде: , Y(p) – изображение по Лапласу выходного сигнала, X(p) – изображение по Лапласу входного сигнала.

В дальнейшем мы часто будем представлять передаточную функцию в виде:

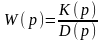, где K(p) и D(p) – полиномы комплексной переменной p, порядка m и n, соответственно. Для рассматриваемых в ТАУ систем, справедливо выражение: mn. Если вместо комплексной переменной p подставить в выражение для W(p) чисто мнимое выражение jw, то получим комплексный коэффициент передачи W(jw).

12. Временные характеристики звена.

Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Во-первых, это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств. Во - вторых, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины.

Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и гармоническое воздействия. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий u_i(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить результирующее изменение выходной величины y(t).

Временные характеристики представляют собой зависимость выходного сигнала системы от времени при подаче на ее вход некоторого типового воздействия. В ТАУ используются два вида временных характеристик:

- переходная характеристика (переходная функция);

- импульсная переходная характеристика (функция веса).

Переходной характеристикой h(t) называется зависимость выходного сигнала системы от времени при подаче на ее вход единичного ступенчатого воздействия 1(t) (рис.1.2) Данное входное воздействие определяется выражением g(t)

(1.18) 1 Рис.1.2

0 t

Изображение по Лапласу единичного ступенчатого воздействия

будет

Обозначим изображение переходной функции как H(s), а передаточную функцию системы как W(s) и получим .

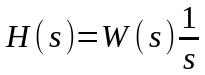Переходная функция может быть определена по ее изображению использованием формулы обратного преобразования Лапласа, в частности с помощью таблиц преобразования Лапласа.

Импульсной переходной характеристикой (ИПХ) или функцией веса системы w(t) называется зависимость выходной величины от времени при подаче на вход воздействия в виде дельта-функции (t -), которая определяется следующим образом:

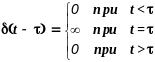(1.21)

Функция веса системы может быть определена так же, как и переходная функция, или путем дифференцирования переходной функции.

Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристиками системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии.

Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной функции можно найти из формулы Хевисайда:

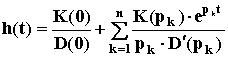, где p_k - корни характеристического уравнения D(p) = 0. Взяв производную от переходной функции можно получить выражение для импульсной переходной функции (t) = h’(t).

h(t) (t)

k k

T

t t

Рис. 1.6. Переходная функция. Рис.1.7. Функция веса.

КРАТКО: есть типовые воздействия на систему: ступенчатое, импульсное, гармоническое. Временные хар-ки – зависимость вых. сигнала от времени при подаче в систему типовых воздействий. Используются две такие хар-ки: переходная функция (хар-ка) и импульсная перех. хар-ка.

Переходная характеристика – зависимость выходного сигнала от времени при подаче единичного ступенчатого возд-ия 1(t).

Переходная импульсная характеристика – тоже зависимость вых. величины, но уже от подачи на вход воздействия в виде дельта-функции.

Перех. хар-ку можно получить, если есть перед. функция. Перех. имп. хар-ку можно получить как производную перех. функции.