Вопрос 36.

Выделение области устойчивости САУ

Вариант1.

Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.

При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению, будет перемещаться по некоторой траектории, например из положения N в положение M. Этому перемещению будет соответствовать и перемещение корней (p_N1, p_N2, p_N3) на комплексной плоскости в положение (p_M1, p_M2, p_M3).

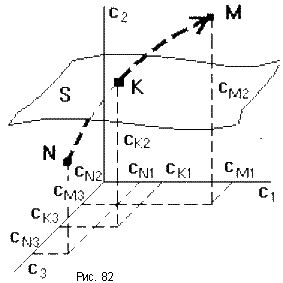
При этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k-й корень примет значение p_K = j _K, а коэффициенты уравнения будут иметь определенные значения c_K1, c_K2, c_K3, определяющие в пространстве коэффициентов точку K. Подставим корень p_K в характеристическое уравнение, получим тождество:

 

D(p_K ) = (j _K)³ + cK1(j _K)² + c_K2 (jK ) + c_K3 = 0

Меняя от - до + и находя при каждой частоте все возможные сочетания коэффициентов c₁ ,c₂ ,...,c_n , удовлетворяющих уравнению

 

D(j ) = (j )ⁿ + c₁ (j )^n-1 + c₂ (j )^n-2 + ... + c_n = 0,

 

можно построить в n-мерном пространстве коэффициентов сложную поверхность S, разделяющую его на области, называемые D-областями. Полученное уравнение называется уравнением границы D-разбиения.

Переход из одной D-области в другую через поверхность S соответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть, каждая точка внутри определенной D-области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначают D(m) по числу m правых корней.

Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S, можно выявить обозначения всех других областей. Особый интерес представляет область D(0), которой соответствуют уравнения с полным отсутствием правых корней, называемая областью устойчивости. Описанный метод определения областей устойчивости называется методом D-разбиений.

Вариант 2.

На практике проектировщиков систем автоматического управления интересует пространство (область, пределы, диапазон) параметров, при которых системы является устойчивой. Множество значений параметров, при которых система обладает свойством устойчивости, называется областью устойчивости системы. Для определения областей устойчивости имеется несколько методик. На основе алгебраического критерия устойчивости Гурвица;

Метод Д-разбиения; Метод корневого годографа.

Область устойчивости по Гурвицу определяется с помощью использования равенств в условиях Гурвица вместо неравенств. Чаще всего определение границы искомой области может быть произведено при условии  . (Смотри пункт "Определение критического коэффициента усиления"). Отсюда определяется зависимость интересующего нас параметра  от параметра . Получаемая зависимость ()- граница области устойчивости системы. В системах более высоких порядков возникает необходимость рассмотрения других миноров. При этом область устойчивости может сужаться.