
Введи частицу — получишь результат
Для создания работоспособного топологического квантового компьютера необходимо продумать механизм установки исходного значения кубитов, а также процедуру считывания получаемых результатов. На этапе инициализации создаются пары квазичастиц. Проблема в том, чтобы узнать, какая их разновидность была создана. Обычно к созданным парам направляют пробные энионы, а затем измеряют, как они изменились, т.к. это зависит от типа частиц, вблизи которых они прошли. (Если пробный энион изменился, то он не будет полностью аннигилировать со своим партнером.) Пары энионов неподходящего типа следует просто отбрасывать.
На этапе считывания также производится измерение состояний энионов. Если они далеко отстоят друг от друга, то провести измерение невозможно: энионы должны поступать парами. Грубо говоря, требуется выяснить, полностью ли аннигилируют пары (как истинные античастицы), или после их взаимодействия остаются заряды и потоки, показывающие, как состояния были изменены при переплетении по сравнению с точным отношением античастиц, с которого начался процесс. К сожалению, нельзя сказать, что топологический компьютер полностью нечувствителен к ошибкам. Главный их источник — тепловые колебания в материале подложки, при которых может возникнуть дополнительная пара энионов. Она вплетается в косу вычисления, а в конце снова аннигилирует. К счастью, процесс тепловой генерации подавляется низкой температурой, при которой работает топологический компьютер. Кроме того, вероятность возникновения ошибки убывает по экспоненте по мере увеличения расстояния, проходимого нарушителями. Таким образом, можно достигнуть любой необходимой степени точности, создавая достаточно большой компьютер и удерживая работающие энионы в ходе плетения кос вполне обособленными.
По оценкам разработчиков, частота ошибок в логическом элементе «НЕ» не будет превышать 10-30
Пока мы стоим у колыбели топологических квантовых вычислений. Существование основных рабочих элементов, неабелевых энионов, еще не демонстрировалось, кроме того, требуется создать базовые логические элементы. В упомянутом выше эксперименте Фридман, Дас Сарма и Найяк могли бы достичь обеих целей: если бы их энионы действительно оказались неабелевыми, устройство могло бы выполнять логическую операцию «НЕ» над состоянием кубита. По оценкам исследователей, частота ошибок не будет превышать 10-30, поскольку вероятность их возникновения экспоненциально убывает с понижением температуры и увеличением размеров устройства. Экспоненциальная зависимость — существенный вклад топологии, не имеющий аналогов в традиционных подходах к квантовым вычислениям.
Именно чрезвычайно низкая частота ошибок делает топологические квантовые вычисления столь привлекательными. Кроме того, технология создания устройств с дробным квантовым эффектом Холла хорошо отработана при производстве микросхем. Единственное необычное условие — чрезвычайно низкие температуры (порядка 1 мК), при которых должны работать устройства, чтобы волшебные квазичастицы оставались устойчивыми.
Если неабелевы энионы действительно существуют, топологические квантовые компьютеры вполне могут опередить обычных квантовых собратьев в гонке от отдельных кубитов и логических элементов к полностью укомплектованным машинам, по праву заслуживающим названия «компьютер».
ТОПОЛОГИЧЕСКИЕ ОШИБКИ |
Д ЛОГИЧЕСКИЙ ЭЛЕМЕНТ «НЕ» Рассмотрим логический элемент «НЕ», основаный на дробном квантовом состоянии Холла с энионами, имеющими заряд, равный одной четверти заряда электрона. Электроды создают два островка, на которых удерживаются энионы. Ток течет вдоль границы, но при подходящих условиях может туннелировать поперек узких перешейков. 1. Сначала на один островок помещают два эниона (синие), затем прикладывают напряжение, чтобы переместить один из них на другой островок. Полученная пара энионов представляет собой кубит в исходном состоянии, которое можно определить, измеряя ток, текущий по ближайшей границе. |
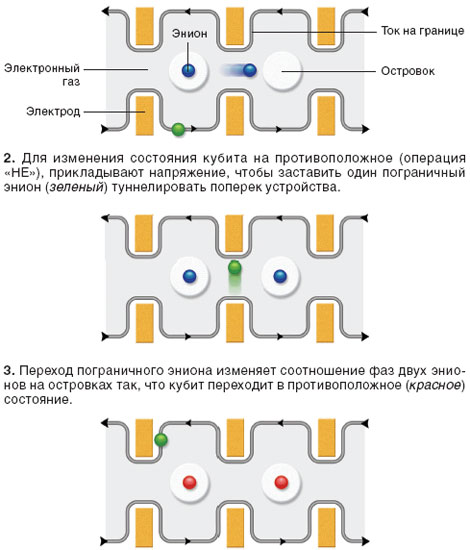
![]()

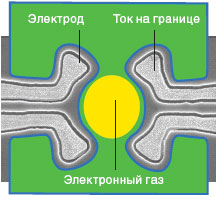 ЕТЕКТОР
ЭНИОНОВ
Владимир Голдман
использовал устройство, изображенное
на цветной микрофотографии, чтобы
показать, что некоторые квазичастицы
(возбуждения в квантовом состоянии
Холла) ведут себя как энионы. Прибор
был охлажден до 10 мК и помещен в сильное
магнитное поле. Между четырьмя
электродами образовался двухмерный
электронный газ с различными типами
квазичастиц в желтой и зеленой областях.
Характеристики пограничного тока
свидетельствовали о том, что квазичастицы
на желтом островке были энионами.
ЕТЕКТОР
ЭНИОНОВ
Владимир Голдман
использовал устройство, изображенное
на цветной микрофотографии, чтобы
показать, что некоторые квазичастицы
(возбуждения в квантовом состоянии
Холла) ведут себя как энионы. Прибор
был охлажден до 10 мК и помещен в сильное
магнитное поле. Между четырьмя
электродами образовался двухмерный
электронный газ с различными типами
квазичастиц в желтой и зеленой областях.
Характеристики пограничного тока
свидетельствовали о том, что квазичастицы
на желтом островке были энионами.