Косы и логические элементы

Располагая неабелевыми энионами, можно создать физическое представление группы кос — математической структуры, описывающей все способы, которыми можно переплести данный набор нитей. Любую косу можно построить из ряда элементарных операций, в которых две смежные нити перемещаются либо по часовой стрелке, либо против нее. Каждая возможная последовательность манипуляций с энионами соответствует косе и наоборот. Кроме того, каждой косе соответствует сложная матрица, получающаяся в результате объединения всех матриц перестановки энионов.

Теперь рассмотрим, как косы связаны с квантовыми вычислениями. Состояние обычного компьютера характеризуется совокупностью состояний всех его битов — последовательностью нулей и единиц в регистрах. Точно так же состояние квантового компьютера определяется состоянием всех его кубитов. В топологическом квантовом компьютере кубиты можно представить группами энионов. В квантовом компьютере процесс перехода от начального состояния к конечному описывается матрицей, которая умножается на объединенную волновую функцию всех кубитов. Сходство с тем, что происходит в топологическом квантовом компьютере, очевидно: в данном случае это матрица, относящаяся к конкретной косе, соответствующей последовательности манипуляций с энионами. Таким образом, операции с энионами приводят к квантовому вычислению.

Сможет ли топологический квантовый компьютер выполнить любое вычисление, доступное обычному квантовому компьютеру? Фридман, Майкл Ларсен (Michael Larsen) из Университета штата Индиана и Чженгхан Ванг (Zhenghan Wang) из Microsoft доказали в 2002 г., что топологический квантовый компьютер действительно может моделировать любое вычисление стандартного квантового компьютера, но только приблизительно. Тем не менее, всегда можно найти такую косу, которая моделирует требуемое вычисление с любой заданной точностью. Правда, чем выше требуемая точность, тем больше число переплетений в косе. К счастью, число переплетений растет очень медленно, и достигнуть достаточно высокой точности не так уж трудно. Однако в упомянутом доказательстве не указано, как определить, какая именно коса соответствует нужному вычислению, — это зависит от конкретной структуры топологического квантового компьютера и, в частности, от разновидности используемых энионов и их связи с элементарными кубитами.

Чем выше требуемая точность вычислений, тем больше переплетений в косе

В 2005 г. проблемой обнаружения кос, выполняющих определенные вычисления, занимались Николас Боунстил (Nicholas E. Bonesteel) вместе с коллегами из Университета штата Флорида и лаборатории Lucent Technologies фирмы Bell Labs. Группа наглядно показала, как построить логический элемент «управляемое НЕ» (CNOT), работающий с точностью до 2·10^-3, с помощью косы из шести энионов. У элемента CNOT два входа: бит управления и целевой бит. Если бит управления равен единице, то целевой бит изменяется с нуля на единицу и наоборот. В противном случае биты не меняются. Действуя на кубиты с помощью сети из элементов CNOT и операции умножения отдельных кубитов на комплексную фазу, можно построить любое вычисление. Это лишний раз подтверждает, что топологические квантовые компьютеры могут справиться с любым квантовым вычислением.

Может ли топологический компьютер оказаться мощнее обычного квантового? К сожалению, нет. Фридман, Китаев и Ванг доказали, что работу топологического квантового компьютера можно эффективно моделировать с произвольной точностью на обычном квантовом компьютере, а значит, все, что может вычислить топологический квантовый компьютер, под силу и обычному квантовому. Наверняка все достаточно развитые вычислительные системы, использующие квантовые средства, обладают в точности одинаковыми вычислительными возможностями. (Аналогичный тезис для классических вычислений был предложен Алонсо Черчем (Alonzo Church) и Аланом Тьюрингом (Alan Turing) в 30-х гг. XX в.)

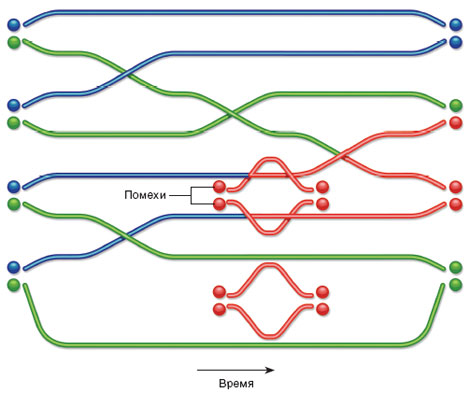
ПРЕДОТВРАЩЕНИЕ СЛУЧАЙНЫХ ОШИБОК

Ошибки в топологических расчетах возникают тогда, когда тепловые флуктуации приводят к появлению паразитных пар энионов, которые вплетаются в косу (красные линии) и искажают процесс вычисления. Однако вероятность такого вмешательства убывает по экспоненте с увеличением расстояния между энионами. Частоту ошибок можно свести к минимуму, удерживая участвующие в вычислении энионы достаточно далеко друг от друга (нижняя пара).