35) Геометрический закон распределения и его характеристики, пример.

Дискретная случайная величина X имеет геометрическое распределение с параметром p, если она принимает значения 1, 2, …, k, … (бесконечное, но счетное число значений) с вероятностями P(X=k) = p(1-p)^k-1

Характеристики:

1. Математическое ожидание случайной величины X, имеющей геометрическое распределение, равно M(X)= 1/p;

2. Дисперсия случайной величины X, имеющей геометрическое распределение, равна D(X)= (1-p)/p2 ;

3. Среднее квадратичное отклонение случайной величины X, имеющей геометрическое распределение равно σx=√D(X)=√(1-p) ⁄p.

1.M(X)=

2.D(X)=

3.σ_x= =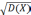

Пример:

Проводится проверка большой партии деталей, до обнаружения плохой детали. Без ограничения числа проверок. Составить закон распределения проверенных деталей. Найти мат. ожид. и дисперсию. Вероятность брака=0,1.

Х-число проверенных деталей, до обнаружения 1ой бракованной

p=0,1 q=0,9

xi	1	2	3	…..	k
pi	0,1	0,09	0,081	…..	0,1*99k-1

M[X]=10 D[X]=90 σ=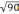

36) Закон распределения Пуассона и его характеристики, пример.

Дискретная случайная величина X имеет закон распределения Пуассона с параметром λ, если она принимает значения 0, 1, 2, …, k, … (бесконечное, но счетное число значений) с вероятностями P(X=k) = 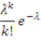= Pk(λ).

Пусть производится определенное число n независимых опытов. В каждом из них с одной и той же вероятностью р может наступить некоторое событие А. Рассматривается случайная величина X – число наступлений события А в n опытах. Устремим n к бесконечности и пусть при этом вероятность р стремится к нулю, причем λ = np будет величиной постоянной.

Тогда случайная величина X будет распределена по закону Пуассона, который имеет вид:

Значения X	0	1	2	…	n	…
Вероятности	p0	p1	p2	…	pn	…

Где рk = 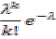(k=0, 1, 2,…).

Распределение Пуассона является предельным для биномиального распределения при указанных условиях и носит название закона редких явлений.

37) Равномерный закон распределения и его характеристики, пример.

Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне этого отрезка, т.е.

График плотности распределения вероятности непрерывной случайной величины X, имеющей равномерный закон распределения, выглядит так:

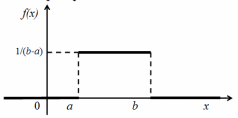
График функции распределения вероятности непрерывной случайной величины X, имеющей равномерный закон распределения, выглядит так:

Среднее квадратичное отклонение случайной величины X, имеющей равномерный закон распределения, равно σx=(b-a)⁄2√3.

Медиана случайной величины X, имеющей равномерный закон распределения, равна mx=(a+b)⁄2.