30) Свойства математического ожидания.

Математическим ожиданием или средним значением дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений, т.е. М[Х]=x1p1+x2p2+…+xnpn+….

Свойства:

1.Мат. ожид. постоянная величина = самой постоянной M[C]=C

2.Постоянное множество можно выносить за знак мат. ожид. M[K*X]=K*M[X]

3.Суммы двух случайных величин = сумме их мат. ожид. M[X+Y]=M[X]+M[Y]

4.M[X*Y]=M[X] * M[Y]

5.M[X+C]=M[X] + C

6.M[X-M(X)]=0

31) Дисперсия дискретной и непрерывной случайной величин. Среднее квадратичное отклонение.

Дисперсией называется математическое ожидание квадрата ее отклонения от математического ожидания. D[X]=M[X-M(X)]²

Е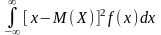 сли f(x) – плотность распределения непрерывной случайной величины, то

D(X)=

называется дисперсией этой случайной величины.

Средним квадратичным отклонением (стандартным отклонением) σx случайной величины Х называется арифметическое значение квадратного корня из ее дисперсии, т.е. ơx=√D[X].

32) Свойства дисперсии.

Теорема 6.2.

Справедливы следующие свойства дисперсии случайной величины:

1. Дисперсия постоянной величины равна нулю: D(C)=0;

2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат, т.е. D(k∙X)=k2∙D(X);

3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий, т.е. D(X+Y)=D(X)+D(Y);

4. Дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: D(X)=M(X2)-[M(X)]2;

5. Для непрерывной случайной величины справедлива формула: D(X) = x²f(x)dx - M²[x]

1. D(C) = 0

2. D(K*X) = K²*D(X)

3. D(X+Y) = D(X) + D(Y)

4. D(X) = M(X²) - [M(X)]²

5. D(X) = x²f(x)dx - M²[x]

33) Понятие моды, медианы, начального и центрального моментов.

Модой M_x(M₀(x)) случайной величины называется ее наибольшая вероятность значения.

Если дан закон распределения дисперсии случайной величины, то мода M_x – это то значение Х, которое встречается в данной серии опытов чаще всего(наибольшая вероятность).

Если случайная величина имеет плотность вероятности, то M_x – это центр того, элементарного интервала, для которого отношение частоты попадания в этот интервал к его длине, достигает максимума.

Медианой X_m(Me(X))непрерывной случайной величиной Xназывается такое ее значение, для которого P(X<x_m) = P(X>x_m)=½

Начальным моментом k-го порядка случайной величины называется математическое ожидание k-ой степени этой случайной величины. Ʋ_k = M[X^k]

Центральным моментом k-го порядка случайной величины х называется математическое ожидание степени µ_k = M[X-M(X)]^k

34) Биномиальный закон распределения и его характеристики, пример.

Дискретная случайная величина X имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, k, …, n с вероятностями

P_n(X=k) = 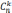p^k(1-p)^n-k

Характеристики:

1. Математическое ожидание случайной величины X, имеющей биномиальный закон распределения, равно M(X)=np;

2. Дисперсия случайной величины X, имеющей биномиальный закон распределения, равна D(X)=np(1-p);

3. Среднее квадратичное отклонение случайной величины X, имеющей биномиальное распределение, равно σ_x=

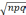
1. M(X) = np

2 .D(X) = np(1-p)

3.σ_x=

Пример:

В магазине поступила обувь с 2ух фабрик в отношении 2 к 3. Куплено 4 пары обуви. Найдите закон распределения купленных пар обуви, изготовленных на 1ой фабрике.

Решение:

Х - кол-во пар обуви, изготовленных 1ой фабрикой, среди купленных 4 пар.

p= =0,4 q=0,6 n=4

xi	0	1	2	3	4
pi	0,1296	0,3456	0,3456	0,1536	0,0256

p₀= *(0,4)⁰*(0,6)⁴=0,1296

M[X]=4*0,4=1,6 D[X]=4*0,4*0,6=0,96 σ=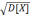 = ≈0,98