24) Функция распределения и её свойства.

Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.

Функция распределения обладает следующими свойствами:      1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.      2. Функции распределения есть неубывающая функция.      3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:       Р(а < X < b) = F(b) – F(а).                                          (2.1)      4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то       F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b.      5.      Справедливы следующие предельные отношения:       .      Для дискретной случайной величины Х, которая может принимать значения х₁, х₂, …,х_n, функция распределения имеет вид      

25) Дискретные случайный величины.

• Случайная величина называется дискретной, если множество ее значений {x₁, x₂, …, x_n} счетно, т.е. можно «пронумеровать».

• Дискретную случайную величину можно задать с помощью таблицы:

Это закон распределения случайной величины.

Геометрическое распределение.

Производится ряд независимых опытов, в каждом из которых с одной и той же вероятностью наступает событие А

Биномиальное распределение.

Пусть производится определенное число n независимых опытов. В каждом из них с одной и той же вероятностью р может наступить некоторое событие А.

Распределение Пуассона.

Пусть производится определенное число n независимых опытов. В каждом из них с одной и той же вероятностью р может наступить некоторое событие А.

Где р_k=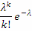 (k=0, 1, 2,…).

26) Дискретные случайные величины. Таблицы и многоугольник распределения. Особенности функции распределения дискретной случайной величины, примеры.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.

Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения).

Рассмотрим случайную величину X, которая принимает значения x₁, x₂, x₃ ... x_n с некоторой вероятностью p_i, где i = 1.. n. Сумма вероятностей p_i равна 1.

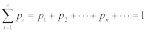
Таблица соответствия значений случайной величины и их вероятностей вида

x1	x2	x3	...	xn	...
p1	p2	p3		pn

называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины.

Графическое представление этой таблицы называется многоугольником распределения.  По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.