17) Схема Бернулли.

Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают 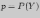, а непоявления (неудачи) его 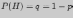. Я. Бернулли установил, что вероятность ровно 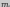успехов в серии из повторных независимых испытаний вычисляется по следующей формуле:

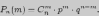
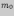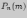То значение , при котором число является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию

np - q m np+ p,

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из событий с вероятностью 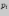( . Вероятность появления 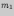раз первого события и - второго и -го находится по формуле

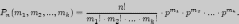
При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

18) Теорема Бернулли и формула Бернулли.

1) Проводятся опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью (или не произойти — «неудача» — 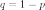). Задача — найти вероятность получения ровно 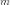успехов в опыте.

Решение:

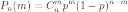
2) Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

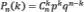
где C_n^k — число сочетаний, q = 1 − p.

Количество успехов — величина случайная, которая имеет распределение Бернулли.

20) Локальная теорема Муавра-Лупласа.

Теорема - Если при каждом из n независимых испытаний вероятность появления некоторого случайного события X равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Если npq > 10 то используется локальная теорема Муавра-Лапласа

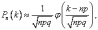Ф – функция Гаусса, которую можно найти по таблице.

Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Решение. По условию 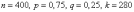 , откуда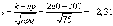

По таблицам найдем  .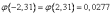

Искомая вероятность равна: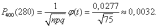 

21) Интегральная теорема Муавра-Лапласа.

Если npq > 10 то используется Интегральная теорема Муавра-Лапласа

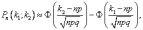 где 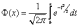 Ф смотреть по таблице.

Так же стоит отметить свойство этой функции

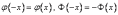
22) Предельная теорема Пуассона. Приближение формулы Пуассона.

Если npq < 10 то применяется теорема Пуассона.

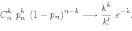
Эта формула используется вместо , 

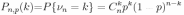Чтобы облегчить себе вычисления.

23) Понятие случайной величины. Закон распределения случайной величины.

Среди задач по теории вероятностей много таких, в которых исход опыта выражается конкретным числом. Примеры: а) при опыте, состоящем в бросании трех монет, частота выпадения герба задается множеством значений {0; 0,(3); 0,(6); 1}, любое из которых может наступить;

• Случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, заранее неизвестно, какое именно (это зависит от случая).

• Множество значений функции f(w) называется множеством значений случайной величины X.

Закон распределения случайной величины.

• Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

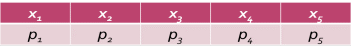
Здесь x_i – возможные значения случайной величины, а p_i – их вероятности (i=1, 2, 3, 4, 5), причем p₁+p₂+p₃+p₄+p₅=1.

• Если случайная величина имеет некий закон распределения, то говорят, что она распределена по этому закону.

 Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.      При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.