10) Теорема о вероятности суммы нескольких событий.

Сумма нескольких событий называется событием, состоящее в наступлении хотя бы одного из данных событий.

Если события совместные, то их сумма – наступление одного события, или наступление второго, или наступление обоих событий вместе.

Если событие несовместные, то их сумма – наступление одного из событий.

11) Аксиоматика вероятностей пространства. Аксиомы событий.

Случайным событием называют любой факт, который может произойти или не произойти.

Событие является элементарным если в результате опыта происходит одно и только одно из них.

12) Аксиоматика вероятностей пространства. Аксиомы вероятностей.

Каждому событию А (А є S) поставлено в соответствие неотрицательное число P(A), называемое вероятностью события А.

13) Условная вероятность. Теорема о вероятности произведения двух событий.

Пусть А и В – два случайных события по отношению к некоторому опыту ơ, причем P(B) ≠ 0. Число P(AB) / P(B) называется вероятностью события А при условии, что наступило событие В, или просто условной вероятностью события А. Вероятностью события А при условии В обозначается P(A/B). Тогда P(A/B) = P(AB) / P(B)

(Теорема 3.3) Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло P(AB) = P(A/B) * P(B).

14) Независимость событий. Теорема о вероятности произведения двух независимых событий.

Событие А называется независимым от события В, если его вероятность не меняется от того, произошло событие В или нет, т.е. P(A/B) = P(A).

Таким образом , А не зависит от события В, если наступление В не оказывает влияния на вероятность А.

(Теорема 3.4) Если событие А не зависит от события В, то справедливо равенство:

P(AB) = P(A) * P(B)

(Теорема 3.4)’ Если выполняется равенство P(AB) = P(A) * P(B) и P(B) ≠ 0, то событие А не зависит от события В.

15) Формула полной вероятности

Событ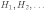ия , образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события могут быть сравнительно просто вычислены (вероятность событию произойти при выполнении «гипотезы» 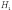) и собственно (вероятность выполнения «гипотезы» ).

(Теорема 3.7) Вероятность события А равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятность самих гипотез :

Р(А) = Р(А/Н1)*Р(Н1) + Р(А/Н2)*Р(Н2) +… + Р(А/Нn)*Р(Нn)

Доказательство: По условию события, А может произойти лишь с одной из гипотез Н1, Н2… Нn. Значит, справедливо равенство: А = АН1 + АН2 + … + АНn. Применяя Th сложения, находим вероятности Р(А) = Р(АН1) + Р(АН2) + … + Р(АНn). А т.к. по Th произведения каждое слагаемое в сумме можно заменить так: Р(АН1) = Р(А/Н1)*Р(Н1)

16) Формула Байеса

Пусть его событие А, которое может наступить лишь вместе с одной из попарно несовместных гипотез Н1, Н2… Нn. Пусть опыт произведен, и событие А наступило, но нельзя сказать какое из событий Н1, Н2… Нn имело место при этом в проделанном опыте.

Р(Н1/А), Р(Н2/А)… Р(Нn/А)

(Теорема 3.8 Формула Байеса)

Справедливо равенство:

Р(Н1/А) = (Р(А/Н1)*Р(Н1)) / (Р(А/Н1)*Р(Н1) + Р(А/Н2)*Р(Н2) +… + Р(А/Нn)*Р(Нn))

Доказательство: Для каждой Н по теореме произведения вероятностей, имеем равенство Р(АН1) = Р(А/Н1)*Р(Н1), аналогично Р(Н1А) = Р(Н1/А)*Р(А). Т.к. АН1=Н1А, то вероятностей можно приравнять, т.е. Р(Н1/А) = (Р(А/Н1)*Р(Н1)) / Р(А), заменив в знаменателе Р(А) на полную вероятность по Th 3.7.