41) Вариационный ряд, таблица частот, гистограмма.

Вариационный ряд: Пусть изучается некоторая случайная величина X. В результате n опытов она приняла значения x1, x2, …, xn. Эту совокупность называют статистическим рядом. Число опытов n называется объемом выборки. Если число n достаточно велико, то значения x1, x2, …, xn удобно помещать в таблицу, которую называют таблицей распределения данных. Среди чисел x1, x2, …, xn выбирают все различные и располагают в порядке возрастания: α1, α2, …αm, причем α1<α2< …<αm. Такой ряд называют вариационным.

Вариационный ряд называется дискретным, если любые его значения отличаются на постоянную величину.

Вариационный ряд называется непрерывным, если любые его значения отличаются друг от друга на сколь угодно малую величину.

Далее составляется эмпирический закон распределения, который может быть задан в виде таблицы частот или в виде интервальной таблицы частот.

Если случайная величина X дискретная, то для нее составляется таблица частот, в которой в первой строке вписаны значения вариационного ряда α1, α2, …αm, а во второй их частоты, т.е. значения μi = ki/n, где ki – число опытов, в которых наступило событие X=αi, n – число всех опытов.

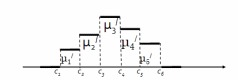
Если случайная величина X непрерывная, то для нее составляют интервальную таблицу частот. В ней в первой строке стоят интервалы (ci , ci+1) (весь диапазон изменения случайной величины разбит на эти интервалы), а во второй строке стоят частоты попадания значений случайной величины в i-тый интервал, т.е. μi '= ki’ / n, где ki’ - количество чисел статистического ряда, приходящаяся на i-тый интервал.

Интервальная таблица частот часто изображается в виде гистограммы – ступенчатой фигуры, у которой основанием является интервал (ci, ci+1), а площадь ступеньки равна μi’.

42) Меры центральной тенденции (средняя арифметическая, мода, медиана, размах, дисперсия) ряда данных.

Рассматривая методы математической статистики, применяемые для обработки данных тестовых исследований, можно выделить группу методов которые могут описывать те или иные меры центральной тенденции. Такие меры указывают наиболее типичный результат, характеризующий выполнение теста всей группой.

Самая известная из таких мер - среднеарифметическое значение (М).

Среднеарифметическое (или выборочное среднее) значение представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута исследованию (выборка испытуемых). Сравнивая среднее значение двух или нескольких групп, мы можем судить об относительной степени развития у людей, составляющих эти группы, оцениваемого качества.

Среднеарифметическое определяется по следующей формуле:

М =

где М - среднеарифметическое значение

n - количество испытуемых

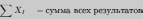
Другой мерой центральной тенденции является мода (Мо) - наиболее часто встречающийся результат. В интервальном частотном распределении мода определяется как середина интервала, для которого частота максимальна.

Третья мера центральной тенденции - медиана (Ме), - результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания. Справа и слева от медианы (Ме) в упорядоченном ряду остается по одинаковому количеству данных (50% и 50%). Если ряд включает в себя четное количество признаков, то медианой (Ме) будет среднее, взятое как полусумма двух центральных значений ряда.

Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных. Дисперсия определяется по следующей формуле:

где 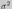- дисперсия

- выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются

n - объем выборки