1) Перебор вариантов, дерево вариантов, примеры.

Если нужных комбинаций не слишком много, то все их можно перечислить, или, как говорят, перебрать все возможности. В этом и состоит метод перебора вариантов.

Пример: Если из цифр 1,5,9 следует составить трёхзначное число без повторяющихся цифр, то все возможные варианты нетрудно выписать. Это 159, 195, 519, 591,915 и 951. Значит, всего можно составить 6 таких чисел.

Один из наиболее известных способов сделать процесс перебора вариантов наглядным заключается в составлении дерева вариантов. На его первом шаге изображают все исходы первого испытания (опыта, эксперимента). Затем в виде веток от каждого исхода изображают все возможные исходы второго испытания и т.д.

Пример: Сколько двухзначных чисел можно составить из цифр

1,4,7?

2) Комбинаторное правило суммы, правило произведения. Перестановки.

ПРАВИЛО СУММЫ

Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (m+n) способами.  При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В.  Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n - k) способов выбора, где k—число совпадений.

Правило произведения

Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать nспособами, то выбор пары (А,В) в указанном порядке можно осуществить mn способами.

При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

Теорема. (перестановок) n различных элементов можно расставить по одному на n различных мест ровно 1*2*3*…(n-2)*(n-1)*n способами.

P_n – число перестановок n элементов. P_n= n!

3) Размещения и сочетания без повторений.

Размещением (без повторений) конечного множества Х, состоящего из k элементов, в конечном множестве Y, состоящем из n элементов, называют любое инъективное отображение из X в Y.

A^k_n - число всех размещений k-элементного множества в n-элементном множестве.(размещения)

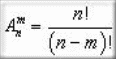
Сочетание – число всех выборов k элементов из n данных элементов без учёта их порядка.

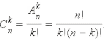
4) Бином Ньютона. Треугольник Паскаля. Основные свойства биномиальных коэффициентов.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) ⁿ  при положительном целом  n  в виде многочлена:

            

Заметим, что сумма показателей степеней для  a  и  b  постоянна и равна n.

Пример  1 .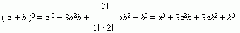 

Числа      называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

Первая строка в этой таблице содержит биномиальные коэффициенты для  n = 1;  вторая - для  n = 2;  третья - для   n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )⁷ , 

мы можем получить результат моментально, используя таблицу:

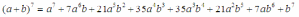
Свойства биномиальных коэффициентов.                                                                                                

 1.  Сумма коэффициентов разложения ( a + b ) ⁿ  равна  2 ⁿ .

Для доказательства достаточно положить  a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

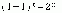
2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

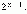
Для доказательства воспользуемся биномом:   Здесь чётные члены имеют знак  « + » , а нечётные - «  ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов   равны между собой, поэтому каждая из них равна: