11. Графы. Реализация представления структуры графа. Списочное и матричное представление графов. (http://school29.Smoladmin.Ru/arbuzov/vvedenie.Html)

В нынешнее время теория графов – один из новейших разделов дискретной математики. Эта наука тесно связана с информатикой, программированием и многими другими сферами научной и бытовой жизни. В виде графов мы часто видим оформление параграфов в учебниках, различные структуры, описание трубопровода, линий высоковольтных передач и многое другое. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

	Итак, граф - это множество точек (вершин, объектов) и соединяющих их путей (линий, дуг, рёбер). Абсолютно неважно, какой вид имеют эти линии, и как точки расположены в пространстве. Идея графа — это набор каких-то объектов, с описанными связями между ними. В самом простом случае связь может быть, а может не быть. В нашем случае вершинами являются части суши города, а ребрами – мосты. На рисунках приведено изображение мостов в виде карты (слева) и в виде графа (справа).
В строгом определении графом называется такая пара множеств G=(V,E), где V (множество вершин графа) есть подмножество любого счётного множества, а E (множество ребер графа, или множество неупорядоченных и упорядоченных пар вершин) — подмножество V×V. На рисунке слева приведен пример графа с шестью вершинами и семью ребрами.

Теперь сформулируем основные понятия, которыми мы будем «оперировать» в данном пособии.

Граф может быть ориентированным и неориентированным. В ориентированном графе пути (дуги) имеют направление, а в неориентированном - не имеют. Все приведенные выше примеры графов – неориентированные графы. Неориентированное ребро можно представить как две разнонаправленные дуги между двумя вершинами. Пути в неориентированном графе называются рёбрами.

Путь в графе или орграфе - это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины A в вершину B начинается в A и проходит по набору ребер до тех пор, пока не будет достигнута вершина B.

Связный граф – это такой граф, что между любыми парами вершин есть хоть один путь.

Взвешенным называется такой граф, для каждого ребра (дуги) которого определена некоторая функция. А эта функция называется весовой. Иначе говоря, к каждому ребру «привязан» вес - фиксированное число или результат какой-то функции. Чаще всего встречается первый вариант.

Цикл – замкнутый путь в графе, в котором все вершины, кроме начальной и конечной попарно различны. Дерево – граф без циклов. Им, например, является структура содержания книги.

Петлей называется дуга, ведущая из вершины в нее же.

Рассмотрим пример ориентированного взвешенного графа.

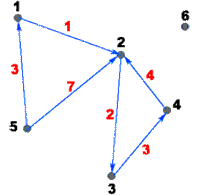На рисунке точками обозначены вершины графа, стрелками - дуги, чёрные числа - номера вершин графа, а красные - веса дуг. Вес дуги можно представить также как стоимость. Т.е. например: дан граф, нужно дойти от вершины i до вершины j, заплатив минимальное количество денег или потратив наименьшее количество времени. Пусть в нашем графе, который представлен на рисунке, нам нужно пройти из вершины 5 в вершину 2, а вес дуг - стоимость прохода по данному ребру (или время прохода по нему). В данном примере очевидно, что выгоднее пройти через вершину 1 и только потом прийти в вершину 2, так мы заплатим всего 4 единицы денег, иначе, если пойти напрямую, мы заплатим целых 7 единиц.

Петлей называется дуга, ведущая из вершины в нее же. Четность вершины определяется количеством исходящих из нее ребер: если оно четно, что и вершина четна, и наоборот.

Матрица смежности

Один из самых распространённых способов хранения графа - матрица смежности. Она представляет собой двумерный массив. Если в клетке i, j (i – строка, j - столбец) установлено значение пусто (как правило, это очень большая величина или величина, которой заведомо не может равняться вес ребра), то дуги, начинающейся в вершине i и кончающейся в вершине j, нет. Иначе дуга есть. Если она есть, то в соответствующую ячейку записывают ее вес. Если граф не взвешенный, то вес дуги считается равным единице. Составим матрицу смежности для нашего графа:

	1	2	3	4	5	6
1	0	1	0	0	0	0
2	0	0	2	0	0	0
3	0	0	0	3	0	0
4	0	4	0	0	0	0
5	3	7	0	0	0	0
6	0	0	0	0	0	0

Если нам дан неориентированный граф, то ребро можно заменить двумя дугами, т.е. если у нас есть ребро (1,3), то мы можем заменить его на дуги (1,3) и (3,1) - так мы сможем пройти в любом направлении в любое время.

Как вы уже заметили, в матрице смежности нам часто нужно хранить большое количество нулей. Например, в нашей матрице "нужных" значений только 6, а остальные 30 - нули, не представляющие для нас почти никакой нужной информации.

Для представления графа матрицей смежности нужно V² (где V - количество вершин) ячеек. Если граф почти полный, т.е. Е сопоставимо V² (где Е - количество дуг), этот способ хранения графа наиболее выгоден, т.к. его очень просто реализовывать и память будет заполнена "нужными" значениями.

Но если это условие не выполняется, например, вершин до 10000 и ребер до 1000, то нам понадобиться ≈2 * 100000000 / 1024² Мбайт памяти (по 2 байта на ячейку), что примерно равно 190 Мбайт, памяти. А на олимпиадах, как правило, ограничении на ее использование составляет 64 Мбайт. Значит, этот метод не годиться.

Кроме большого количества требуемой памяти и медленной работы на разреженных графах (графах, у которых E << V²) у матрицы смежности есть ещё один важный недостаток. Иногда в задачах нужно выводить не номера вершин, а номера дуг (рёбер) на вводе. Хранить эти номера матрица смежности «не умеет». Нужно реализовывать восстановление номера дуги (ребра) как-то иначе, а это совсем неудобно.

Приведем расчеты временной сложности хранения графа матрицей смежности:

Операция Временная сложность

Проверка смежности вершин x и y О(1)

Перечисление всех вершин смежных с x О(V)

Определение веса ребра (x, y) О(1)

Перечисление всех ребер (x, y) О(V²)

Список дуг

Следующий тип хранения графа в памяти компьютера - список дуг. Чаще всего это двумерный массив размером 3*E, в первой строке которого хранится информация, из какой вершины начинается дуга, во второй - в какой кончается, а в третьей строке - вес дуги. Опять же разберёмся на примере (все тот же граф):

1 2 3 4 5 6

1 1 2 3 4 5 5

2 2 3 4 2 1 2

3 1 2 3 4 3 7

Мы чётко видим, что почти вся таблица заполнена "нужными" значениями, а не нулями. Это уже хорошо, значит, память экономится.

Приведем расчеты временной сложности хранения графа списком дуг:

Операция Временная сложность

Проверка смежности вершин x и y О(E)

Перечисление всех вершин смежных с x О(E)

Определение веса ребра (x, y) О(E)

Перечисление всех ребер (x, y) О(E)

Поиск i-ой дуги О(1)

Как видно, этот способ, в отличие от матрицы смежности, хранит информацию о номере дуги. Также ясно, что этот способ нам выгоден, если чаще всего нам нужно будет узнать что-то (вес, вершины начала или конца) о i-ой дуге. Однако, такие задачи в практическом программировании встречаются довольно редко.

Если в предыдущих представлениях одно ребро мы заменяли двумя дугами, то список дуг может хранить или дуги или рёбра (в зависимости от реализации). Это довольно удобно и может требовать в 2 раза меньше памяти.

Списки смежных вершин

Данный метод хранения графа наиболее часто используется при решении задач с большими ограничениями по памяти и по времени (например, 2 сек и 64 Мбайт памяти на ограничения V< 10000, E < 1000 – случай разреженного графа). Его суть заключается в том, чтобы для каждой вершины Т хранить номера вершин, в которые можно попасть из Т, и вес соответствующих ребер (дуг). Для этого необходимо реализовать такую структуру данных, как список. В языках высокого уровня, таких, как С++ и Java, они уже реализованы. Далее нужно реализовать структуру данных (struct в C++ и record в Pascal) – запись с полями «вершина» и «вес». После этого заводим массив списков с V ячейками (количество вершин) и к каждой ячейке «привязываем» список созданного нами типа (структуры).

Приведем листинг на языке С++:

….

#include <list>

….

….

struct ToLength

{

int to; //номер вершины

int length;//вес ребра

ToLength() //пример первичной инициализации (зависит от постановки задачи)

{

to = -1;

length = 0;

}

ToLength(int t, int l) // инициализация входными числами

{

to = t;

length = l;

}

};

int main()

{

…

list<ToLength> mass[v];

…

return 0;

}

После этого каждый элемент mass[i] является списком типа ToLongth динамической длины (в зависимости от кол-ва ребер, исходящих из данной вершины).

Эта схема поможет воспринять метод:

mass[0] : . . . . . . . . . . .

mass[1] : . . . . . . . . . . . . . . . .

…..

mass[v] : . . . . .

где «….» – это длина списка, количество вершин, исходящих из i-ой вершины графа.

Для данного примера массив списков будет выглядеть так (в скобках указаны элементы структуры):

Номер ячейки : элементы списка.

1 : (2, 1), (5, 3)

2 : (3, 2)

3 : (4, 3)

4 : (2, 4)

5 : (1, 3), (2, 7)

6 :

Приведем расчеты временной сложности хранения графа списками смежных вершин:

Операция Временная сложность

Проверка смежности вершин x и y О(E)

Перечисление всех вершин смежных с x О(E)

Определение веса ребра (x, y) О(E)

Перечисление всех ребер (x, y) О(E)

Поиск i-ой дуги О(1)

Времена у всех операций, вроде бы, такие же, как и у списка рёбер. Однако, большинство из них реально намного меньше. Например, проверка смежности вершин x и y и перечисление всех вершин смежных с x в списке рёбер гарантированно будет выполнятся О(Е) операций, т.к. нам обязательно нужно пробежать весь список, а в списке смежности мы бежим только по вершинам, смежным с х.

Кроме того, мы экономим колоссальное количество памяти. Подсчитаем примерный объем для максимального ограничения: 2 * (10000 * 1000) / 1024² ≈ 19 Мбайт.

Как видно, это в 10 раз меньше, чем при хранении матрицей смежности, при одинаковых ограничениях. Стоит ещё раз отметить, что, если граф неразреженный, то особой разницы хранения графа нет. Главное, чтобы способ был удобен для выполнения поставленной задачи.

Итак, мы рассмотрели лишь некоторые методы представления графа в памяти компьютера. Существует ещё много способов представления графа в памяти, как статических, так и динамических. Однако не стоит распыляться на все сразу, так как они мало чем могут помочь на олимпиаде по информатике. Все методы, рассмотренные выше, хороши для решения школьных олимпиадных задач, не требуют долгой и сложной реализации, поэтому нужно иметь их на вооружении. Можно сделать выводы, что наиболее оптимальной структурой является массив списков, так как он экономит память и не тратит драгоценное время. Но чтобы им смело пользоваться, надо много потренироваться в его реализации. В главе «Разборы задач» многие решения хранят графы в виде списков смежных вершин. Однако в теоретической чести мы будем разбирать алгоритмы на примерах реализации графа в виде матрицы смежности. Это позволяет проще понимать суть логики алгоритма.