4. Структура данных дерево(не обязательно бинарное). Кодировка в виде списковой структуры. Бинарное дерево поиска, длина ветви, баланс вершины.

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указываются, что рёбра графа не должны быть взвешенными.

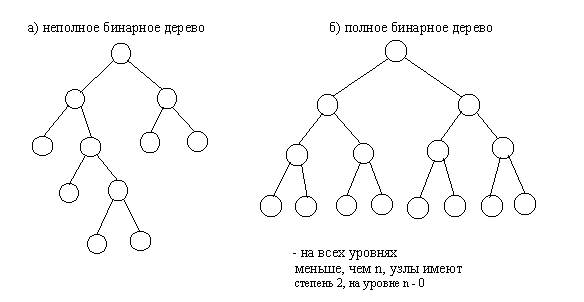
Бинарные деревья классифицируются по нескольким признакам. Введем понятия степени узла и степени дерева. Степенью узла в дереве называется количество дуг, которое из него выходит. Степень дерева равна максимальной степени узла, входящего в дерево. Исходя из определения степени понятно, что степень узла бинарного дерева не превышает числа два. При этом листьями в дереве являются вершины, имеющие степень ноль.

Другим важным признаком структурной классификации бинарных деревьев является строгость бинарного дерева. Строго бинарное дерево состоит только из узлов, имеющих степень два или степень ноль. Нестрого бинарное дерево содержит узлы со степенью равной одному.

5. Операции над бинарными деревьями поиска: вставка, удаление вершины и др. Операции.

Рассматривая действия над деревьями, можно сказать, что для построения дерева необходимо формировать узлы, и, определив предварительно место включения, включать их в дерево. Количество узлов определяется необходимостью. Алгоритм включения должен быть известен и постоянен. Узлы дерева могут быть использованы для хранения какой-либо информации.

Далее необходимо осуществлять поиск заданного узла в дереве. Это можно организовать, например, последовательно обходя узлы дерева, причем каждый узел должен быть просмотрен только один раз.

Может возникнуть задача и уничтожения дерева в тот момент, когда необходимость в нем (в информации, записанной в его элементах) отпадает. В ряде случаев может потребоваться уничтожение поддерева.

Для того, чтобы совокупность узлов образовала дерево, необходимо каким-то образом формировать и использовать связи узлов со своими предками и потомками. Все это очень напоминает действия над элементами списка.

Опять же есть нескольно основных операций над бинарными деревьями.

1. Добавление

2. Удаление

3. Поиск

4. Обход – это дополнительная операция к трем основным, которые мы рассматривали в структурах данных.

Добавление

Добавление элемента в бинарное дерево – операция, которая имеет логарифмическую сложностьпо отношению размеру дерева (logn). Это очень интересная операция, потому что каждый элемент в бинарном дереве имеет определенную позицию. Поэтому сначала надо найти, куда его поставить, а затем и осуществить это.

Поиск

Сейчас пришло время представить операцию поиска в бинарном дереве. Она выглядит как добавление и занимает логарифмическое время (logn). Это относится к хорошо сбалансированному дереву, конечно!

Код в C/C++:

1 2 3 4 5 6 7 8 9

tree *search_tree(const tree *t, item_type i) { if (t == NULL) return NULL; if (t->item == i) return t; if (i < t->item) { return search_tree(t->left, i); } else { return search_tree(t->right, i); } }

Удаление

Удаление элемента из дерева самая трудная операция. Тем не менее она также отнимает logn время. Есть несколько специальных ситуаций, которые должны быть решены:

1. Удаление элемента без детей – просто освобождаем память.

2. Удаление элемента с одним ребенком – смена указателя родителя указывать директно к ребенку удаляемого элемента и освобождение памяти.

3. Удаление элемента с только одним ребенком и это КОРЕНЬ – перемещение ребенка на место корня и освобождение памяти.

4. Удаление элемента с двумя детьми – это самая сложная операция. Самый подходящий способ исполнения это разменять стоимости удаляемого элемента и максимальную стоимость левого поддерева или минимальную правого поддерева (потому что это сохранит характеристики дерева) и тогда удаляем элемент без или с одним ребенком.

Обход дерева

Обход дерева, это процесс обхождения всех узлов и их обрабатывании. Существует три типа обхода бинарного дерева:

1. Inorder – посещение левого поддерева, корня и правого поддерева.

2. Preorder – посещение корня, левого поддерева и правого поддерева.

3. Postorder – посещение левого поддерева, правого поддерева и корня.

6. Алгоритм и программа сортировки со вставкой элемента, их особенности, возможности улучшения.

Сортировка вставками (Insertion Sort) — это простой алгоритм сортировки. Суть его заключается в том что, на каждом шаге алгоритма мы берем один из элементов массива, находим позицию для вставки и вставляем. Стоит отметить что массив из 1-го элемента считается отсортированным.

Словесное описание алгоритма звучит довольно сложно, но на деле это самая простая в реализации сортировка. Каждый из нас, не зависимо от рода деятельности, применял алгоритм сортировки, просто не осознавал это:) Например когда сортировали купюры в кошельке — берем 100 рублей и смотрим — идут 10, 50 и 500 рублёвые купюры. Вот как раз между 50 и 500 и вставляем нашу сотню:) Или приведу пример из всех книжек — игра в карточного «Дурака». Когда мы тянем карту из колоды, смотрим на наши разложенные по возрастанию карты и в зависимости от достоинства вытянутой карты помещаем карту в соответствующее место. Для большей наглядности приведу анимацию из википедии.

Реализация

Прежде чем приступить к реализации определимся с форматом входных данных — для примера это будет массив целочисленных (int) значений. Нумерация элементов массива начинается с 0 и заканчивается n-1. Сам алгоритм реализуем на языке C++. Итак приступим…

Основной цикл алгоритма начинается не с 0-го элемента а с 1-го, потому что элемент до 1-го элемента будет нашей отсортированной последовательностью (помним что массив состоящий из одного элемента является отсортированным) и уже относительно этого элемента с номером 0 мы будем вставлять все остальные. Собственно код:

for(int i=1;i<n;i++) for(int j=i;j>0 && x[j-1]>x[j];j--) // пока j>0 и элемент j-1 > j, x-массив int swap(x[j-1],x[j]); // меняем местами элементы j и j-1

Реализация сортировки очень проста, всего 3 строчки. Функция swap меняет местами элементы x[j-1] и x[j]. Вложенный цикл ищет место для вставки. Рекомендую запомнить этот алгоритм, чтобы в случае необходимости написать сортировку не позориться сортировкой пузырьком:)