
Figure 30 Ist Scenario
x - is a distance between person and painting
h – is a height of the eye level of the person – 150 cm and 200 cm
L – as a height placement of the painting on the wall – 160 cm
l – is a difference between h and L – 10 cm or 40 cm more
Ph – is a size of the painting - 80
θ – viewer’s angle on the painting
β – viewer’s angle on the distance between painting and eye level
α – θ + β, angle from eye level to the highest point of the painting
Figure 30 represents a case when person’s height is 150 cm
Figure 31
f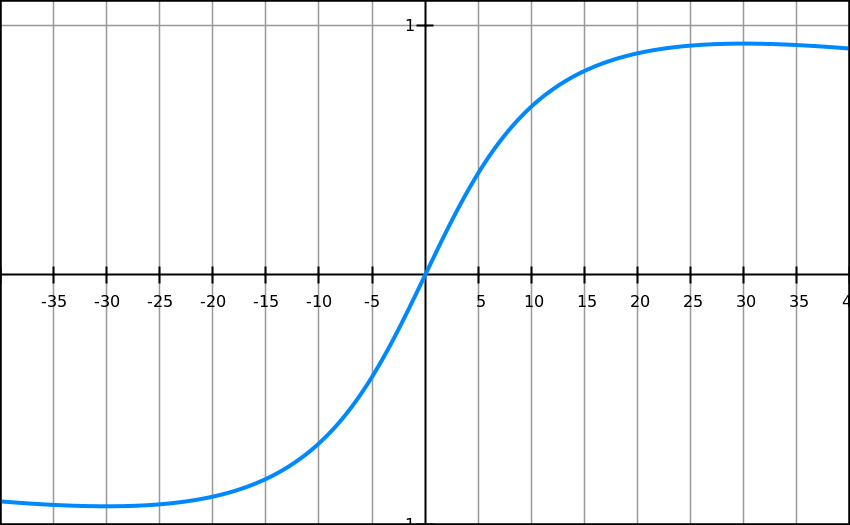 (x)
= Tan-1
(
(x)
= Tan-1
( Tan-1
(
Tan-1
(
f(x) =
Tan-1
(
 Tan-1
(
Tan-1
(
Figure 31 clearly shows that Maximum point is between x=25 and x=35
f
‘(x) =


f
‘(x) =
Figure 32
 x=
-30 and x=30 (figure 32)
x=
-30 and x=30 (figure 32)
We need only positive number as we need maximised value
So when distance from the picture is 30 cm person will see the picture with maximised angle, we will find this angle through already found x value.
θ
= Tan-1
( Tan-1
(
Tan-1
(
θ = 0.9272 Radians
θ
= 0.9272 = 51.5662゚
= 51.5662゚
Figure 33
In this case α is in front of the size of the painting – 80 cm
But other and very important point is that θ triangle has a straight angle but it is now not a full angle of the view
Figure 34
α
= 2Tan-1
(

 ormula
for finding θ will
be: (Figure 34)
ormula
for finding θ will
be: (Figure 34)
θ = Tan-1 (
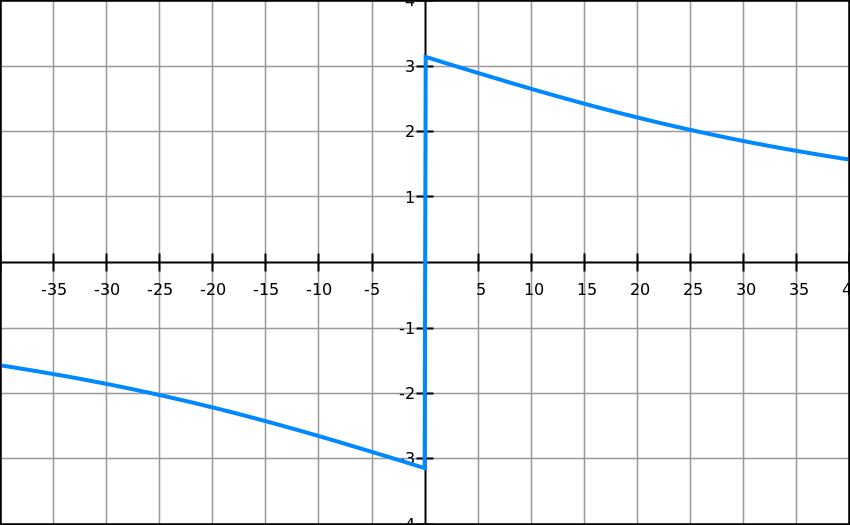
Differentiated formula will be
θ’
=
β is a straight triangle as well and its opposite side is 40 cm
it is reasonable to state that α will be 2θ
α = 2 Tan-1 (
α’=
α’
=
Figure 35
 t
α’
=0 equation has an
error
t
α’
=0 equation has an
error
x |
α’ = |
-1 |
0.000083 |
0 |
undefined |
1 |
0.000083 |
At x=1 θ will be:
α
= 2Tan-1
(
α = 177゚
At the case when person’s eye level height is 150 optimised distance from the painting is 30 cm and angle is 51.5゚; for the case when person’s eye level is at some point at the painting maximised angle should be 180゚, but it is not impossible so the least distance for the viewer can be 1 cm, at one cm the viewing and is 177゚.
Figure 36
IInd Scenario
x - is a distance between person and painting
h – is a height of the eye level of the person – 150 cm and 200 cm
L – as a height placement of the painting on the wall – 130 cm
Ph – is a size of the painting - 110
θ – viewers angle on the painting α + β
β – viewers angle on the distance between height placement of painting and eye level
α –angle from eye level to the highest point of the painting (figure 36)
An equation for the scenario two where eye level is on the painting will be:
θ= α + β
Opposite side for β will be h – L
For the case when person height is 150 opposite side for the β is:
150-130=20 cm
Figure 37
1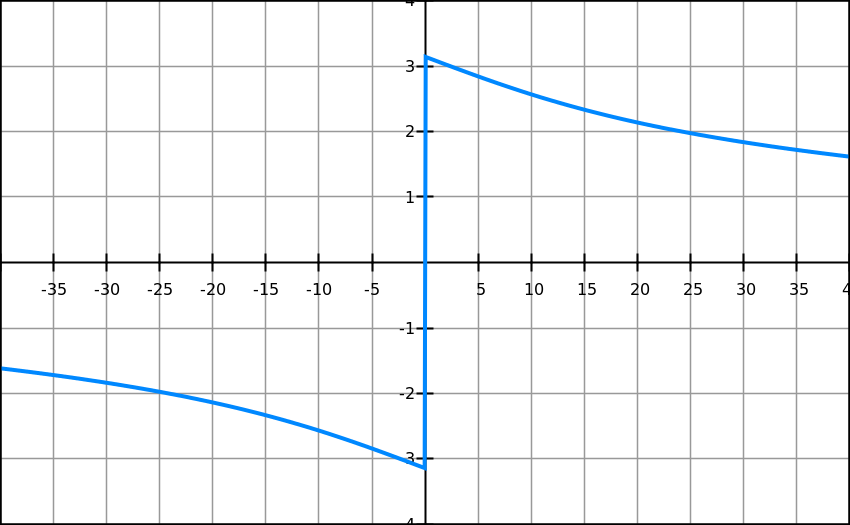 10-20=90
cm
10-20=90
cm
α=
Tan-1
(
β=
Tan-1
(
θ=
Tan-1
(
Figure 37 shows that the clearest viewing angle for the painting will be 180゚as in case 2 at the 1st scenario.
Figure 38
Opposite side for β:
200-130=70 cm
Opposite side for α:
110-70=40 cm
α=
Tan-1
(
β=
Tan-1
(
x |
θ
‘(x) =
|
-1 |
6502 |
0 |
undefined |
1 |
6502 |
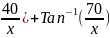
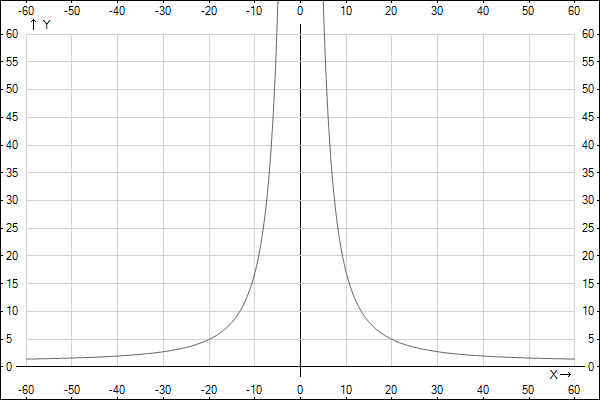
Table for the derived function provides the evidence that maximum angle for the viewing is 180゚
Figure 39
x - is a distance between person and painting
h – is a height of the eye level of the person – 150 cm
L – as a height placement of the painting on the wall – 150 cm
Figure 40 h
– is a size of the painting - 60
h
– is a size of the painting - 60
θ – viewers angle on the painting
θ
= Tan-1
( )
)
θ
= Tan-1
( )
)
θ‘ =
The graph is the same as cases when eye level is on the painting, this means that optimised angle for this case is 180゚but it is not possible in real life
At the case when person’s eye level height is 150 optimised distance from the painting is 30 cm and angle is 51.5゚; for the case when person’s eye level is at some point at the painting maximised angle should be 180゚, but it is not impossible so the least distance for the viewer can be 1 cm, at one cm the viewing and is 177゚, for the cases wen person’s look goes straight at the painting optimised angle for it is 180゚ at zero distance.
At the cases when viewing person is lower them a height of the placement for 10 cm and when eye level is looking straight at a painting optimised distance for people with height from 150 cm to 200 cm is from 1 cm to 30 cm, the angle will be from 51.5゚ to 177゚
Investigated data gives evidence that mathematical optimisation method is not reasonable for real-world situation due to impossible results as zero distance. For the museum keepers it is not advisable to let people approach the painting closer than 30 cm, but this distance is just the most optimised for a case when the painting is 80cm and it is 10 higher than eye level. The height of the placement should not be high due to standards, but 152 cm will not be proper for optimisation because average people’s height is 160 and optimised angle will be 180゚ which is not reasonable.


