Functions with combination of features
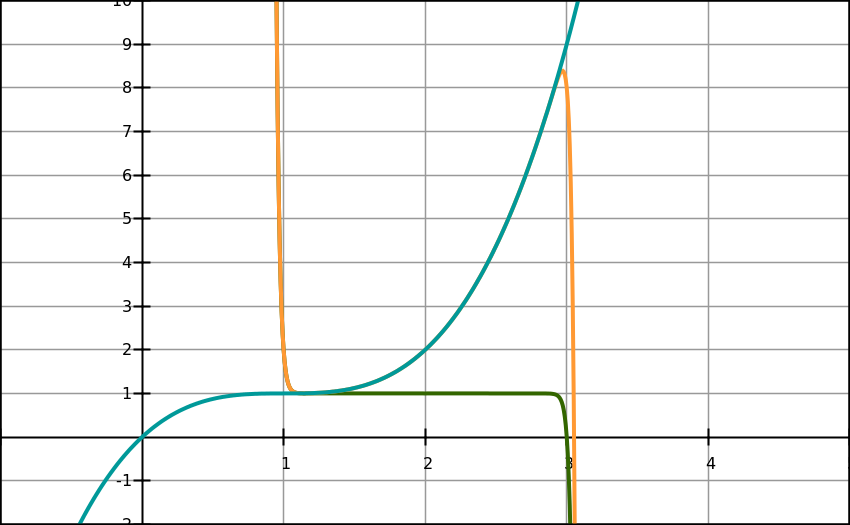
Figure 26
f(x)=
f(x)=
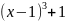
o
get proper curve proper values should be used. To make a curve with
one point of inflection, one maxima and one minima with a shift along
the x-axis, both
and
fractions need to have the same shift, otherwise the curve of the
subtraction of the functions will not have a proper shape (Figure 26)
Figure 27
f(x)=
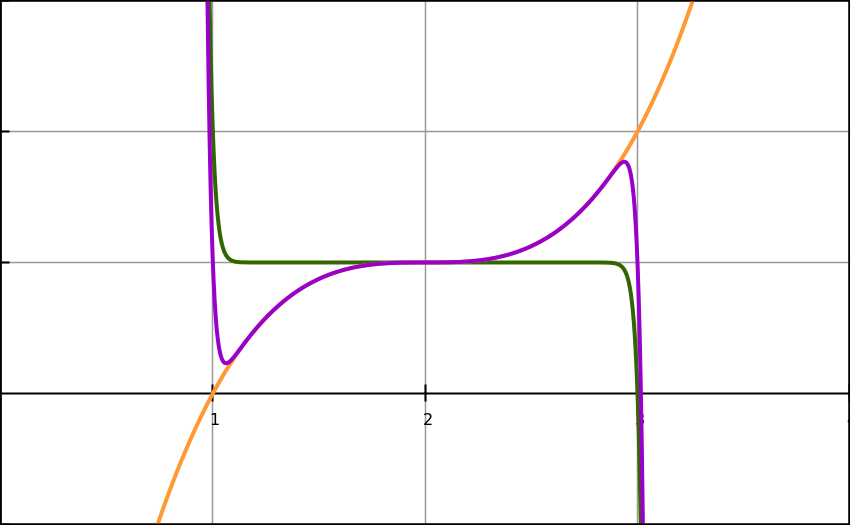(x)=
and f(x)=
functions have different stationary point values, they do not match
so the curve of their sum has no point of inflection when f(x)=
values take f(x)=
values
f(x)=
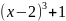
f(x)=
f(x)=
To add a cusp curve to the
f(x)= function the cusp curve should have the same shift along the x-axis because the cusp and the point of inflection should coincide with each other or cusp needs to coincide with any point of the other curve to create a cusp in a new curve
All functions can be modified in different cases, but in the situation when I want to get a cusp, and at least some other clear points I will create a cusp in the middle and use a normal cusp curve f(x)= to clearly outline newly created stationary points.
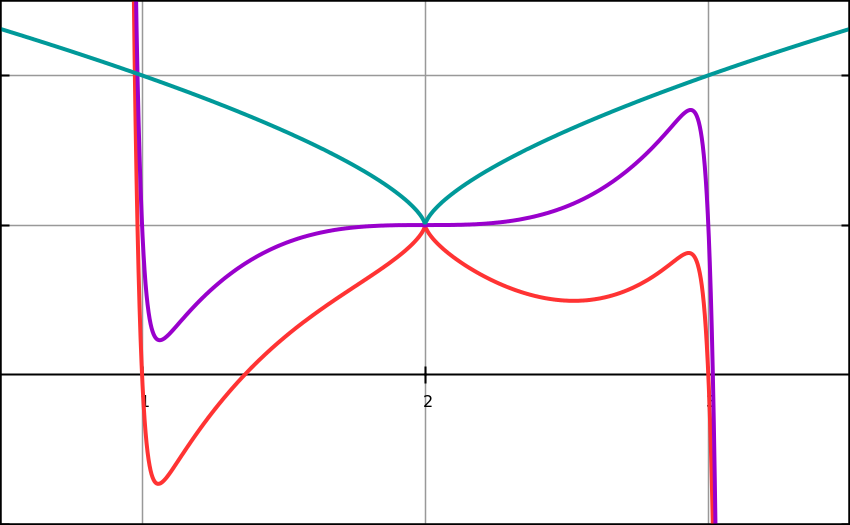
Figure 28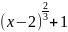
will be combined by subtraction
f(x)=
(x)=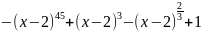
f(x)=
f(x)=
f(x)=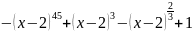
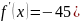
X= 2
X=1.0577
X= 2.2222
X= 2.93149
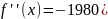
(2)=
- 2/3 (local max)(1.0577)= 147.4243 (local min)
(2.2222)= 0.6665 (local min)
(2.93149)= -88.68889 (local max)
At x=2 the curve has a cusp, and at x=1.0577 (local min), x=2.2222 (local min), x=2.93149 (local max)
(Complex calculations were made at http://www.wolframalpha.com/)
Question 5
Gumnut gallery
This report will investigate the distance viewers should be advised to stand away from a wall on which paintings are hung in order to optimise their viewing angle
Figure 29
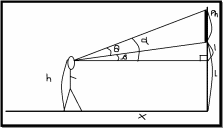Figure
29 has a sketch of few patterns:
x - is a distance between person and painting
h – is a height of the eye level of the person
L – as a height placement of the painting on the wall
l – is a difference between h and L
Ph – is a size of the painting
θ – viewers angle on the painting
β – viewers angle on the distance between painting and eye level
α – θ + β, angle from eye level to the highest point of the painting
As it is clearly provided on the figure 29 a triangle with α angle has a straight angle, triangle with β angle has a straight angle as well, the wanted angle which should be maximised is θ, but this angle is a part of the triangle which does not have a straight angle. A straights angle is to find a formula for unknown angle through triangles sides – opposite, adjacent and hypotenuse.
Sin
=
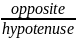Cos
=
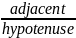Tan
=
So to find α we will need two sides: size of the painting + is a difference between h and L – opposite side and distance between person and painting – adjacent side which is x and should be found as well. Formula for the α will be:
α
= Tan-1
(
α
= Tan-1
(
Knowing that α is a sum of two smaller triangles we can find θ triangle trough this pattern. As triangle with β angle has a straight angle as well as α triangle We can work through Tan formula to find β
β = Tan-1 (
β
= Tan-1
(
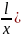
Now it is possible to find θ through α taking β
θ = α – β
θ
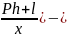= Tan-1
(
Tan-1
(
If to denote θ as f(x) there will be an equation which will help to find maximised x to make a maximised θ
f(x) = Tan-1 ( Tan-1 (
To use an application to optimisation problems and finding maxima of the curve to state a maximised distance for finding maximised angle the investigated equation will need to be differentiated
Differentiate formula for Tan-1(x):
Let y= Tan-1(x)
Where
Then let Tan y = x
Using implicit differentiation and solving for dv/dx
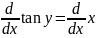
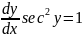
When 1+Tan2 y = sec2 y
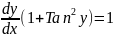
When x = Tan y
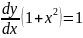
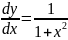
So
Differentiated f(x) = Tan-1 ( Tan-1 ( formula will be
f
‘(x) =
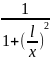
Investigated formula will help to find maximised angle for all cases when h is less then L