
Optimization
of functions
Item
4.2 Extended Modeling & Problem-Solving Task
Authored by: KULESHOVA,
Anastasiia



Queensland Government
Question 1
 functions where a
is a rational number
functions where a
is a rational number

Figure 1
For functions f(x)=x2 and f(x)=x4 gradient functions will be f ’(x)=2x and f ‘(x)=4x3 , and at f(x)=0 both functions have only one answer: x=0. This means that other functions with even numbers will have a minimum at x=0. Functions where a is even have a parabola shape with minimum value at x=0 (see Figure 1 graph)
f(x)=x100
f(x)=x10
f(x)=x4
f(x)=x2

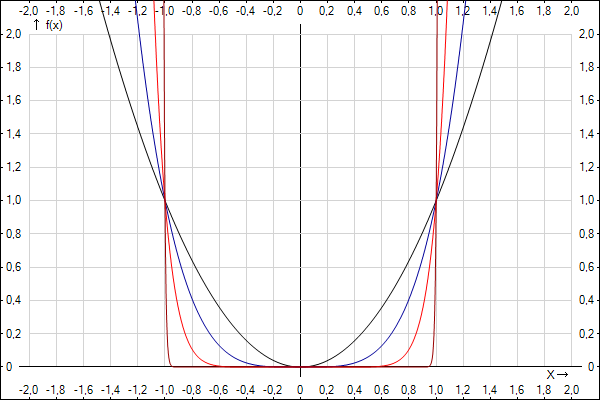
Figure 2
I have
chosen function f(x)=x10
as general shape
function because all positive rational numbers before 10 have smooth
graphs, and all numbers after 10 have similar shape with almost
sharp angles of the graph.

f(x)=x10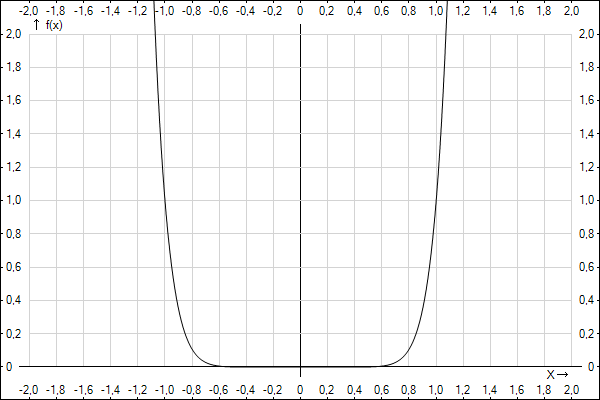
Figure 3
For functions f(x)=x3 and f(x)=x5 gradient functions will be f ’(x)=3x2 and f ’(x)=5x4 , and at f(x)=0 both functions have only one answer: x=0. To find what stationary point it is we need to find second derivative of this functions: f ’’(x)=6x and f ’’(x)=20x3 , f ’’(0)=0 for both functions – so this stationary point is a point of inflection. Similarity of those two functions means that other functions with odd numbers will have a point of inflection too. Functions where a is odd have a cubic parabola shape with minimum value at x=0 (see Figure 3)
f(x)=x101
f(x)=x11
f(x)=x5
f(x)=x3

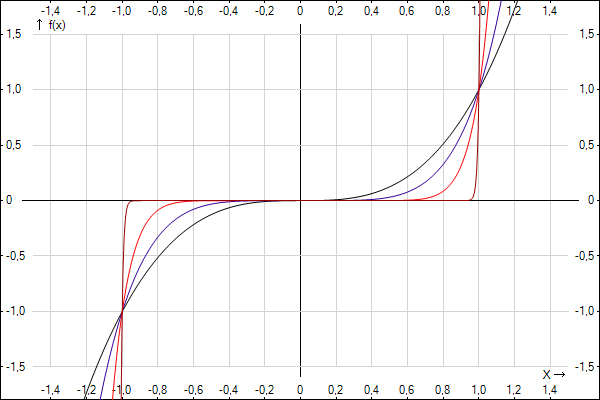
Figure 4
I have
chosen function f(x)=x11
as general shape
function because all positive rational numbers before 11 have smooth
graphs, and all numbers after 11 have similar shape with almost
sharp angles of the graph.
f(x)=x11
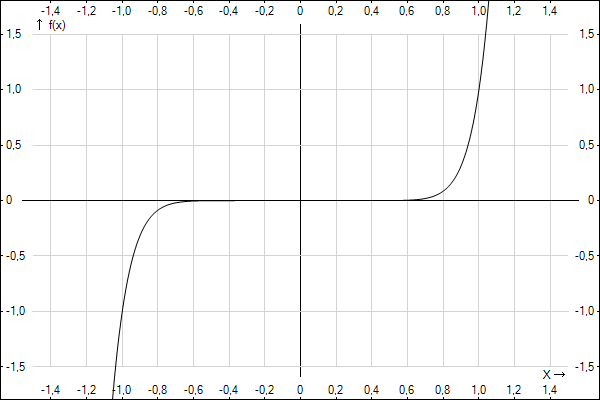
Figure 6
Figure 5
 Functions
f(x)=
Functions
f(x)=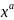 with positive fractional values instead of a
have two general shapes:
with positive fractional values instead of a
have two general shapes:
f(x)=
f(x)=

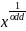
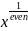
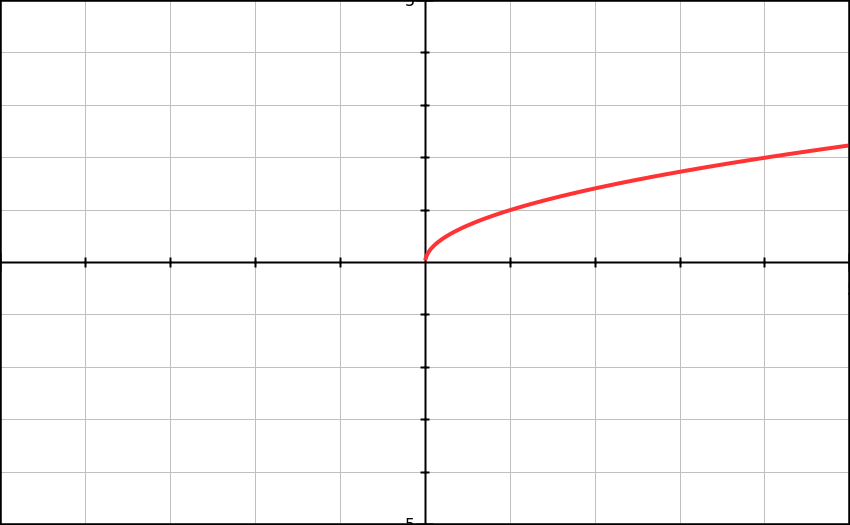
Figure 5 outlines shape for fractional values with even denominator and Figure 6 outlines shape for fractional values with odd denominator.
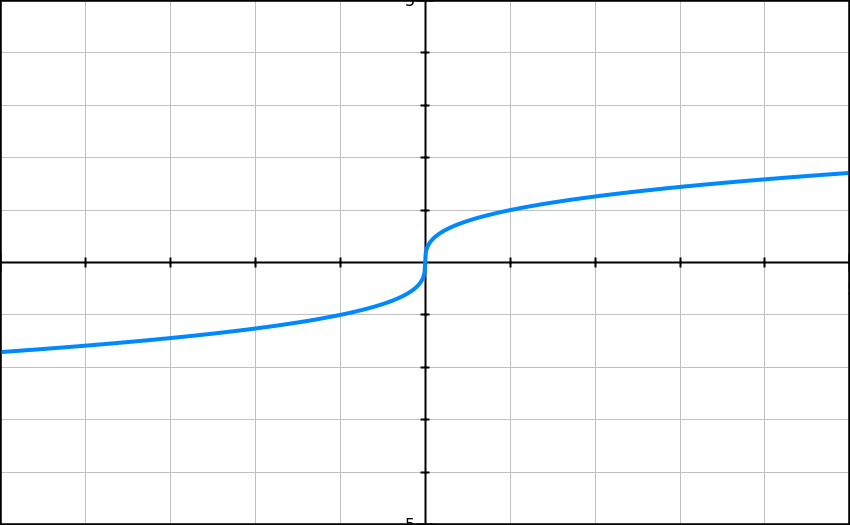
On the assumption of two general shapes for fractional values instead of a it is reasonable to state that all fractional values with odd denominator will be defined for all x (see figure 6).
Referring to general shapes for fractional functions will help to investigate gradient at x=0:
For
f(x)=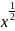
f
’(x)=
 and at x=0 f ’(0)= undefined, so there is no gradient there
and at x=0 f ’(0)= undefined, so there is no gradient there
This will happen with all even dominators at fractional values, the shape of the graph for these values confirms this assumption.
For
f(x)=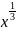
G-calc for f ’(x)= when x=0

Value
of the gradient increases till 933.892 – this is a gradient for f
’(x)= ,
after this number gradient stays the same, before this number
gradient increases from 100.
,
after this number gradient stays the same, before this number
gradient increases from 100.
Two general shapes for function with fractional values instead of a show that none of these functions have minimum at all, so it is impossible to have minimum at x=0 for functions with fractional values with numerator=1 instead of a.
Figure 8
Figure 7
Functions f(x)= with positive fractional values instead of a: for example a=
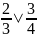 , these fractions have two general shapes (see Figure 7 and Figure
8)
, these fractions have two general shapes (see Figure 7 and Figure
8)
f(x)=
f(x)=
f(x)=
f(x)=
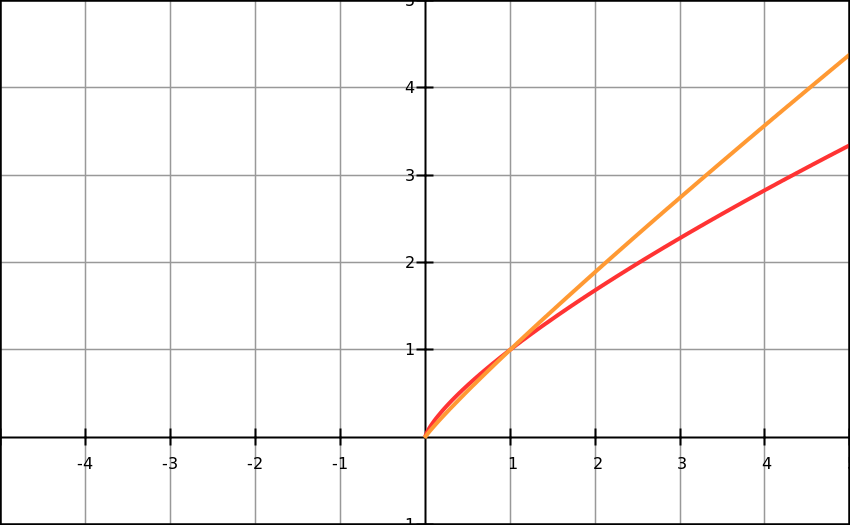
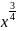

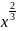
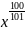
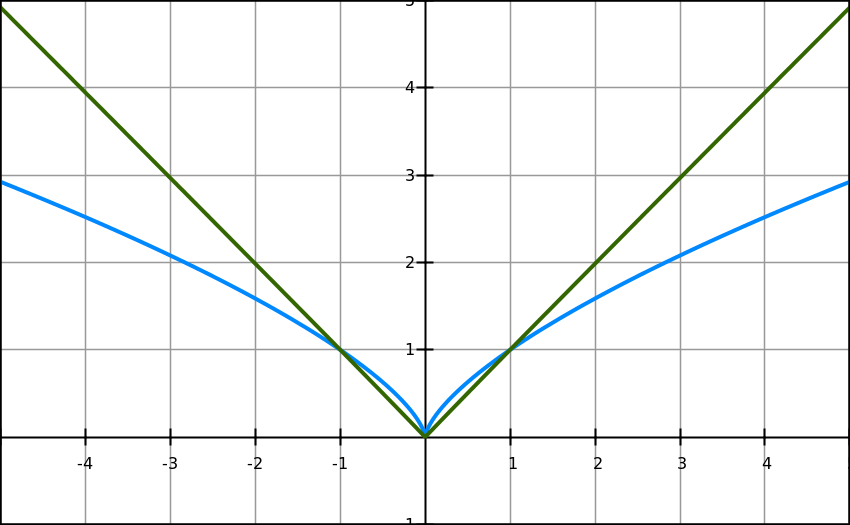
Figure 7 and Figure 8 show consistent pattern that fractions where numerator is even and denominator is odd will have a graph which doubles itself after crossing y-axis. Fractions where numerator is odd and denominator is even will have a graph with only x-positive values.
f(x)=
f(x)=

Index for the radical fraction is odd and this means that domain for this function is [∞;∞]
f(x)=
f(x)=
after
that
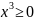
This means that the domain of this function is [0;∞]
x |
f(x)= |
f(x)= |
-2 |
1.6 |
undefined |
-1 |
1 |
undefined |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
1.6 |
1.7 |
Calculus, table and graph evidence confirm that functions f(x)= and f(x)= have different domains.
There are other possible f(x)= with fractional values instead of a:
If values will be negative – graphs of the function will become hyperbolic
Figure 9
f(x)= Derivative
function will be: f ’(x)= When
f ’(x)=0 x=0 When
x=0 f(0)= Stationary
point for f(x)=
function is (0;0)
f(x)=

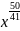

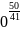 f(0)=0
f(0)=0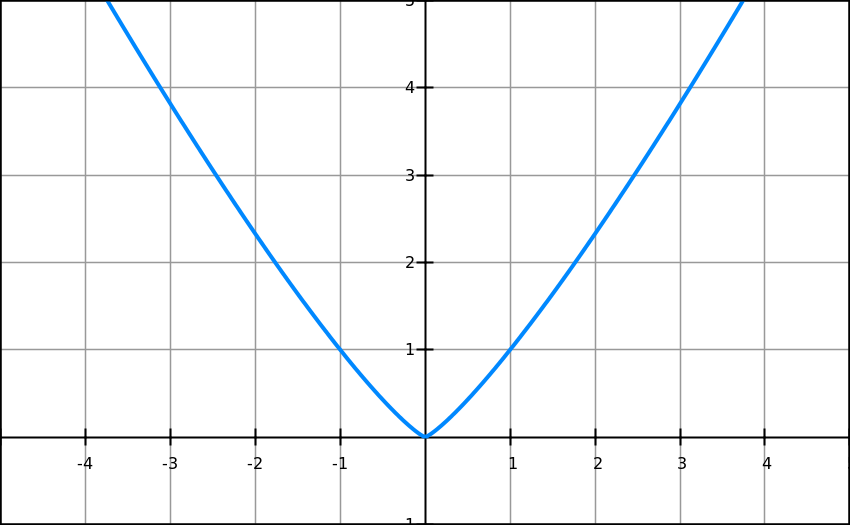
Figure 10
f(x)= Derivative
function will be: f ’(x)= When
f ’(x)=0 x=0 When
x=0 f(0)= Stationary
point for f(x)=
function is (0;0)
f(x)=
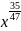
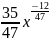
 f(0)=0
f(0)=0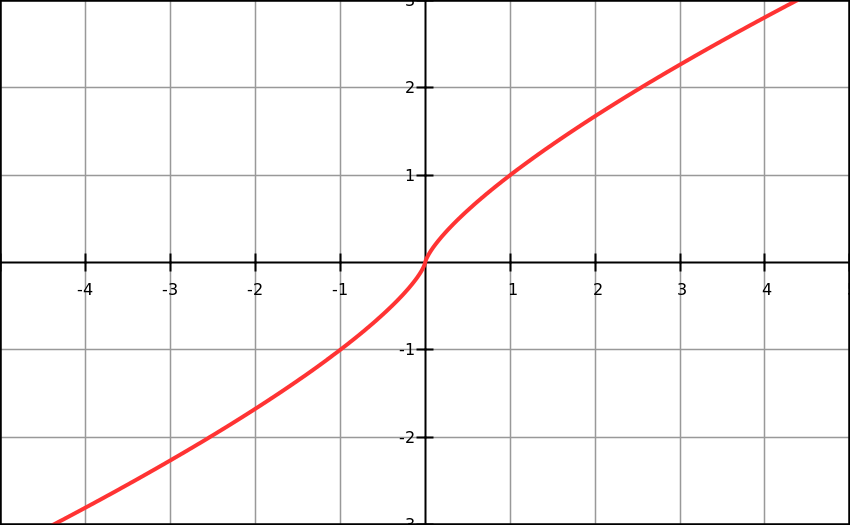
Conclusion:
Any Stationary points for function f(x)= are at (0;0) point or there is no Stationary Point at all.
To make a function with a fraction instead of a and with [∞;∞] domain – denominator should be odd number.
Fractions instead of a with numerator 1 have no minimum.
