75

САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ

ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ МЧС РОССИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

ПО ВЫСШЕЙ МАТЕМАТИКЕ

для слушателей заочного и дистанционного обучения

направление подготовки 280705.65 – Пожарная безопасность

квалификация (степень) – специалист

Санкт-Петербург

2013

Санкт-Петербургский университет

государственной противопожарной службы МЧС России

Калинина Е.С., Крюкова М.С., Медведева О.М.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

ПО ВЫСШЕЙ МАТЕМАТИКЕ

для слушателей 1 курса заочного и дистанционного обучения

направление подготовки 280705.65 – Пожарная безопасность

квалификация (степень) – специалист

Санкт-Петербург

2013

СОДЕРЖАНИЕ

Рекомендации по решению типовых задач по контрольной работе № 1 4

Рекомендации по решению типовых задач по контрольной работе № 2 20

Рекомендации по решению типовых задач по контрольной работе № 3 31

Рекомендации по решению типовых задач по контрольной работе № 4 40

Рекомендации по решению типовых задач по контрольной работе № 5 52

Рекомендации по решению типовых задач по контрольной работе № 6 61

Рекомендуемая литература 73

Рекомендации по решению типовых задач по контрольной работе № 1

1. Матрицы и операции над ними. Определители квадратных матриц.

Матрицей размера называется прямоугольная таблица чисел, содержащая строк и столбцов.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например , , , …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где – номер строки, – номер столбца. Матрица записывается в виде

.

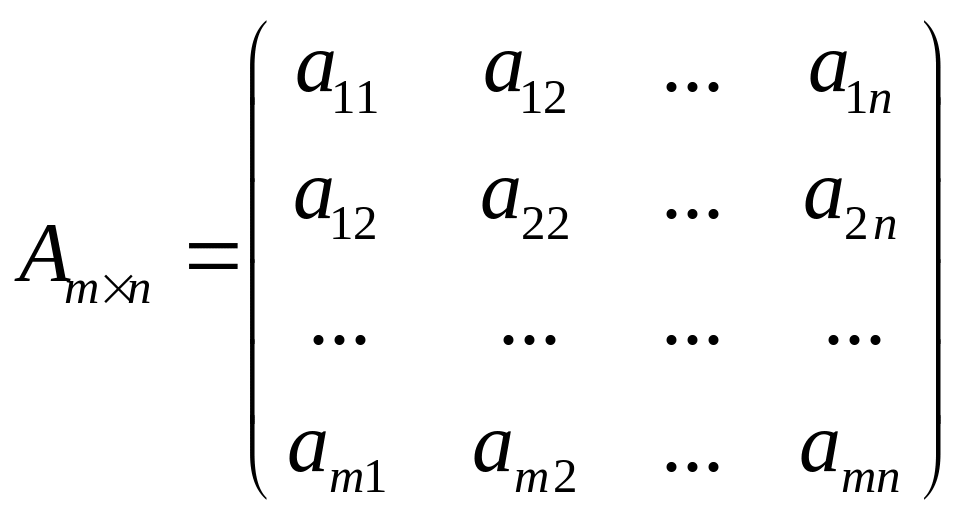Заметим, что матрицы и есть матрицы разного порядка.

Две матрицы и одного размера называются равными, если равны все соответствующие элементы этих матриц, т.е. , если , где , .

Виды матриц.

1. Матрица-строка – матрица, состоящая из одной строки. Например, – матрица-строка.

2. Матрица-столбец – матрица, состоящая из одного столбца. Например, 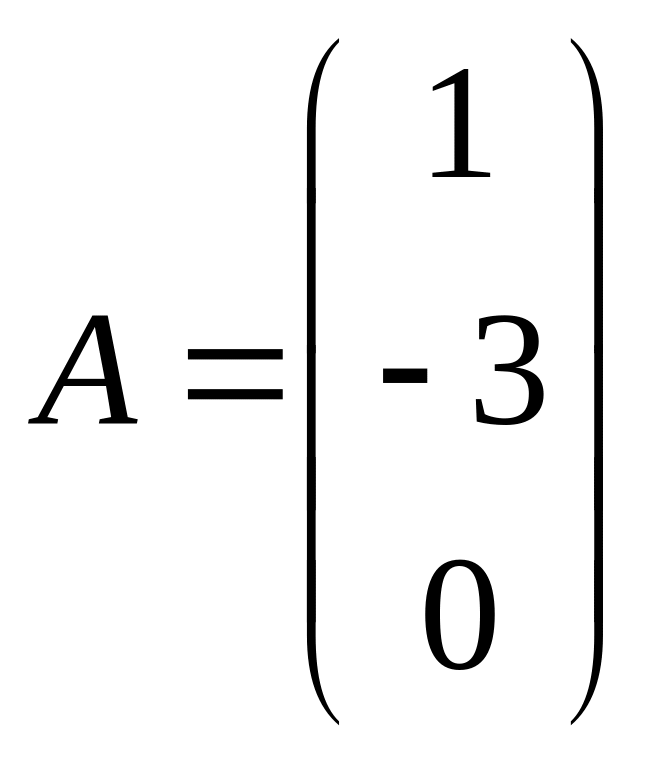– матрица-столбец.

3. Квадратная матрица – матрица, у которой число строк равно числу столбцов. Например, 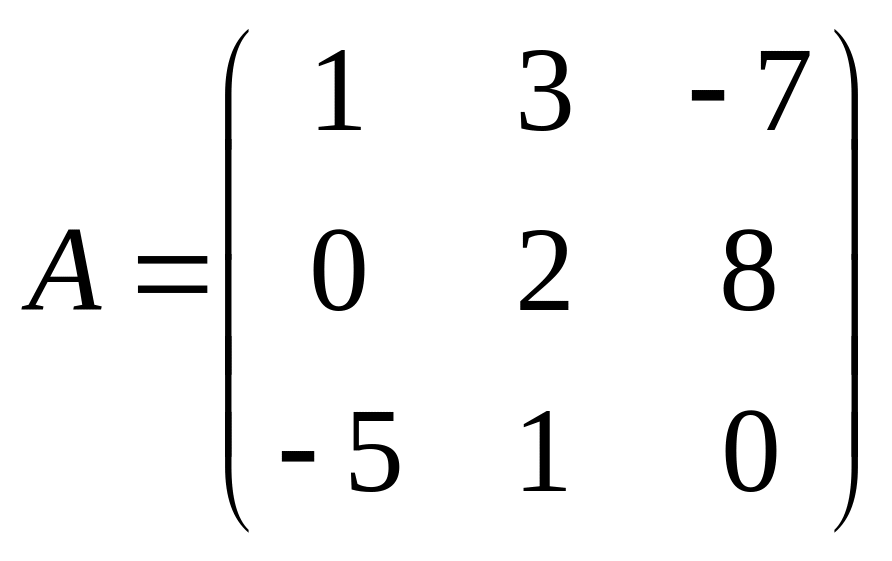– квадратная матрица третьего порядка.

4. Диагональная матрица – квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю. Например, 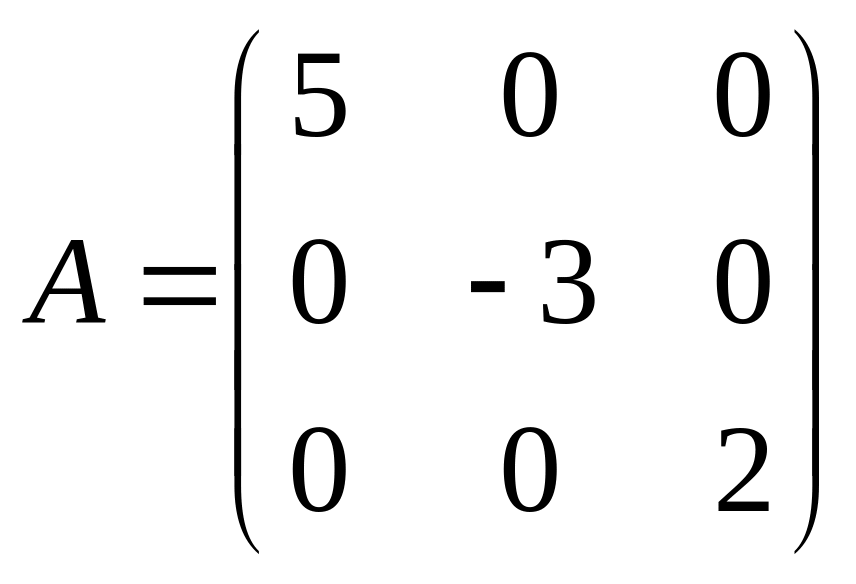– диагональная матрица третьего порядка.

5. Единичная матрица – диагональная матрица, у которой каждый элемент главной диагонали равен единице. Например, 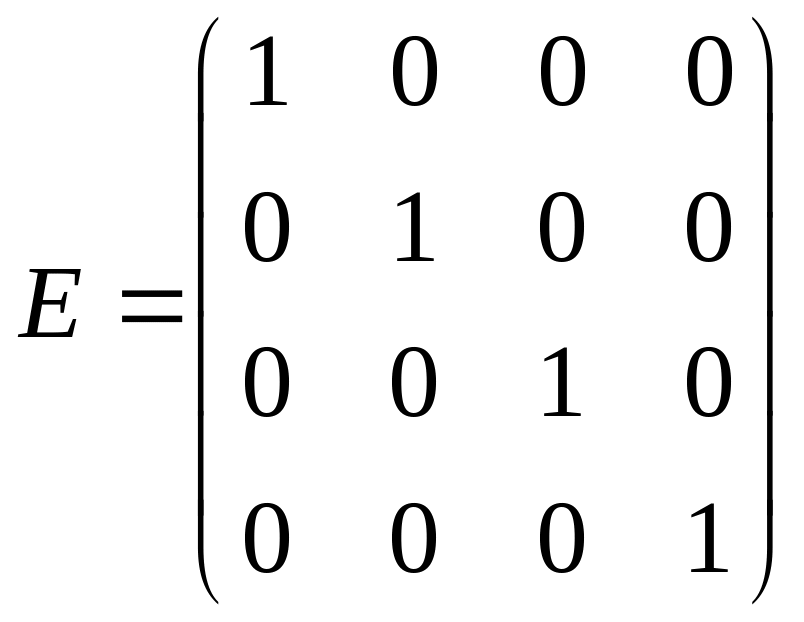– единичная матрица четвертого порядка.

6. Нулевая матрица – матрица, все элементы которой равны нулю. Например, 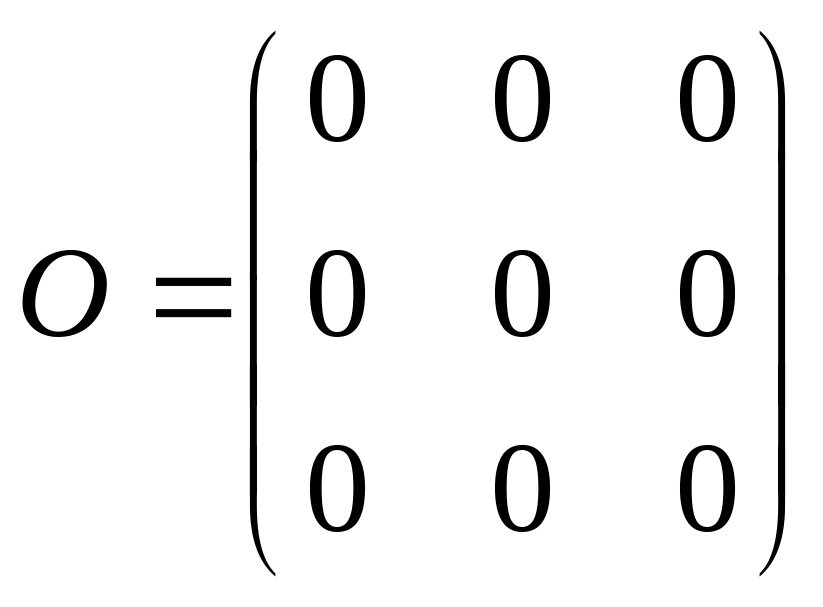– нулевая матрица третьего порядка.

7. Транспонированная матрица – матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером. Например, для матрицы , транспонированная матрица имеет вид .

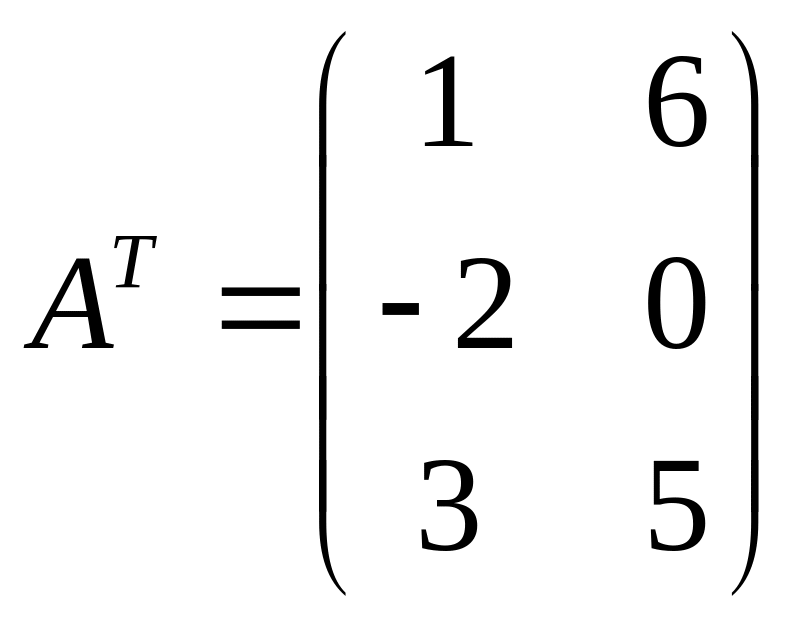Над матрицами, как и над числами можно производить ряд операций, причем.

Умножение матрицы на число. Произведением матрицы на число (или числа на матрицу А) называется матрица , элементы которой , ( , ).

Пример 1.1. Умножить матрицу на число 4.

Решение. .

Сложение матриц. Суммой двух матриц и одинакового размера называется матрица , элементы которой , ( , ).

Пример 1.2. Пусть 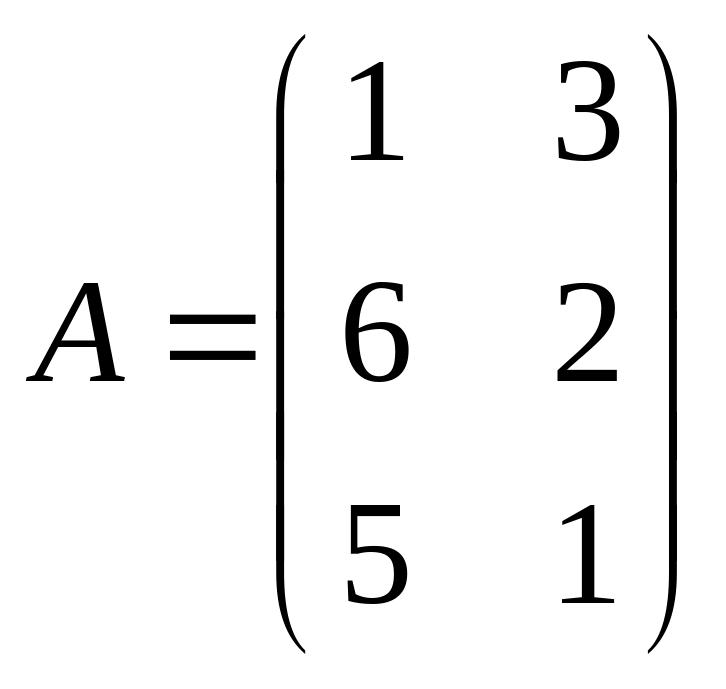, 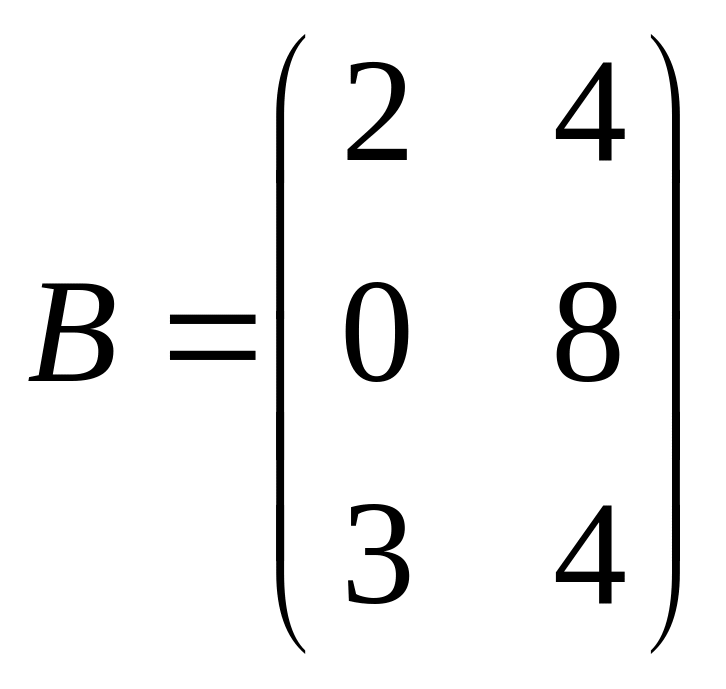. Найти .

Решение. .

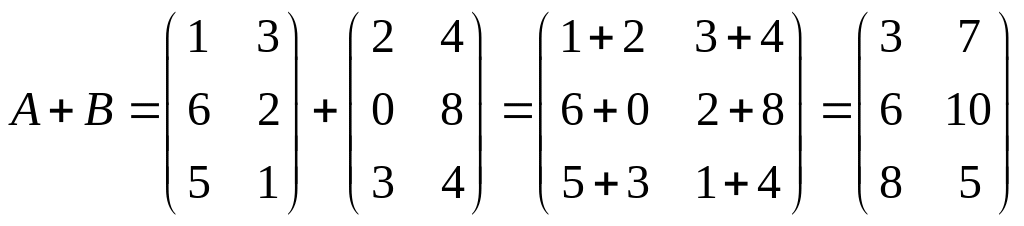Вычитание матриц. Разность двух матриц одинакового размера определяется через операции сложения матриц и умножения матрицы на число: .

Пример 1.3. Пусть , . Найти .

Решение. .

Произведение матриц. Произведение матриц имеет место только для матриц определенных размерностей. Матрицу можно умножить на матрицу , если число столбцов матрицы равно числу строк матрицы , т.е. если имеет размерность , то матрица должна иметь размерность . Произведением будет матрица размерности .

Произведением матриц называется матрица , каждый элемент которой равен сумме произведений элементов строки матрицы на соответствующие элементы столбца матрицы .

Получение элемента схематично изображается так:

Пример 1.4. Вычислить произведение матриц , где , .

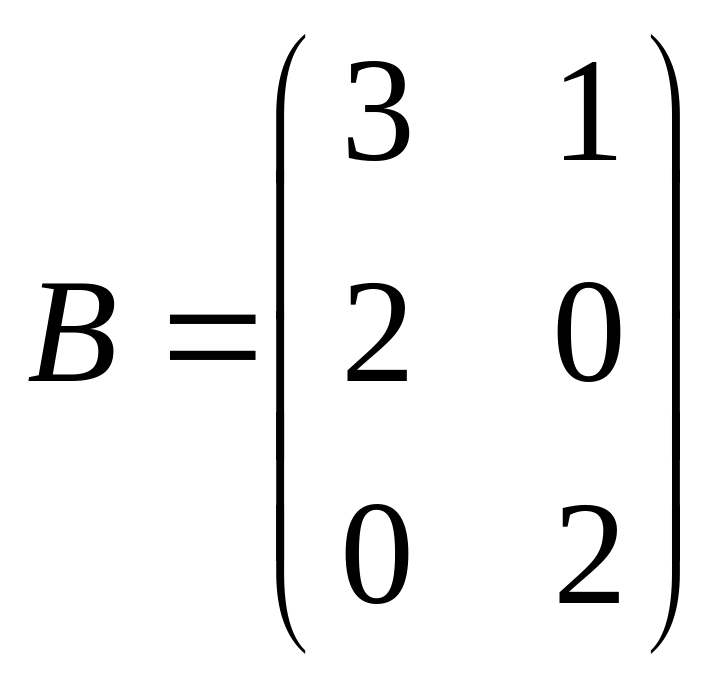Решение. Найдем размер матрицы-произведения: . Вычислим элементы матрицы-произведения , умножая элементы строки матрицы на соответствующие элементы столбцов матрицы : .

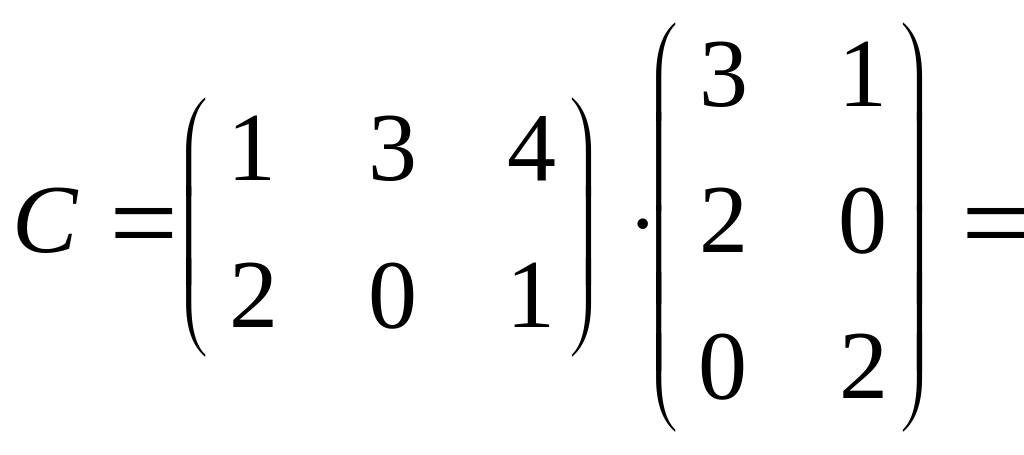
Пример 1.5. Найти матрицу , если , , .

Решение. Произведение матриц и возможно. Умножая элементы строки матрицы на соответствующие элементы столбцов матрицы , получим .

Умножим матрицу на число 2, получим

. Найдем сумму матриц и :

.

Определитель (детерминант) – это число, соответствующее данной квадратной матрице и вычисленное по определенному правилу.

Для обозначения определителей используются следующие символы: , , . Символ обозначает таблицу (матрицу), для которой вычисляется определитель.

Определитель матрицы первого порядка или просто определитель первого порядка равен самому числу : .

Например, пусть , тогда .

Определителем матрицы второго порядка 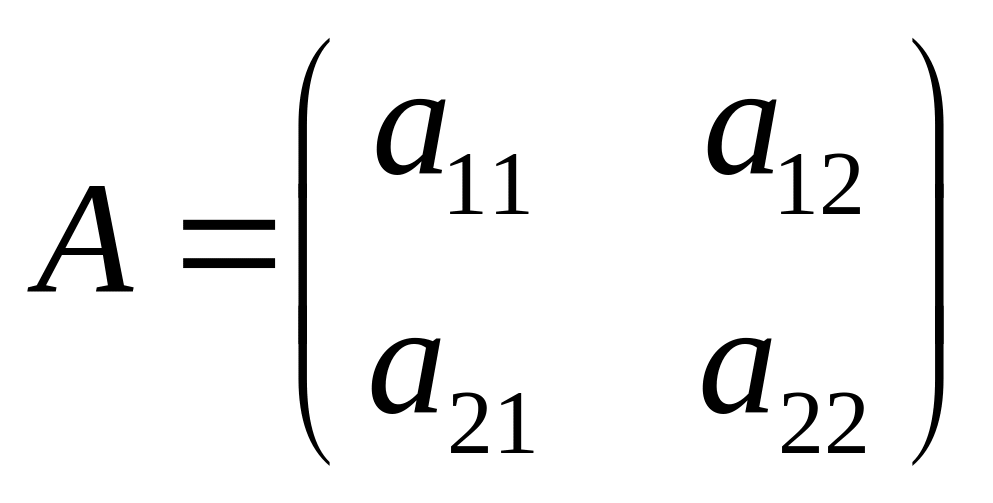, или определителем второго порядка называется число, которое вычисляется по формуле: .

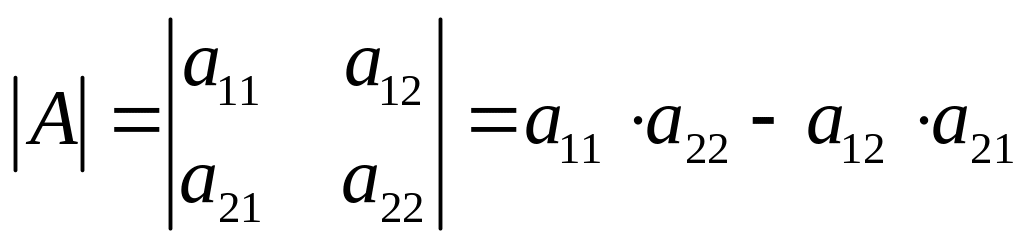Например, пусть , тогда .

Определителем матрицы третьего порядка 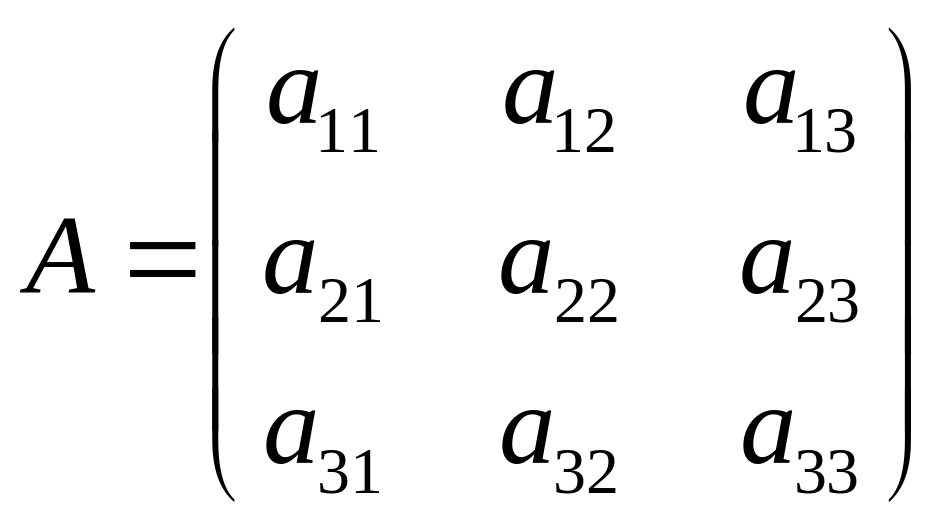или определителем третьего порядка называется число, которое вычисляется по формуле: .

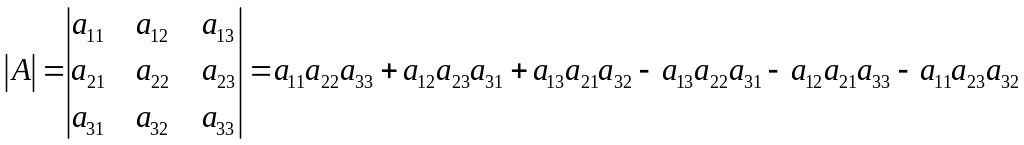Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы.

Вычисление определителя третьего порядка иллюстрируется схемой:

.

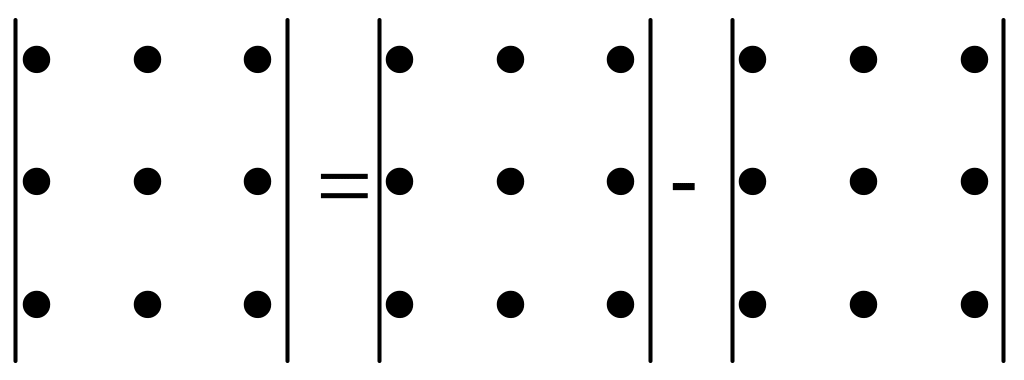
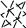
Пример 1.6. Вычислить определители третьего порядка .

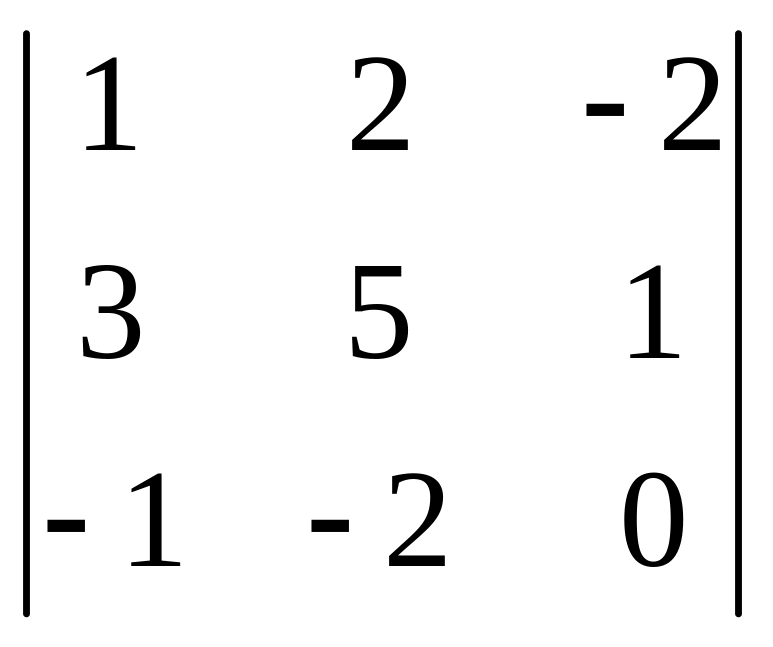Решение.

.

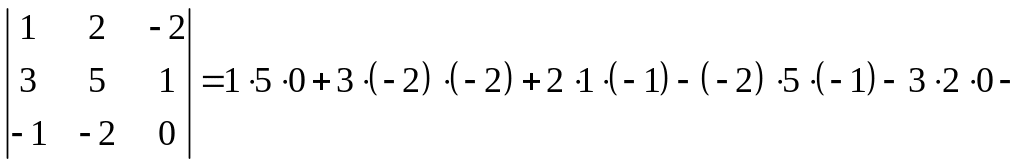
Минором элемента матрицы порядка называется определитель матрицы порядка, полученной из матрицы вычеркиванием строки и столбца.

Пример 1.7. Найти минор элемента матрицы третьего порядка .

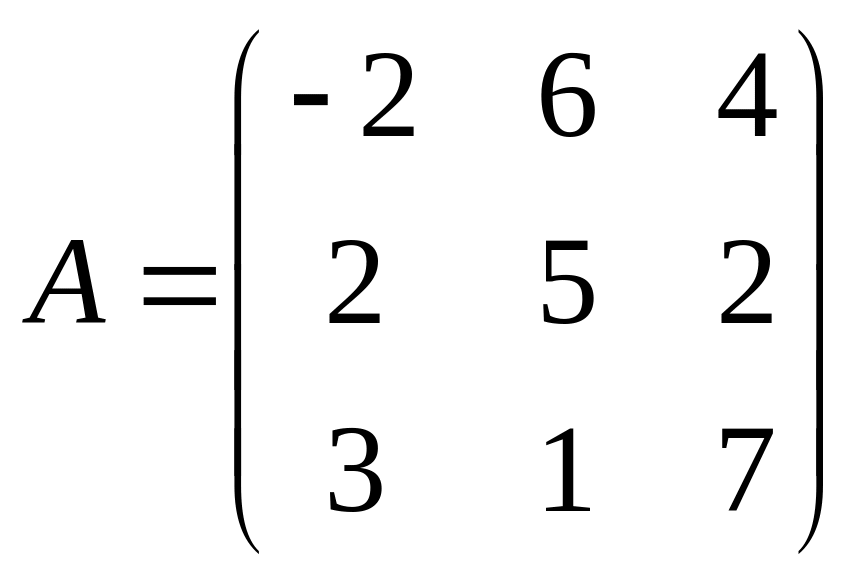Решение. Из полученной матрицы вычеркнем первую строку, и третий столбец, получим .

Алгебраическим дополнением элемента матрицы порядка называется его минор, взятый со знаком : .

Пример 1.8. Найти алгебраическое дополнение элемента матрицы третьего порядка .

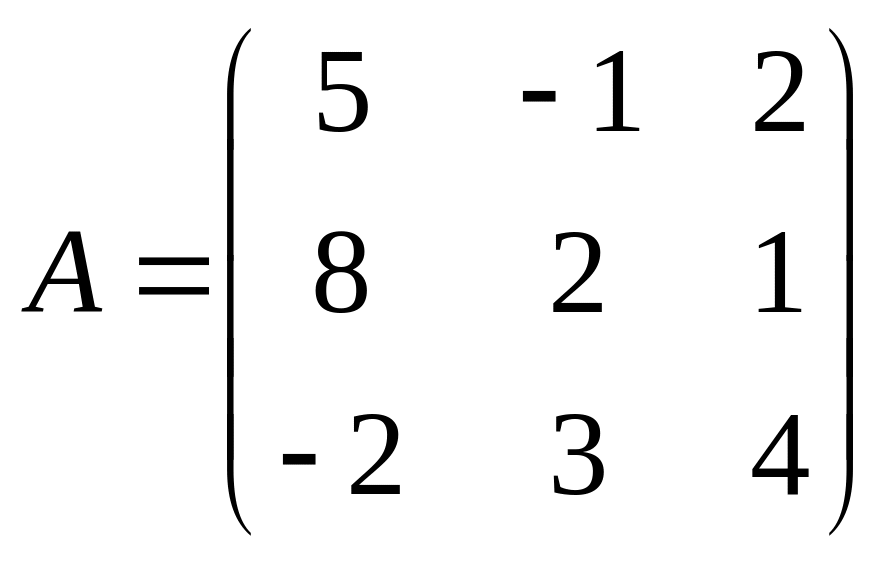Решение. Из полученной матрицы вычеркнем первую строку, и второй столбец, полученный минор возьмем со знаком , т.е. .