ГОУ ВПО

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ И ПРЕДПРИНИМАТЕЛСТВА

ПЕНЗЕНСКИЙ ФИЛИАЛ

Ю.Ю. ГОРЮНОВ, Т.Ю. ГОРЮНОВА, Д.В. Дружинин

Теория и методы принятия решений

Учебное пособие

ПЕНЗА 2010

Теория и методы принятия решений (ТиМПР) – это наука, которая математическими методами обосновывает выбор одного из нескольких решений задачи (проблемы). Следует подчеркнуть, что окончательное решение принимает лицо ответственное за принятие решений, причём его выбор не всегда совпадает с рекомендуемым.

Некоторые разделы ТиМПР:

• математическое программирование (линейное программирование, нелинейное программирование, …);

• динамическое программирование;

• сетевое планирование;

• потоки в сетях;

• принятие решений в условиях неопределённости (теория игр).

Для применения ТиМПР необходимо:

1. сформулировать задачу (проблему);

2. создать математическую модель (формализовать задачу в математической форме);

3. решить математическую модель, используя соответствующий раздел ТиМПР;

4. сформулировать предложения для принятия решения.

1. Математическое программирование

1.1. Линейное программирование

Задача. Предприятие располагает тремя видами сырья, из которого изготавливает два вида продукции. Количество сырья, необходимого для производства каждого вида продукции, и доход от продажи единицы каждого вида приведены в следующей таблице:

Сырьё	Запасы	Расход сырья на изделие
		I	II
I	21	3	4
II	30	2	3
III	16	1	2
Доход от продажи		3	2

Требуется составить план выпуска продукции, при котором доход от продажи был бы максимальным.

Формализация (создание математической модели). Обозначим через x₁ количество изготовленных изделий вида I, а через x₂ – вида II. Тогда, учитывая имеющиеся запасы сырья, получим систему неравенств:

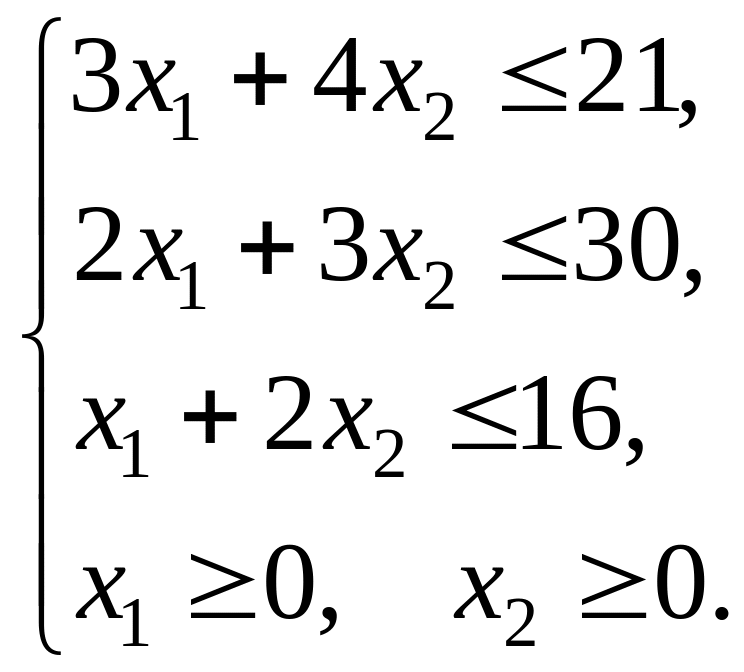(1)

а доход от продажи составит

Таким образом, для определения максимального дохода от продажи изделий необходимо найти максимальное значение функции при условии выполнения системы неравенств (1) – это и есть математическая модель поставленной задачи.

Полученная математическая модель состоит из системы ограничений в виде системы линейных неравенств (1) и линейной целевой функции , для которой требуется найти максимальное значение.

Задачи, в которых требуется найти максимальное (или минимальное) значение линейной целевой функции, при условии выполнения системы ограничений в виде системы линейных уравнений и/или неравенств, относятся к задачам линейного программирования.

Упражнения

Составьте математическую модель задачи и обоснованно ответьте на вопрос: относится ли она к задачам линейного программирования?

1. Для изготовления трёх видов изделий используется четыре вида оборудования. Затраты времени на обработку одного изделия на каждом виде оборудования, общий фонд рабочего времени оборудования¹ и прибыль от продажи единицы изделия приведены в таблице:

Тип оборудования	Затраты времени на обработку одного изделия			Общий фонд рабочего времени оборудования
	I	II	III
I	2	4	5	120
II	1	8	6	280
III	7	4	5	240
IV	4	6	7	360
Прибыль:	10	14	12

Требуется определить, сколько изделий и какого вида следует изготовить, чтобы получить максимальную прибыль от их продажи.

2. Молочный завод производит молоко, кефир и сметану. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. Затраты рабочего времени на разлив 1 т молока, сметаны и кефира составляют соответственно 0,18, 0,19 и 3,25 часов. Общий объём используемого молока заводом в сутки не превышает 136000 кг. Оборудование, используемое для разлива молока и кефира, может работать в сутки не более 21,4 часа, а сметаны – не более 16,25 часа. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 3000, 2200 и 1360 рублей. Завод должен производить не менее 100 т молока.

Определить план выпуска заводом молочной продукции, который обеспечивает заводу максимальную ежедневную прибыль.