Моп_Л2_2сИНФ,ПМ.doc во многом – воспоминание о 1-м семестре

Лекция 2. Сходимость и обзор непрямых методов.

1. Метод модифицированных функций Лагранжа (метод множителей), метод штрафных функций

Вспомним рассмотренную в 1-м семестре модифицированную функцию Лагранжа: , зависящую от параметра c. Далее под x* будем понимать точку локального минимума задачи с ограничениями-равенствами h(x)=0, удовлетворяющую достаточным условиям оптимальности второго порядка.

Итерация метода множителей состоит в следующем.

При заданных векторе и значении штрафного параметра вектор определяется как точка минимума на . Затем вычисляется вектор

, (1)

выбирается новое значение параметра штрафа и осуществляется переход к следующей итерации. Начальный вектор выбирается произвольно, а последовательность либо задается заранее, либо строится по ходу итеративного процесса с учетом получаемых результатов.

Теоретически доказано, что метод множителей сходится линейно, если последовательность ограничена, и сверхлинейно, если - неограниченно возрастающая последовательность.

Вспомним теперь задачу нелинейного программирования, ограничения которой наряду с равенствами содержат и неравенства.

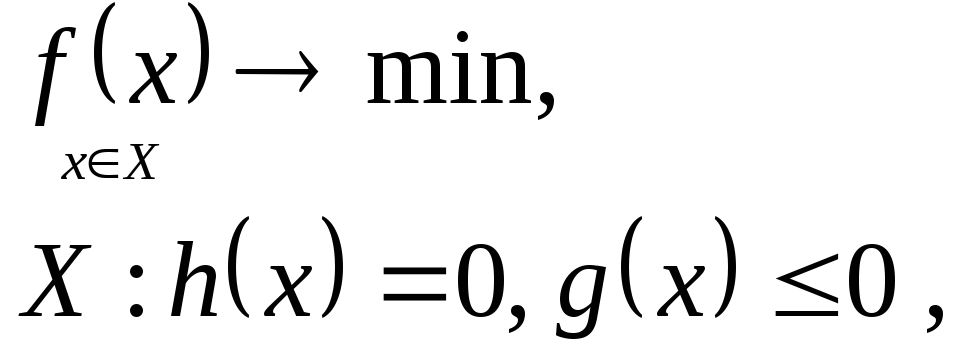(2)

где заданные функции, причем, .

Было получено следующее выражение для модифицированной функции Лагранжа задачи :

Пусть точка минимума . Метод множителей первого порядка для задачи (2) определяется соотношениями:

, ,

где , вектор .

Можно записать: ,

или окончательно

, (3)

где через обозначается j-ая координата вектора .

Соотношение (3)3) является для метода множителей первого порядка формулой пересчета вектора множителей, соответствующего ограничениям в форме равенств. Из этого соотношения видно, что если , то через конечное число итераций те множители , которые соответствуют ограничениям, не активным в точке , обратятся в нуль.

Напомним, что Методы штрафных функций относятся к группе непрямых методов решения задач нелинейного программирования. В общем случае вспомогательная функция имеет вид F(x,a) f(x) +Ф(х, а).

Здесь f(x) - целевая функция задачи оптимизации; Ф(х, а) - “штрафная” функция; параметр а >0. Точку безусловного минимума функции F(x, a) будем обозначать через х(а). В зависимости от вида Ф(х, а) различают методы внутренних штрафных, или барьерных, функций и методы внешних штрафных функций.

2. Сравнение метода множителей с методом штрафа (последовательной безусловной оптимизации)

В отличие от метода множителей, где вектор множителей пересчитывается по формуле

, (4)

в методе штрафа подобный пересчет не используется. Теорема о сходимости, относящаяся к обоим этим методам, дает естественный способ их сравнения.

Можно показать, что в методе множителей для достижения сходимости не требуется устремлять к бесконечности. Напротив, в методе штрафа, где , неограниченное увеличение , как правило, необходимо. Указанное обстоятельство является важным преимуществом метода множителей. Оно означает, что в методе множителей нет проблемы плохой обусловленности, или, во всяком случае, эта проблема не является столь острой, как в методе штрафа. Кроме того, метод множителей сходится значительно быстрее метода штрафа, и это является его вторым преимуществом. Если метод множителей обычно сходится линейно или даже сверхлинейно, то скорость сходимости метода штрафа зависит от скорости увеличения параметра штрафа, и, как правило, оказывается гораздо более низкой. Согласно экспериментальным данным, метод множителей с пересчетом по формуле (4) обеспечивает экономию машинного времени по сравнению с методом штрафа на 30-80 %. Однако, на практике большое значение имеет выбор начального приближения для вектора множителей Лагранжа и последовательности значений параметра штрафа. Целесообразно попытаться выбрать по возможности более близким к , используя для этого имеющуюся априорную информацию о решении. Параметр штрафа на практике рекомендуют выбирать следующим образом. Начальное значение выбирают относительно небольшим. В ходе итеративного процесса монотонно увеличивают, используя соотношение с числовым множителем . При этом, начиная с некоторой итерации, заведомо окажется большим порогового значения.

Естественная схема пересчета параметра штрафа, отличная от приведенной выше, состоит в том, чтобы умножать на лишь в тех случаях, когда не обеспечивается линейная (с фиксированным знаменателем ) скорость убывания модуля невязки ограничений . Соответствующая формула пересчета имеет вид:

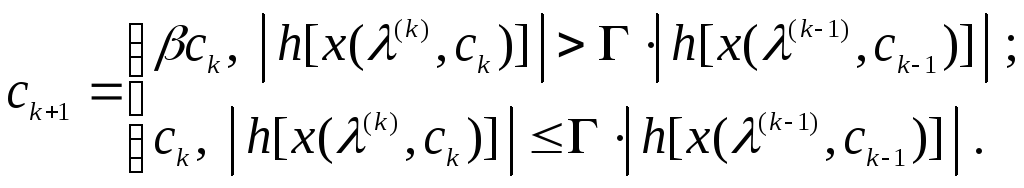
Стандартный выбор параметров в этой схеме: .