
Лекция 6
.docЛекция 6
Нелинейное программирование (НП)
Как известно, задачи НП можно представить в следующем обобщенном виде:
![]() (1)
(1)
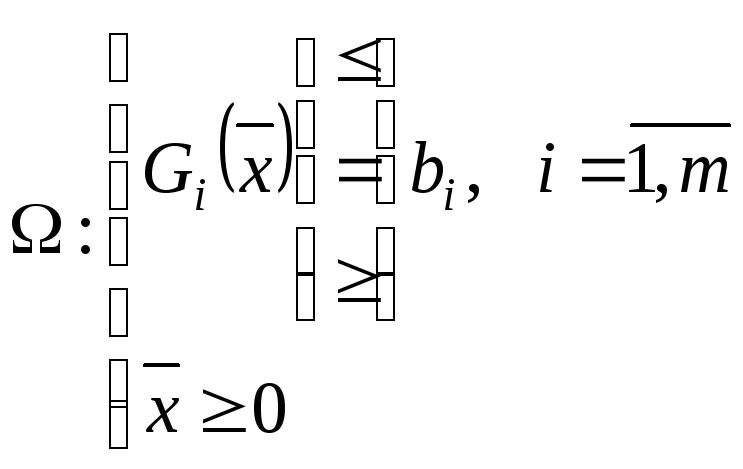
![]()
Целевая функция
![]() и функции
и функции
![]() ,
определяющие ОДР
,
определяющие ОДР
![]() ,
в общем случае нелинейные функции
переменных
,
в общем случае нелинейные функции
переменных
![]() .
.
Если
![]() - нелинейная функция, а
- нелинейная функция, а
![]() - линейные функции, то говорят о задаче
НП с линейными ограничениями.
- линейные функции, то говорят о задаче
НП с линейными ограничениями.
К числу задач НП
с линейными ограничениями относится
задача квадратичного программирования
(КП). В этой задаче
![]() - квадратичная форма, а
- квадратичная форма, а
![]() - линейные функции. Иными словами, задача
КП – задача минимизации квадратичной
формы при линейных ограничениях.
- линейные функции. Иными словами, задача
КП – задача минимизации квадратичной
формы при линейных ограничениях.
Заметим, что к числу задач (1), (2), (3) относится ранее изученная задача условной оптимизации:
![]() (4)
(4)
![]() (5)
(5)
Универсального
метода решения задач НП (подобного СМ
решения задач ЛП) не существует, однако,
для задач нелинейного выпуклого
программирования (НВП), т.е. в случае,
когда целевая функция
![]() - выпуклая функция и функции
- выпуклая функция и функции
![]() - выпуклые функции, существует ряд
эффективных методов решения.
- выпуклые функции, существует ряд
эффективных методов решения.
1. Обобщение ММЛ. Теорема Куна-Таккера. Локальные условия Куна-Таккера
Ранее был изучен ММЛ для решения классической задачи условной оптимизации. Этот метод позволяет исходную задачу классической условной оптимизации преобразовать в задачу безусловной оптимизации путем введения функции Лагранжа вида:
![]() , (6)
, (6)
что позволяют
решать задачу безусловной оптимизации
(БО)
![]() ;
необходимые условия имеют вид:
;
необходимые условия имеют вид:
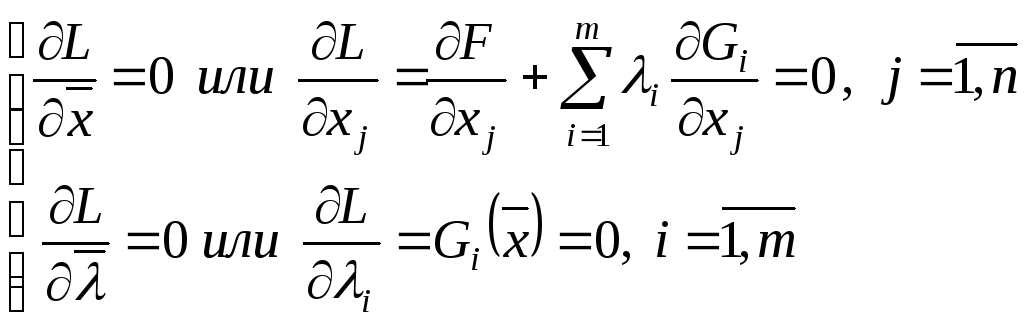
![]()
Классическую задачу условной оптимизации (КЗУО) можно рассматривать как задачу о нахождении седловой точки функции Лагранжа, т.е. имеет место неравенство:
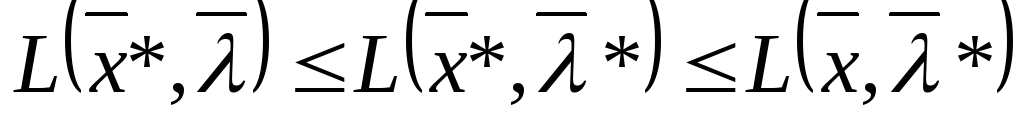 ,
(9)
,
(9)
где
![]() -
-
![]() -мерная
точка минимума, а
-мерная
точка минимума, а
![]() -
-
![]() -мерная
точка максимума.
-мерная
точка максимума.
Применим ММЛ к решению задачи НП общего (симметрического) вида:
![]() (10)
(10)
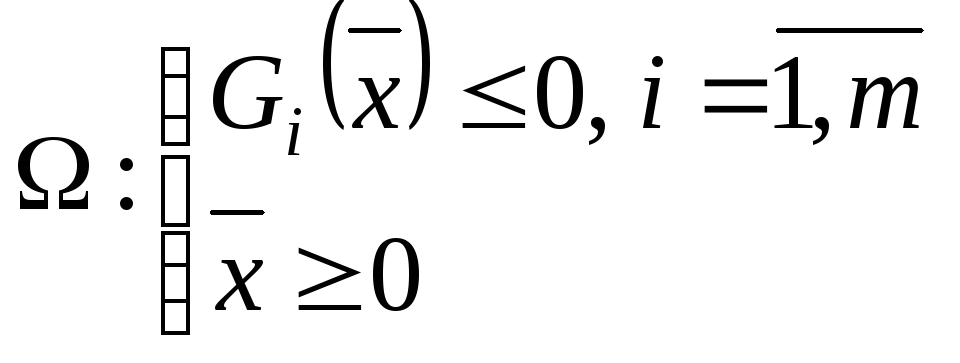
![]()
Обоснованием применимости является теорема Куна-Таккера.
Теорема 1
Предположим, что
существует вектор
![]() ,
такой, что
,
такой, что
![]() ,
,
![]() ,
тогда необходимым и достаточным условием
минимальности вектора
,
тогда необходимым и достаточным условием
минимальности вектора
![]() ,
принадлежащего допустимой области
,
принадлежащего допустимой области
![]() является существование такого вектора
является существование такого вектора
![]() ,
что для всех
,
что для всех
![]() ,
,
![]() ,
выполняются неравенства (9), то есть:
,
выполняются неравенства (9), то есть:
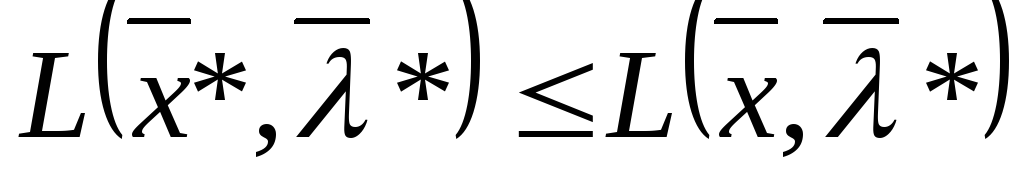 (9')
(9')
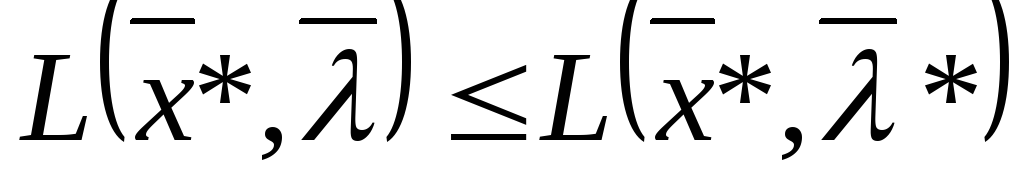 (9'')
(9'')
Тогда выполняются локальные условия Куна-Таккера:
Из (9')![]()
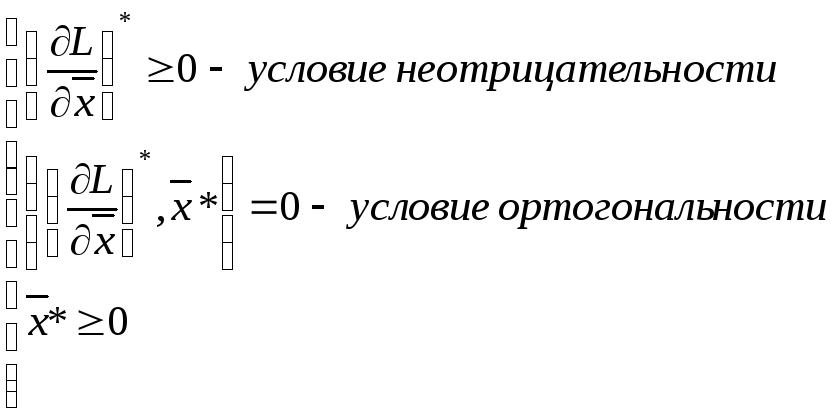
![]()
Из (9")![]()
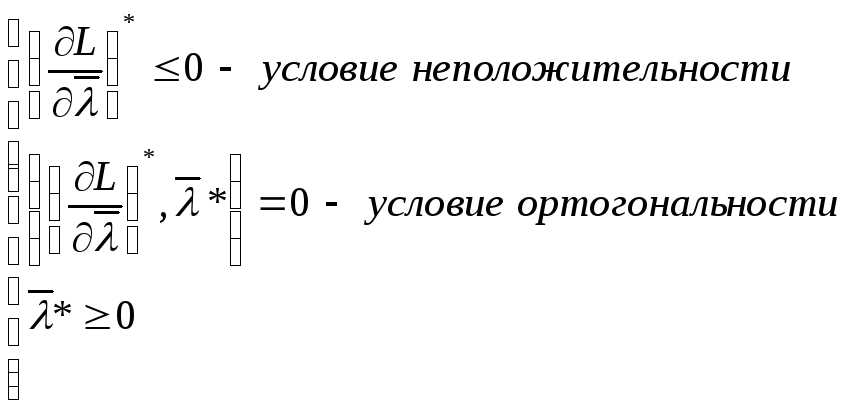
![]()
И наоборот, например, из неравенств (13), (14), (15), следует (9').
Доказательство.
Разложим в
окрестности точки
![]() функцию
функцию
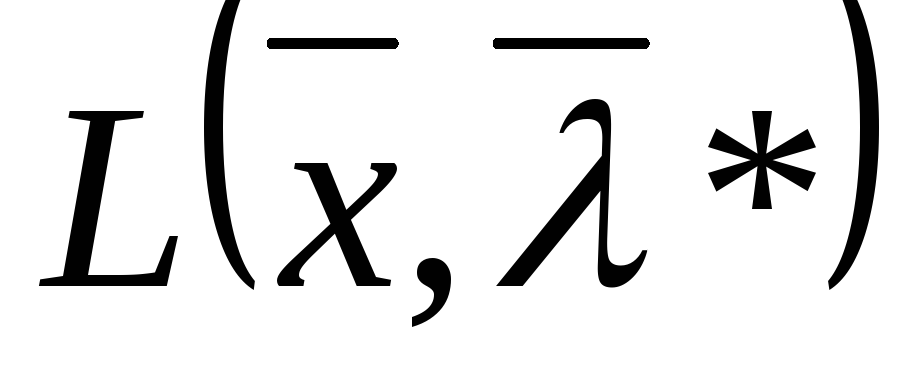 в ряд Тейлора:
в ряд Тейлора:
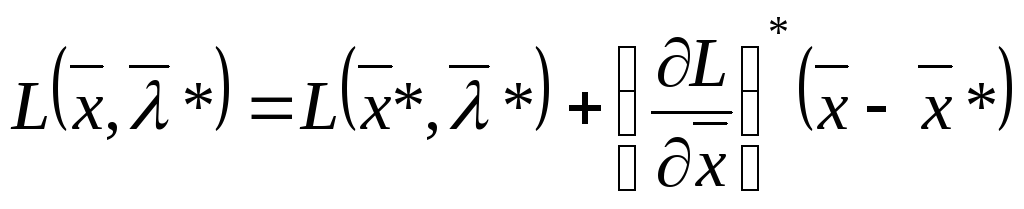 (19)
(19)
В разложении учтены только линейные по приращению аргументов слагаемые. Тогда, из (14), или (17) следует:
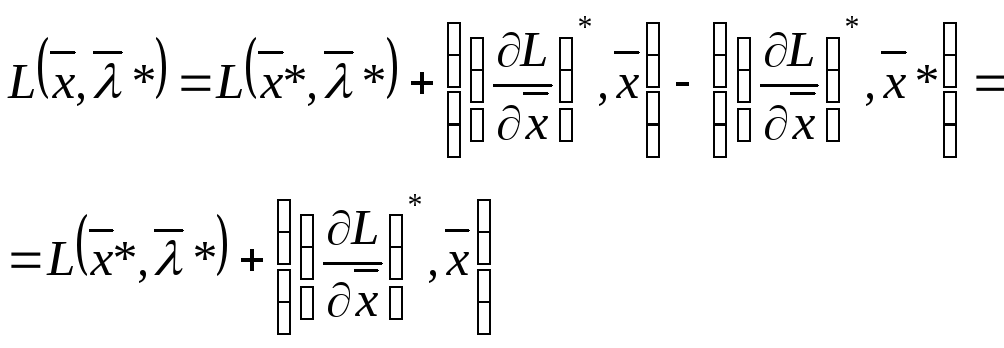
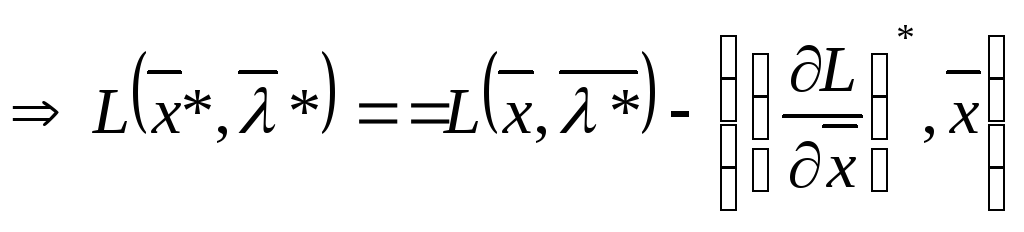 (20)
(20)
Из (13) и (20) с очевидностью следует неравенство (9').
Аналогично можно доказать, что если в качестве исходного взять (9') и (9") – условия седловой точки, то справедливы условия Куна-Таккера, соответственно (13)-(18).
Локальные условия Куна-Таккера – необходимые условия решения задачи НП вида (10), (11), (12) – это аналог необходимых условий (7)-(8) в задаче классической условной оптимизации.
2. Обзор методов решения задач нелинейного программирования
2.1. Градиентные методы
В задачах НВП
целевая функция
![]() и функции, представляющие неравенства
ограничений (функции, определяющие ОДР
и функции, представляющие неравенства
ограничений (функции, определяющие ОДР
![]() )
-
)
-
![]() ),
есть нелинейные выпуклые функции.
),
есть нелинейные выпуклые функции.
Отметим, что если
целевая функция
![]() содержит единственную экстремальную
точку
содержит единственную экстремальную
точку
![]() внутри области
внутри области
![]() ,
то для решения такой задачи НВП можно
воспользоваться методами решения задач
безусловной оптимизации, например,
градиентным.
,
то для решения такой задачи НВП можно
воспользоваться методами решения задач
безусловной оптимизации, например,
градиентным.
Если же
![]() достигает экстремального значения в
точке, находящейся на границе
достигает экстремального значения в
точке, находящейся на границе
![]() ,
то градиентные методы применимы также,
однако, имеются сложности при применении.
,
то градиентные методы применимы также,
однако, имеются сложности при применении.
Среди задач НВП различают:
-
задачи с линейными ограничениями;
-
задачи с нелинейными ограничениями.
В задачах с линейными
ограничениями
![]() - нелинейная выпуклая функция, а
- нелинейная выпуклая функция, а
![]() - линейные функции.
- линейные функции.
Задачи НВП с
нелинейными ограничениями содержат
![]() и
и
![]() ,
,
![]() - нелинейные выпуклые функции.
- нелинейные выпуклые функции.
2.2. Задачи НВП с линейными ограничениями
![]() (21)
(21)
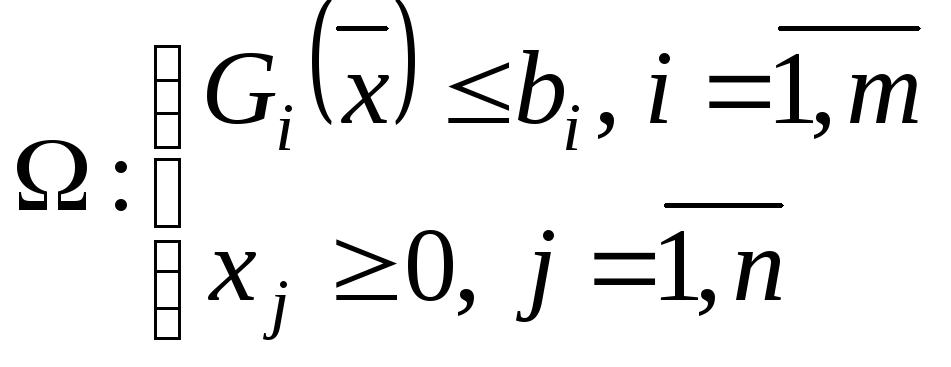
![]() - нелинейная
выпуклая функция.
- нелинейная
выпуклая функция.
![]() ,
,
![]() (22)
(22)
Геометрическая
интерпретация решения этой задачи в
![]() имеет
вид:
имеет
вид:

![]() ,
т.к.
,
т.к.
![]() - острый угол. (23)
- острый угол. (23)
Направление
![]() находится из условия максимизации
скалярного произведения (23).
находится из условия максимизации
скалярного произведения (23).
![]() - условие
экстремальности.
- условие
экстремальности.
![]() ;
;
![]() .
.
Траектория точки
![]() при поиске максимума
при поиске максимума
![]() .
.
2.3. Метод Франка-Вульфа
Метод позволяет исходную задачу НВП с линейными ограничениями (21-22) преобразовать в задачу ЛП.
Нелинейную выпуклую
целевую функцию
![]() аппроксимируем линейной функцией
переменных
аппроксимируем линейной функцией
переменных
![]() ,
причем, коэффициентами этой аппроксимации
являются проекции
,
причем, коэффициентами этой аппроксимации
являются проекции
![]() ;
аппроксимация осуществляется на каждой
итерации.
;
аппроксимация осуществляется на каждой
итерации.
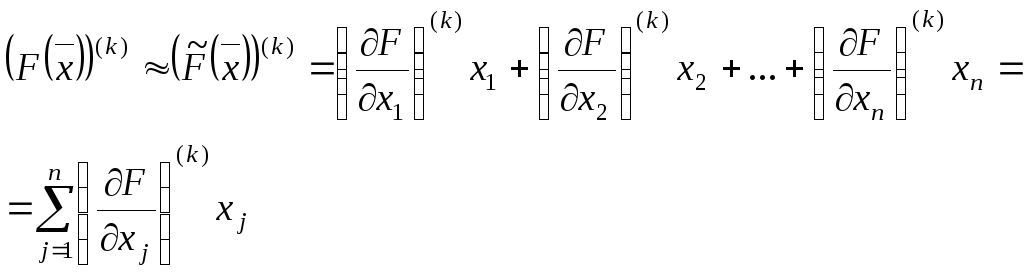 (24)
(24)
Теперь очевидно, что (24), (21), (22) представляют задачу ЛП, которая решается универсальным эффективным СМ.
Итак, на каждой
итерации в результате решения задачи
ЛП находим оптимальное решение
![]() .
.
Итерационная формула, позволяющая найти решение исходной задачи, имеет вид:
![]()
![]() находится в
результате решения уравнения:
находится в
результате решения уравнения:
![]() .
.
Итерационный поиск
точки экстремума
![]() исходной целевой функции
исходной целевой функции
![]() продолжаются до выполнения условий:
продолжаются до выполнения условий:
![]() .
.
2.4. Задачи (21) – НВП с нелинейными ограничениями
Пусть в (21)
![]() ,
,
![]() - нелинейные выпуклые функции
- нелинейные выпуклые функции
![]() .
.
Геометрическая интерпретация в R2:
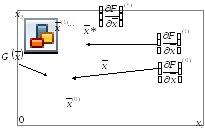
![]() - условие
коллинеарности векторов в точке
максимума.
- условие
коллинеарности векторов в точке
максимума.
Условие коллинеарности является условием окончания вычисления.
Итак, применение
градиентных методов к решению задач
НВП с линейными и нелинейными ограничениями
имеет ряд особенностей по сравнению с
применением градиентных методов к
решению задач безусловной оптимизации.
Эти особенности связаны с наличием
границы ОДР
![]() и хорошо проиллюстрированы на
соответствующих рисунках.
и хорошо проиллюстрированы на
соответствующих рисунках.
2.5. О задаче квадратичного программирования (КП) и методе ее решения
Рассмотрим ЗНП,
где целевая функция
![]() – квадратичная форма (квадратичная
функция переменных
– квадратичная форма (квадратичная
функция переменных
![]() ),
а функции
),
а функции
![]() ,
представляющие ОДР
,
представляющие ОДР
![]() - линейные формы (линейные функции
переменных
- линейные формы (линейные функции
переменных
![]() ).
).
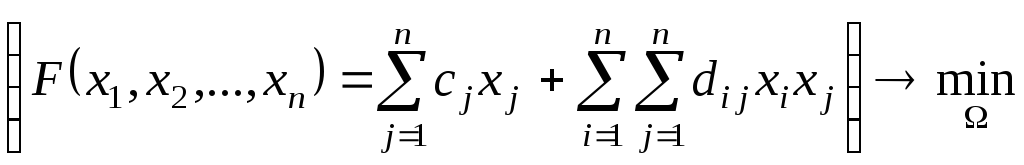 (25)
(25)
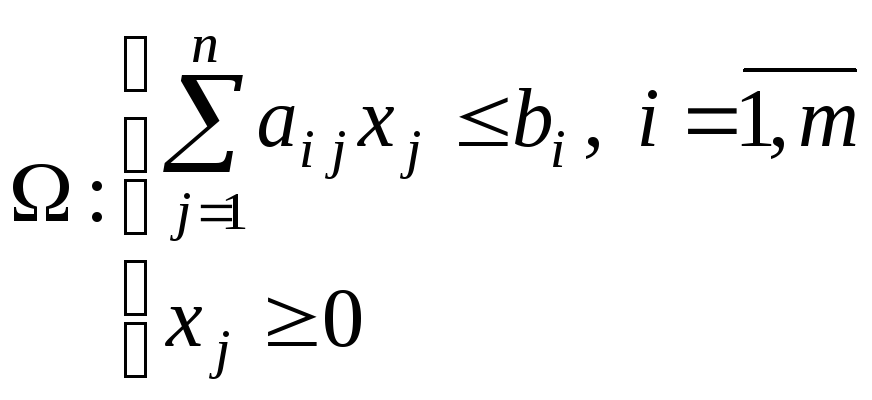 (26)
(26)
![]() - элементы
симметричной, положительно определенной
матрицы
- элементы
симметричной, положительно определенной
матрицы
![]() квадратичной формы.
квадратичной формы.
Точка минимума
![]() в задаче КП, в отличие от задачи ЛП, может
находиться как на границе области
в задаче КП, в отличие от задачи ЛП, может
находиться как на границе области
![]() ,
так и внутри этой области.
,
так и внутри этой области.
Задача КП достаточно эффективно решается ММЛ (обобщенным ММЛ).
Функция Лагранжа
![]() для задачи КП имеет вид.
для задачи КП имеет вид.
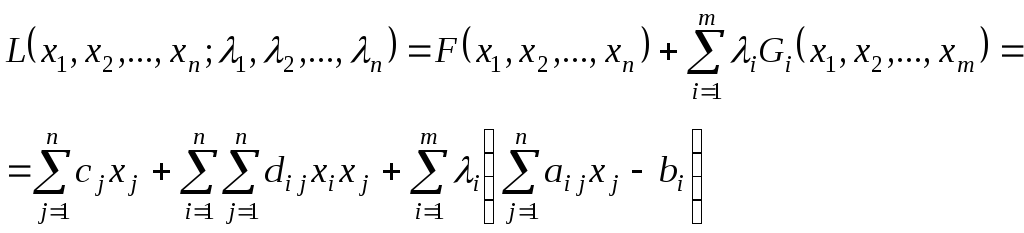 (27)
(27)
![]() (28)
(28)
![]() ,
,
![]() (29)
(29)
В соответствии с обобщенным ММЛ далее необходимо записать условия Куна-Таккера, воспользовавшись теоремой Куна-Таккера:
1)
![]() - условие неотрицательности; (30)
- условие неотрицательности; (30)
![]() ,
,
![]() ;
;
2)
![]() - условие ортогональности; (31)
- условие ортогональности; (31)
![]() ;
;
3)
![]() ; (32)
; (32)
4)
![]() - условие неположительности; (33)
- условие неположительности; (33)
![]() ;
;
5)
![]() ; (34)
; (34)
![]() ;
;
6)
![]() (35)
(35)
Как видно из
выражений (30)-(35), исходная нелинейная
задача КП (25)-(26) с помощью условий
Куна-Таккера представлена как линейная
задача (все вышеуказанные уравнения
содержат переменную
![]() ,
,
![]() линейно). В дальнейшем простые
преобразования позволяют (30)-(35) представить
в виде задачи ЛП и решить ее известным
СМ.
линейно). В дальнейшем простые
преобразования позволяют (30)-(35) представить
в виде задачи ЛП и решить ее известным
СМ.
2.6. О решении задачи НВП методом кусочно-линейной аппроксимации
Этот метод применим
к случаям, когда целевая функция
![]() и функции
и функции
![]() относятся к классу сепарабельных
функций, т.е. функций, представимых в
виде:
относятся к классу сепарабельных
функций, т.е. функций, представимых в
виде:
![]() (36)
(36)
![]() ,
,
![]() (37)
(37)
Задача в этом случае имеет вид:
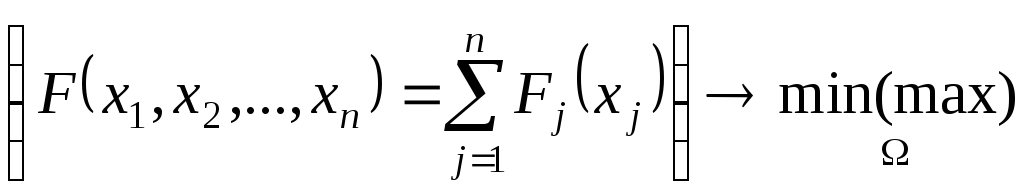 (38)
(38)
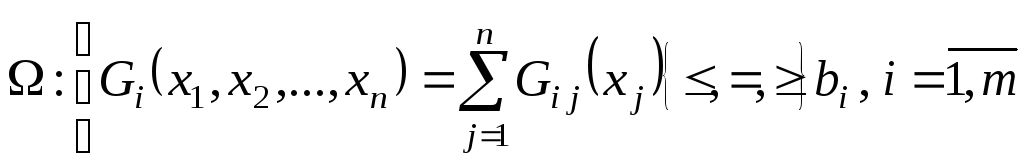 (39)
(39)
Дальнейшая задача
состоит в том, чтобы все функции
![]() ,
,
![]() и
и
![]() аппроксимировать линейными функциями.
Тогда задача (38)-(39) будет представлена
как задача ЛП.
аппроксимировать линейными функциями.
Тогда задача (38)-(39) будет представлена
как задача ЛП.
Пусть функция
![]() - непрерывная функция, заданная на
некотором отрезке
- непрерывная функция, заданная на
некотором отрезке
![]() ,
,
![]() ,
,
![]() ,
тогда имеет место выражение:
,
тогда имеет место выражение:
![]() , (40)
, (40)
где
![]() - линейная функция, аппроксимирующая
непрерывную функцию
- линейная функция, аппроксимирующая
непрерывную функцию
![]() на отрезке
на отрезке
![]() .
.
Если функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() заменить соответственно линейными
функциями в их областях определения,
используя (40), то задача НВП (38)-(39)
преобразуется в задачу ЛП вида:
заменить соответственно линейными
функциями в их областях определения,
используя (40), то задача НВП (38)-(39)
преобразуется в задачу ЛП вида:
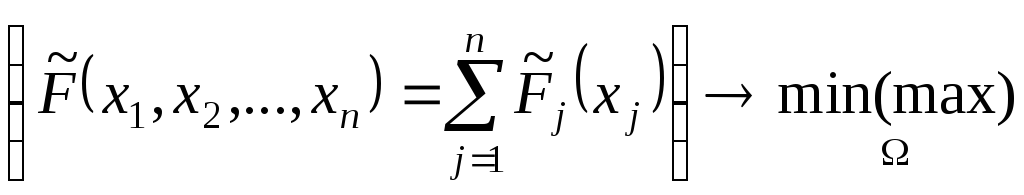 (41)
(41)
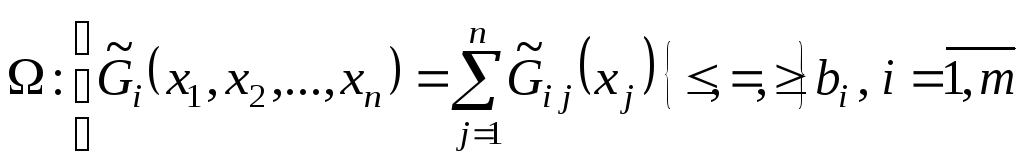 (42)
(42)
![]() - кусочно-линейная
аппроксимация функции
- кусочно-линейная
аппроксимация функции
![]() ,
,
![]() .
.
![]() - кусочно-линейная
аппроксимация функции
- кусочно-линейная
аппроксимация функции
![]() ,
,
![]() .
.
Задача (41)-(42) является задачей ЛП и решается универсальным СМ.
2.7. Метод штрафных функций (МШФ) и метод барьерных функций (МБФ)
Эти методы позволяют исходную задачу нелинейного выпуклого программирования (НВП) преобразовать в последовательность задач безусловной оптимизации, методы решения которых известны.
В МШФ целевая
функция
![]() исходной задачи НВП и ограничений
функции
исходной задачи НВП и ограничений
функции
![]() ,
,
![]() представляется в виде одной обобщенной
функции
представляется в виде одной обобщенной
функции
![]() вида:
вида:
![]() (43)
(43)
где
![]() и называется коэффициентом
штрафа;
и называется коэффициентом
штрафа;
![]() - штрафная
функция,
это непрерывная функция, которая
- штрафная
функция,
это непрерывная функция, которая
удовлетворяет условию:
![]() ,
,
![]() (
(![]() - ОДР задачи НВМ);
- ОДР задачи НВМ);
![]() ,
,
![]()
![]() формируется из
ограничений функций
формируется из
ограничений функций
![]() ,
,
![]() .
.
В МБФ обобщенная
функция
![]() формируется аналогично.
формируется аналогично.
![]() (44)
(44)
где
![]() - барьерный коэффициент;
- барьерный коэффициент;
![]() - непрерывная
функция в области
- непрерывная
функция в области
![]() ,
неограниченно возрастает, когда точка
,
неограниченно возрастает, когда точка
![]() приближается к границе области
приближается к границе области
![]() ;
эта функция образует "барьер",
препятствующий выходу из
;
эта функция образует "барьер",
препятствующий выходу из
![]() .
.
![]() формируется с
помощью функций
формируется с
помощью функций
![]() ,
,
![]() .
.
